محدد
أو المحدد ، - في الرياضيات ، سجل الأرقام في شكل جدول مربع ، وفقًا لذلك يتم وضع رقم آخر ("قيمة" المحدد). في كثير من الأحيان ، يعني مصطلح "محدد" كلاً من معنى المحدد وشكل تدوينه. تجعل المحددات من الممكن كتابة التعبيرات المعقدة التي تظهر بسهولة ، على سبيل المثال ، عند حل المعادلات الخطية في الهندسة التحليلية وفي التحليل الرياضي. يعزى اكتشاف المحددات إلى عالم الرياضيات الياباني S. Kova (1683) ، وبشكل مستقل ، إلى G. Leibniz (1693). تعود النظرية الحديثة إلى أعمال J. Binet و O. Cauchy و C. Jacobi في بداية القرن التاسع عشر. أبسط محدد يتكون من 4 أرقام ، تسمى العناصر ، مرتبة في صفين وعمودين. ويقال أن هذا المحدد من الدرجة الثانية. على سبيل المثال ، هذا هو المحدد

قيمتها 2 * 5 - 3 * 1 (أي 10 - 3 أو 7). في الحالة العامة ، عادة ما يتم كتابة محدد الترتيب الثاني في النموذج

وقيمته هي a1b2 - a2b1 ، حيث a و b أرقام أو وظائف. يتكون محدد الترتيب الثالث من 9 عناصر مرتبة في 3 صفوف و 3 أعمدة. بشكل عام ، يتكون محدد الترتيب n من عناصر n2 ، وعادة ما يتم كتابته كـ

يشير الفهرس الأول لكل عنصر إلى رقم الصف ، ويشير الثاني إلى رقم العمود عند التقاطع الذي يوجد به هذا العنصر ، لذا فإن aij هو عنصر الصف الأول والعمود j. غالبًا ما يتم كتابة هذا المحدد كـ | aij |. إحدى طرق حساب المحددات ، التي تُستخدم دائمًا تقريبًا في حساب محددات الرتبة الأعلى ، هي التوسع في "القاصر". العنصر الثانوي المقابل لأي عنصر من المحددات هو محدد ترتيب أقل من 1 ، يتم الحصول عليه من العنصر الأصلي عن طريق حذف الصف والعمود عند التقاطع الذي يقف عليه هذا العنصر. على سبيل المثال ، القاصر المقابل للعنصر a2 من المحدد

"المكمل الجبري" لعنصر ما هو ثانوي ، يؤخذ بعلامة زائد إذا كان مجموع أرقام الصفوف والأعمدة عند التقاطع الذي يقف عليه العنصر زوجيًا ، ومع علامة الطرح إذا كان فرديًا. في المثال أعلاه ، يوجد العنصر a2 في العمود الأول والصف الثاني ؛ المجموع (1 + 2) فردي ، وبالتالي فإن المكمل الجبري للعنصر a2 يساوي صغره ، مأخوذ بعلامة ناقص ، أي

قيمة المحدد تساوي مجموع حاصل ضرب عناصر أي صف (أو أي عمود) ومكملاتها الجبرية. على سبيل المثال ، المحدد

الموسعة فوق العمود الأول له شكل

والتوسع في الصف الثاني له الشكل

من خلال حساب كل طفيف وضربه في معامل ، من السهل التحقق من أن كلا التعبيرين متماثلان. قيمة المحدد. تحت قيمة المحدد

من المعتاد فهم مجموع كل منتجات n من العناصر ، أي

في هذه الصيغة ، يتم إجراء الجمع على جميع التباديل j1 و ј و jn للأرقام 1 و 2 و ј و n وتوضع علامة الجمع أمام العضو إذا كان التقليب زوجيًا وعلامة ناقص إذا كان هذا التقليب أمر غريب. مثل هذا المجموع ن ​​بالضبط! الأعضاء ، نصفهم مأخوذ بعلامة الجمع ، ونصف - بعلامة الطرح. يحتوي كل مصطلح مجموع على مصطلح واحد من كل عمود وكل صف من المحدد. يمكن إثبات أن هذا المبلغ يتطابق مع التعبير الذي تم الحصول عليه من خلال توسيع المحدد في القصر.
الخصائص المحددة.ومن أهم خصائص المحدد نذكر الآتي. (ط) إذا كانت جميع عناصر أي صف (أو أي عمود) صفراً ، فإن قيمة المحدد تساوي صفرًا أيضًا:

(2) إذا كانت عناصر صفين (أو عمودين) متساوية أو متناسبة ، فإن قيمة المحدد هي صفر:

(3) لا تتغير قيمة المحدد إذا كانت جميع صفوفه وأعمدته متبادلة ، أي اكتب السطر الأول على أنه العمود الأول ، والسطر الثاني في العمود الثاني ، وهكذا. (هذه العملية تسمى التحويل). علي سبيل المثال،

(4) لا تتغير قيمة المحدد إذا أضفنا إلى عناصر صف واحد (أو عمود) العناصر المقابلة لصف آخر (أو عمود) مضروبًا في عامل تعسفي. يضرب المثال التالي عناصر الصف الثاني في -2 ويضيفها إلى عناصر الصف الأول:

(5) إذا تم تبديل صفين (أو عمودين) ، فإن علامة التغييرات المحددة:

(6) إذا كانت جميع عناصر صف واحد (أو عمود واحد) تحتوي على عامل مشترك ، فيمكن عندئذٍ إخراج هذا العامل من علامة المحدد:

مثال. احسب قيمة محدد الترتيب الرابع التالي:

دعنا نضيف السطر الرابع إلى السطر الأول:

اطرح العمود الأول من العمود الرابع:

اضرب العمود الثالث في 3 واطرح من العمود الرابع:

يمكنك تبديل الصفوف والأعمدة إذا أردت:

دعونا نفك المحدد بواسطة عناصر الصف الرابع. ثلاثة عناصر من هذا الصف تساوي صفرًا ، والعنصر غير الصفري موجود في العمود الثالث ، وبما أن المجموع (3 + 4) فردي ، فإن مكمله الجبري له علامة ناقص. نتيجة لذلك ، نحصل على:

يمكن أن يتحلل القاصر إلى عناصر من الصف الثالث: اثنان من عناصره يساوي الصفر ، والعنصر غير الصفري في العمود الثالث ؛ المجموع (3 + 3) متساو ، لذا يمكن متابعة المساواة السابقة:

التطبيقات. حل نظام المعادلات

يمكن الحصول عليها بضرب المعادلة الأولى في b2 ، والثانية في b1 ، ثم طرح معادلة واحدة من الأخرى. من خلال القيام بهذه العمليات ، نحصل على

أو إذا

ومن بعد

مثل هذا السجل للحل بمساعدة المحددات يسمح بالتعميم على حالة حل نظام من المعادلات الخطية n مع n مجهولة ؛ سيكون كل محدد من الترتيب التاسع. محدد نظام المعادلات الخطية

إرادة

لاحظ أنه إذا كانت D = 0 ، فإن المعادلات إما غير متسقة أو غير مستقلة. لذلك ، يسمح لك الحساب الأولي للمحدد D بالتحقق مما إذا كان نظام المعادلات الخطية قابلاً للحل.
المحددات في الهندسة التحليلية.يمكن تمثيل المعادلة العامة للقسم المخروطي كـ

محدد

يسمى المميز. إذا كانت D = 0 ، فإن المنحنى يتدهور إلى زوج من الخطوط المتوازية أو المتقاطعة ، أو إلى نقطة (انظر أيضًا أقسام CONIC). مثال آخر: مساحة المثلث أ مع النقاط عند النقاط (تجاوز - عكس اتجاه عقارب الساعة) (س 1 ، ص 1) ، (س 2 ، ص 2) و (س 3 ، ص 3) تعطى بواسطة

ربط المحددات بالمصفوفات.المصفوفة هي سجل لمصفوفة من الأرقام على شكل جدول مستطيل. المحددات مرتبطة بالمصفوفات المربعة ؛ على سبيل المثال ، محدد المصفوفة

إذا كانت A و B و С عبارة عن مصفوفات مربعة ثم | A | * | B | = | ج |.
أنظر أيضاالجبر هو خلاصة.
يعقوبي.إذا كانت x = f (u ، v) ، y = g (u ، v) هي تحويل إحداثيات ، فإن المحدد

يطلق عليه محدد جاكوبي أو جاكوبي لهذا التحول. إذا كانت J لا تساوي 0 في نقطة ما ، فيمكن حل معادلات التحويل في جوارها بشكل فريد فيما يتعلق بـ u و v ، وتمثيلها كوظائف في x و y.
انظر التحليل الرياضي.

موسوعة كولير. - مجتمع مفتوح. 2000 .

المرادفات:

شاهد ما هو "DETERMINANT" في القواميس الأخرى:

محدد ، محدد ، ذكر. (كتاب). 1. ما يحدد ، يعبر عن شيء ما. 2. كتاب يكون مرجعا في تحديد الشيء (علمي). تحديد النبات. دليل الفطر. 3. عبارة مكوّنة من ... ... القاموس التوضيحي لأوشاكوف

- (محدد) عبارة رياضية مجمعة وفق قاعدة معينة من أرقام n2 ، تستخدم في حل ودراسة أنظمة المعادلات الجبرية من الدرجة الأولى. الرقم ن يسمى ترتيب المحدد. إذن ، محدد الترتيب الثاني ... قاموس موسوعي كبير

المعرف ، الهسه ، القاموس المحدد للمرادفات الروسية. محدد الاسم ، عدد المرادفات: 10 محدد تلقائي (1) ... قاموس مرادف

محدد- (محدد) عبارة رياضية مجمعة وفق قاعدة معينة من أرقام n2 ، تستخدم في حل ودراسة أنظمة المعادلات الجبرية من الدرجة الأولى. الرقم ن يسمى ترتيب المحدد. إذن ، محدد الترتيب الثاني ... موسوعة البوليتكنيك الكبرى

ديتيرمينر ، أنا ، زوجي. 1. جهاز لتحديد ما n. ، وكذلك بشكل عام ، وبمساعدة من الممكن n. تحديد بالضبط. هاتف مع معرف المتصل. يا إيقاع. 2. كتاب للإشارة عند تحديد ما ن. (متخصص.). يا نباتات ... القاموس التوضيحي لأوزيغوف

- (محدد) المصفوفة المربعة A = || aij || طلب n ، detA كثير الحدود ... موسوعة فيزيائية

محدد- - موضوعات الاتصالات والمفاهيم الأساسية EN المحدد ... دليل المترجم الفني

هذا المصطلح له معاني أخرى ، انظر المحدد (المعاني). المحدد (أو المحدد) هو أحد المفاهيم الأساسية للجبر الخطي. محدد المصفوفة هو متعدد الحدود في عناصر المصفوفة المربعة (أي ، y ... ويكيبيديا

محدد- المؤهل 3.4.6 (المساعد): كود الصنف المساعد UDC. مصدر … قاموس - كتاب مرجعي للمصطلحات المعيارية والتقنية

أنا؛ م 1. كتاب. ما يتحدد ، يتحدد بما ل. يمكن أن يكون الصوت عاملاً محددًا للسرعة. المحدد الرئيسي للوقت هو حركة الشمس في الفضاء الخارجي. 2. المواصفات. دليل (كتاب أو جدول) لتحديد ماذا ... ... قاموس موسوعي

كتب

• مفتاح زراعة كاسيات البذور للنباتات الخشبية عن طريق الفاكهة والبذور ، Sinitsyn Evgeny Mikhailovich. المحدد يتكون من جزأين. الجزء الأول هو جدول لتحديد الأجناس ، والثاني يتضمن جداول لتحديد أنواع كاسيات البذور من النباتات الخشبية عن طريق ...

· محدد ميدان المصفوفات A من الترتيب n أو محدد الترتيب n يسمى عددًا يساوي المجموع الجبري ص! الأعضاء ، كل منها منتج صعناصر المصفوفة مأخوذة من كل صف وكل عمود بعلامات معينة. يتم الإشارة إلى المحدد بواسطة أو.

محدد من الدرجة الثانيةهو رقم يتم التعبير عنه على النحو التالي: . علي سبيل المثال .

محدد من الدرجة الثالثةمحسوبة على قاعدة المثلثات (حكم ساروس):.

مثال. .

تعليق. في الممارسة العملية ، تُحسب محددات الترتيب الثالث ، وكذلك الطلبات الأعلى ، باستخدام خصائص المحددات.

خصائص محددات الترتيب التاسع.

1. لن تتغير قيمة المحدد إذا تم استبدال كل صف (عمود) بعمود (صف) بنفس الرقم - تبديل موضع.

2. إذا كان أحد صفوف (عمود) المحدد يتكون من أصفار ، فإن قيمة المحدد تساوي صفرًا.

3. إذا تم تبادل صفين (عمودين) في المحدد ، فلن تتغير القيمة المطلقة للمحدد ، وستتغير العلامة إلى العكس.

4. المحدد الذي يحتوي على صفين متطابقين (عمودين) يساوي صفرًا.

5. يمكن إخراج العامل المشترك لجميع عناصر الصف (العمود) من علامة المحدد.

· تحت السن القانوني بعض عنصر المحدد صالترتيب عشر يسمى المحدد ( ص-1) الترتيب ، الذي تم الحصول عليه من الأصل عن طريق حذف الصف والعمود عند تقاطع العنصر المحدد. تعيين: .

· الجمع الجبري عنصر المحدد يسمى ثانوي ، يؤخذ مع الإشارة. التعيين: هكذا =.

6. محدد المصفوفة المربعة يساوي مجموع حاصل ضرب عناصر أي صف (أو عمود) ومكملاتها الجبرية ( نظرية التحلل).

7. إذا كان كل عنصر في الصف -th هو المجموع كحيث يتم تمثيل المحدد كمجموع كالمحددات التي تكون فيها جميع الصفوف ، باستثناء الصف -th ، هي نفسها كما في المحدد الأصلي ، ويتكون الصف -th في المحدد الأول من المصطلحات الأولى ، في الصف الثاني - من الثاني ، وهكذا. وينطبق الشيء نفسه على الأعمدة.

8. لن يتغير المحدد إذا تمت إضافة صف آخر (عمود) مضروبًا في رقم إلى أحد الصفوف (الأعمدة).

عاقبة. إذا تمت إضافة مجموعة خطية من الصفوف (الأعمدة) الأخرى إلى الصف (العمود) للمحدد ، فلن يتغير المحدد.

9. محدد المصفوفة القطرية يساوي حاصل ضرب العناصر على القطر الرئيسي ، أي

تعليق. محدد المصفوفة المثلثية يساوي أيضًا حاصل ضرب العناصر على القطر الرئيسي.

تجعل الخصائص المدرجة للمحددات من الممكن تبسيط حساباتها بشكل كبير ، وهو أمر مهم بشكل خاص للمحددات عالية الترتيب. في هذه الحالة ، يُنصح بتحويل المصفوفة الأصلية بحيث تحتوي المصفوفة المحولة على صف أو عمود يحتوي على أكبر عدد ممكن من الأصفار (صفوف أو أعمدة "التصفير").

أمثلة.احسب مرة أخرى المحدد المعطى في المثال السابق ، باستخدام خصائص المحددات.

المحلول: لاحظ أنه يوجد في السطر الأول عامل مشترك - 2 ، وفي الثاني - عامل مشترك 3 ، سنخرجهم من علامة المحدد (بواسطة الخاصية 5). بعد ذلك ، نقوم بتوسيع المحدد ، على سبيل المثال ، في العمود الأول ، باستخدام الخاصية 6 (نظرية التوسع).

الأكثر فعالية طريقة لتقليل المحدد إلى شكل قطري أو ثلاثي . لحساب محدد مصفوفة ، يكفي إجراء تحويل للمصفوفة لا يغير المحدد ويجعل من الممكن تحويل المصفوفة إلى قطري.

في الختام ، نلاحظ أنه إذا كان محدد المصفوفة المربعة يساوي صفرًا ، فإن المصفوفة تسمى تتدهور (أو خاص) , غير ذلك - غير منحط .

1. المحدد لا يتغير أثناء التحويل.

2. إذا كان أحد صفوف المحدد يتكون من أصفار ، فإن المحدد يساوي صفرًا.

3. إذا تم إعادة ترتيب صفين في المحدد ، فسيتغير المحدد العلامة.

4. المحدد الذي يحتوي على سلسلتين متماثلتين يساوي صفرًا.

5. إذا تم ضرب جميع عناصر بعض صفوف المحدد في عدد ما ك ، فسيتم ضرب المحدد نفسه في ك.

6. المحدد الذي يحتوي على صفين متناسبين يساوي صفرًا.

7. إذا تم تقديم جميع عناصر الصف الأول من المحدد كمجموع من مصطلحين aij = bj + cj (j =) ، فحينئذٍ يكون المحدد مساويًا لمجموع المحددات ، حيث تكون جميع الصفوف ، باستثناء للصف الأول ، هي نفسها الموجودة في المحدد المحدد ، ويتكون الصف الأول في أحد المجموعات من العناصر bj ، في الآخر - من العناصر cj.

8. لا يتغير المحدد إذا تمت إضافة العناصر المقابلة لصف آخر ، مضروبة في نفس الرقم ، إلى عناصر أحد صفوفه.

تعليق.تظل جميع الخصائص صالحة إذا تم أخذ الأعمدة بدلاً من الصفوف.

تحت السن القانوني M i j للعنصر a i j للمحدد d بالترتيب n هو محدد الترتيب n-1 ، والذي يتم الحصول عليه من d بحذف الصف والعمود اللذين يحتويان على هذا العنصر.

الجمع الجبريالعنصر a i j للمحدد d هو صغره M i j ، مأخوذ بعلامة (-1) i + j. سيتم الإشارة إلى المكمل الجبري للعنصر a i j بواسطة A i j. وهكذا ، A i j = (-1) i + j M i j.

يتم إعطاء طرق الحساب العملي للمحددات بناءً على حقيقة أنه يمكن التعبير عن محدد الترتيب n من حيث محددات الطلبات الأدنى من خلال النظرية التالية.

نظرية (تحلل المحدد في صف أو عمود).

المحدد يساوي مجموع حاصل ضرب كل عناصر صفه التعسفي (أو العمود) ومكملاتها الجبرية. بعبارة أخرى ، هناك تحلل لـ d بدلالة عناصر الصف i-th d = a i 1 A i 1 + a i 2 A i 2 + ... + a i n A i n (i =)

أو العمود j-th d = a 1 j A 1 j + a 2 j A 2 j + ... + a n j A n j (j =).

على وجه الخصوص ، إذا كانت جميع عناصر الصف (أو العمود) باستثناء واحد تساوي الصفر ، فإن المحدد يساوي هذا العنصر مضروبًا في مكمله الجبري.

مثال 1.4.عدم حساب المحدد ، تبين أنها تساوي الصفر. المحلول.اطرح الصف الأول من الصف الثاني ، نحصل على المحدد يساوي الأصل. إذا طرحنا أيضًا الصف الأول من الصف الثالث ، نحصل على المحدد ، حيث يتناسب الصفان. هذا المحدد هو صفر.

مثال 1.5.احسب المحدد د = بتوسيعه بواسطة عناصر العمود الثاني.

المحلول.دعنا نوسع المحدد بواسطة عناصر العمود الثاني:

د = أ 12 أ 12 + أ 22 أ 22 + أ 32 أ 32 =

مثال 1.6.حساب المحدد

أ =
، حيث تكون جميع العناصر الموجودة على أحد جانبي القطر الرئيسي مساوية للصفر. المحلول.لنفكك المحدد أ في الصف الأول: أ = أ 11 أ 11 = . يمكن فك المحدد الموجود على اليمين مرة أخرى على طول السطر الأول ، ثم نحصل على:

أ =
.إلخ. بعد n من الخطوات ، نصل إلى المساواة A = a 11 a 22 ... a nn.

3.المفاهيم الأساسية لأنظمة المعادلات الخطية. نظرية كرامر.

تعريف. نظام المعادلات الخطيةهو اتحاد نالمعادلات الخطية ، كل منها يحتوي على كالمتغيرات. إنه مكتوب على هذا النحو:

يعتقد الكثيرون ، عند مواجهة الجبر العالي لأول مرة ، خطأً أن عدد المعادلات يجب أن يتطابق بالضرورة مع عدد المتغيرات. هذا هو الحال عادة في الجبر المدرسي ، ولكن بالنسبة للجبر العالي ، فهذا غير صحيح بشكل عام.

تعريف. حل نظام المعادلاتعبارة عن سلسلة من الأرقام ( ك 1 ,ك 2 , ..., ك ن) ، وهو حل لكل معادلة في النظام ، أي عند الاستبدال في هذه المعادلة بدلاً من المتغيرات x 1 , x 2 , ..., x نيعطي القيمة الرقمية الصحيحة.

على التوالى، حل نظام المعادلاتيعني العثور على مجموعة حلولها أو إثبات أن هذه المجموعة فارغة. نظرًا لأن عدد المعادلات وعدد المجهول قد لا يكونان متماثلين ، فهناك ثلاث حالات ممكنة:

1. النظام غير متسق ، أي مجموعة كل الحلول فارغة. حالة نادرة إلى حد ما يمكن اكتشافها بسهولة بغض النظر عن طريقة حل النظام.

2. النظام متسق ومحدد ، أي لديه حل واحد بالضبط. النسخة الكلاسيكية المعروفة منذ المدرسة.

3. النظام متوافق وغير محدد ، أي عدد لا نهائي من الحلول. هذا هو الخيار الأصعب. لا يكفي القول بأن "النظام لديه مجموعة لا نهائية من الحلول" - من الضروري وصف كيفية ترتيب هذه المجموعة.

تعريف. عامل س طمسمى مسموح، إذا تم تضمينه في معادلة واحدة فقط من النظام ، ومع معامل 1. بمعنى آخر ، في المعادلات المتبقية ، معامل المتغير س طيجب أن تكون مساوية للصفر.

إذا حددنا متغيرًا واحدًا مسموحًا به في كل معادلة ، فسنحصل على مجموعة من المتغيرات المسموح بها لنظام المعادلات بأكمله. سيتم أيضًا تسمية النظام نفسه ، المكتوب بهذا النموذج ، بالسماح. بشكل عام ، يمكن اختزال نفس النظام الأولي إلى أنظمة مختلفة مسموح بها ، لكن هذا لا يعنينا الآن. فيما يلي أمثلة للأنظمة المسموح بها:

كلا النظامين مسموح بهما فيما يتعلق بالمتغيرات x 1 , x 3 و x 4. ومع ذلك ، مع نفس النجاح ، يمكن القول بأن النظام الثاني مسموح به نسبيًا x 1 , x 3 و xخمسة. يكفي إعادة كتابة المعادلة الأخيرة كـ x 5 = x 4 .

فكر الآن في حالة أكثر عمومية. دعونا نمتلك كل شيء كالمتغيرات منها صمسموح. ثم هناك حالتان ممكنتان:

1. عدد المتغيرات المسموح بها صيساوي العدد الإجمالي للمتغيرات ك: ص = ك. نحصل على النظام من كالمعادلات التي ص = كالمتغيرات المسموح بها. مثل هذا النظام هو تعاوني ومحدد ، لأنه x 1 = ب 1 , x 2 = ب 2 , ..., س ك = ب ك;

2. عدد المتغيرات المسموح بها صأقل من العدد الإجمالي للمتغيرات ك: ص < ك. البقية ( ك − ص) تسمى المتغيرات بالمجان - يمكن أن تأخذ أي قيم يمكن من خلالها حساب المتغيرات المسموح بها بسهولة.

وهكذا ، في الأنظمة المذكورة أعلاه ، المتغيرات x 2 , x 5 , x 6 (للنظام الأول) و x 2 , x 5 (للثاني) أحرار. الحالة عندما تكون هناك متغيرات حرة أفضل صياغة كنظرية ...

كيفية حل؟: - حل نظام المعادلات الخطية باستخدام طريقة الإحلال ("طريقة المدرسة").
- حل النظام عن طريق الجمع (الطرح) لكل مصطلح لمعادلات النظام.
- حل النظام بصيغ كرامر.
- حل النظام باستخدام معكوس المصفوفة.
- حل النظام بطريقة جاوس.

كرامر

أولاً ، ضع في اعتبارك قاعدة كرامر لنظام من معادلتين خطيتين مع مجهولين. هناك أنظمة من المعادلات الخطية بمتغيرين ، وينصح بحلها بالضبط وفقًا لقاعدة كرامر!

ضع في اعتبارك نظام المعادلات

في الخطوة الأولى ، نحسب المحدد ، ويسمى المحدد الرئيسي للنظام.

إذا ، فإن النظام يحتوي على عدد لا نهائي من الحلول أو أنه غير متسق (ليس له حلول). في هذه الحالة ، لن تساعد قاعدة كرامر ، فأنت بحاجة إلى استخدامها طريقة جاوس.

إذا ، إذن النظام لديه حل فريد ، ولإيجاد الجذور علينا حساب محددين آخرين: و

في الممارسة العملية ، يمكن أيضًا الإشارة إلى المؤهلات المذكورة أعلاه بالحرف اللاتيني.

تم العثور على جذور المعادلة بواسطة الصيغ: ،

مثال 7

حل نظام معادلات خطية

نرى أن معاملات المعادلة كبيرة جدًا ، وعلى الجانب الأيمن توجد كسور عشرية بفاصلة. الفاصلة ضيف نادر إلى حد ما في المهام العملية في الرياضيات ؛ لقد أخذت هذا النظام من مشكلة اقتصادية قياسية.

كيف تحل مثل هذا النظام؟ يمكنك محاولة التعبير عن أحد المتغيرات من حيث متغير آخر ، ولكن في هذه الحالة ، ستحصل بالتأكيد على كسور خيالية رهيبة ، والتي من غير الملائم للغاية العمل بها ، وسيبدو تصميم الحل سيئًا. يمكنك ضرب المعادلة الثانية في 6 وطرح حد في حد ، لكن نفس الكسور ستظهر هنا.

ما يجب القيام به؟ في مثل هذه الحالات ، تأتي صيغ كرامر للإنقاذ.

لذا فإن النظام لديه حل فريد.

;

;

كما ترى ، تبين أن الجذور غير عقلانية وتم العثور عليها تقريبًا ، وهو أمر مقبول تمامًا (وحتى شائع) لمشاكل الاقتصاد القياسي.

التعليقات غير مطلوبة هنا ، نظرًا لأن المهمة يتم حلها وفقًا للصيغ الجاهزة ، ومع ذلك ، هناك تحذير واحد. عند استخدام هذه الطريقة ، اجباريجزء المهمة هو الجزء التالي: « ، لذلك فإن النظام لديه حل فريد . خلاف ذلك ، قد يعاقب المراجع على عدم احترام نظرية كرامر.

لن يكون من الضروري التحقق من ذلك ، وهو أمر مناسب للتنفيذ على الآلة الحاسبة: نحن نستبدل القيم التقريبية في الجانب الأيسر من كل معادلة من النظام. نتيجة لذلك ، مع وجود خطأ بسيط ، يجب الحصول على الأرقام الموجودة على الجانب الأيمن.

صيغ كرامر

طريقة كرامر هي التي نجدها على التوالي معرّف النظام الرئيسي(5.3) ، أي محدد المصفوفة أ

و ن المحددات المساعدة D i (i =) ، والتي يتم الحصول عليها من المحدد D عن طريق استبدال العمود i بعمود من الأعضاء الأحرار.

صيغ كرامر لها الشكل:

D × x i = D i (i =). (5.4)

من (5.4) ، تتبع قاعدة كرامر ، والتي تعطي إجابة شاملة لسؤال توافق النظام (5.3): إذا كان المحدد الرئيسي للنظام غير صفري ، فإن النظام لديه حل فريد ، تحدده الصيغ:

إذا كان المحدد الرئيسي للنظام D وجميع المحددات المساعدة D i = 0 (i =) ، فإن النظام يحتوي على عدد لا حصر له من الحلول. إذا كان المحدد الرئيسي للنظام D = 0 ، وكان المحدد الإضافي واحدًا على الأقل مختلفًا عن الصفر ، فهذا يعني أن النظام غير متسق.

المثال 1.14. حل جملة المعادلات باستخدام طريقة كرامر:

س 1 + س 2 + س 3 + س 4 = 5 ، س 1 + 2 س 2 - س 3 + 4 س 4 = -2 ، 2 س 1 - 3 س 2 - س 3 - 5 س 4 = -2 ، 3 س 1 + س 2 + 2x3 + 11x4 = 0.

المحلول.المحدد الرئيسي لهذا النظام د = = -142 ¹ 0 ، لذا فإن النظام لديه حل فريد. دعونا نحسب المحددات المساعدة D i (i =) التي تم الحصول عليها من المحدد D عن طريق استبدال عمود يتكون من معاملات عند x i بعمود من الأعضاء الأحرار: D 1 = = - 142 ، د 2 = = - 284 ، د 3 = = - 426,

D4 = = 142. إذن x 1 = D 1 / D = 1 ، x 2 = D 2 / D = 2 ، x 3 = D 3 / D = 3 ، x 4 = D 4 / D = -1 ، حل النظام هو المتجه C = (1، 2، 3، -1) T.

المفاهيم الأساسية لأنظمة المعادلات الخطية. طريقة جاوس.

أنظر فوق.

طريقة جاوس جوردان(طريقة الحذف الكامل للمجهول) - طريقة تُستخدم لحل الأنظمة التربيعية للمعادلات الجبرية الخطية ، أو إيجاد معكوس المصفوفة ، أو إيجاد إحداثيات متجه في أساس معين ، أو إيجاد رتبة مصفوفة. الطريقة هي تعديل طريقة غاوس.

الخوارزمية

1. حدد العمود الأيسر الأول من المصفوفة ، والذي يحتوي على قيمة واحدة غير صفرية على الأقل.

2. إذا كان أعلى رقم في هذا العمود هو صفر ، فقم بتغيير الصف الأول بالكامل من المصفوفة بصف آخر من المصفوفة ، حيث لا يوجد صفر في هذا العمود.

3. يتم تقسيم جميع عناصر الصف الأول على العنصر العلوي للعمود المحدد.

4. من الصفوف المتبقية ، اطرح الصف الأول ، مضروبًا في العنصر الأول من الصف المقابل ، للحصول على العنصر الأول من كل صف (ما عدا الأول) صفر.

6. بعد تكرار هذا الإجراء مرة واحدة ، يتم الحصول على مصفوفة مثلثة عليا

7. اطرح من الصف قبل الأخير الصف الأخير مضروبًا في المعامل المقابل ، بحيث يبقى الصف قبل الأخير 1 فقط على القطر الرئيسي.

8. كرر الخطوة السابقة للأسطر التالية. نتيجة لذلك ، يتم الحصول على مصفوفة الهوية وحل بدلاً من المتجه الحر (من الضروري إجراء جميع التحويلات نفسها معها).

9. للحصول على المصفوفة المعكوسة ، تحتاج إلى تطبيق جميع العمليات بنفس الترتيب على مصفوفة الوحدة.

طريقة جاوس

تاريخيًا ، الطريقة الأولى والأكثر شيوعًا لحل أنظمة المعادلات الخطية هي طريقة غاوس ، أو طريقة الحذف المتتالي للمجهول. يكمن جوهر هذه الطريقة في حقيقة أنه عن طريق عمليات الحذف المتتالية للمجهول ، يتم تحويل النظام المعطى إلى نظام متدرج (على وجه الخصوص ، مثلث) مكافئ للنظام المعطى. في الحل العملي لنظام المعادلات الخطية بطريقة غاوس ، من الأنسب تقليص الشكل التدريجي ليس نظام المعادلات نفسه ، ولكن المصفوفة الممتدة لهذا النظام ، وإجراء تحويلات أولية على صفوفه. عادة ما تكون المصفوفات التي تم الحصول عليها تباعا أثناء التحويل مرتبطة بعلامة التكافؤ.

مثال 1.13. حل جملة المعادلات باستخدام طريقة جاوس: x + y - 3z = 2، 3x - 2y + z = - 1، 2x + y - 2z = 0.

المحلول.نكتب المصفوفة المعززة لهذا النظام

وقم بإجراء التحويلات الأولية التالية على صفوفه: أ) اطرح الصف الأول من الصفين الثاني والثالث مضروبًا في 3 و 2 على التوالي: ~ ;

ب) اضرب الصف الثالث في (-5) وأضف الثاني إليه: .

نتيجة كل هذه التحولات ، تم تقليل هذا النظام إلى شكل مثلث: x + y - 3z = 2، -5y + 10z = -7، - 10z = 13.

من المعادلة الأخيرة نجد z = -1.3. بالتعويض بهذه القيمة في المعادلة الثانية ، لدينا y = -1.2. بعد المعادلة الأولى نحصل على x = - 0.7

من دفتر الملاحظات:

طريقة جاوس

تتكون الطريقة من جزأين - الأمام والخلف.

تتكون الحركة المباشرة من سلوك توسيع مصفوفة SLE إلى شكل متدرج بمساعدة تحويلات الصف الأولية. في المصفوفة المتدرجة ، يحتوي كل صف لاحق على عدد من الأصفار في البداية أكثر من الصف السابق - أو يكون صفرًا

مثال:

التحويل الأولي لصفوف المصفوفة هو:

1) إضافة أرقام صف واحد من المصفوفة ، مضروبة في عدد ما ، إلى أحد الصفوف السفلية من المصفوفة.

2) تغيير خطين في الأماكن

تتكون الحركة العكسية للطريقة الغاوسية من التعبير المتسلسل لبعض المتغيرات من حيث متغيرات أخرى ، بدءًا من خط الصفر السفلي. والنتيجة هي حل عام.

بعد الحد الأمامي ، هناك 3 خيارات للنوع المتدرج للمصفوفة الموسعة:

1) يحتوي كل سطر تالٍ في البداية على أكثر من صفر واحد بالضبط عن السطر السابق

مثال:

نكتب المعادلة سطرًا سطرًا ونبدأ في العثور على قيمة المتغيرات من المحصلة النهائية.

4X 4 = 8Þ X 4 = 2

عوّض في المعادلة السابقة

2X 3 -3X 4 \ u003d -8 أي 2X 3 -3 * 2 \ u003d -8 أو 2X 3 \ u003d -2 ، Þ X 3 \ u003d -1 ، استبدل X3 و X4 في السطر الثاني ، إلخ. نحصل على الحل الوحيد من SLU

2) عدد الصفوف غير الصفرية أقل من عدد المتغيرات. ثم يحتوي أحد الأسطر في البداية على 2 أصفار على الأقل أكثر من السابق ونعتبر أن السطر اللاحق غير الصفري لا يحتوي على النموذج (0 ... 0 ب) حيث الرقم ب = 0

علي سبيل المثال:

3) آخر سطر غير صفري له الشكل (0… 0 / ب) ، حيث b = 0 يتوافق مع مساواة متناقضة o = b ، وبالتالي فإن النظام غير متوافق

حل SLE بطريقة غاوس

2X 1 + 3X 2 + X 3 \ u003d 1

4 س 1 + 5 س 2 + 4 س 3 = 7

6 × 1 + 10 × 2 - 3 × 3 = -10

نقوم بتكوين المصفوفة الممتدة للحركة المباشرة.

حساب المحددات نالترتيب الثالث:

مفهوم المحدد نالترتيب

باستخدام هذه المقالة حول المحددات ، ستتعلم بالتأكيد كيفية حل مشكلات مثل ما يلي:

حل المعادلة:

والعديد من الأشخاص الآخرين الذين يحب المعلمون ابتكار الكثير.

يلعب محدد المصفوفة أو المحدد دورًا مهمًا في حل أنظمة المعادلات الخطية. بشكل عام ، تم اختراع المحددات لهذا الغرض. نظرًا لأنه غالبًا ما يُقال أيضًا "محدد المصفوفة" ، فسنذكر المصفوفات هنا أيضًا. المصفوفةهو جدول مستطيل مكون من أرقام لا يمكن تبادلها. المصفوفة المربعة هي جدول يحتوي على نفس عدد الصفوف والأعمدة. فقط المصفوفة المربعة يمكن أن يكون لها محدد.

من السهل فهم منطق كتابة المحددات وفق المخطط التالي. لنأخذ نظامًا من معادلتين مع مجهولين مألوفين لك من المدرسة:

في المحدد ، تتم كتابة معاملات المجهول بالتسلسل: في السطر الأول - من المعادلة الأولى ، في السطر الثاني - من المعادلة الثانية:

على سبيل المثال ، إذا أعطيت نظام المعادلات

ثم يتم تكوين المحدد التالي من معاملات المجهول:

لنفترض أن لدينا جدولًا مربعًا يتكون من أعداد مرتبة نالصفوف (الصفوف الأفقية) وفي نأعمدة (صفوف عمودية). بمساعدة هذه الأرقام ، وفقًا لبعض القواعد التي سندرسها أدناه ، وجدوا رقمًا يسمونه محدد نالترتيب عشر ويشار إليها على النحو التالي:

(1)

يتم استدعاء الأرقام عناصرالمحدد (1) (الفهرس الأول يعني رقم الصف ، والثاني - رقم العمود ، الذي يوجد عند تقاطعه عنصر ؛ أنا = 1, 2, ..., ن؛ ي= 1 ، 2 ، ... ، ن). ترتيب المحدد هو عدد صفوفه وأعمدته.

خط مستقيم وهمي يربط بين عناصر المحدد الذي يكون كلا المؤشرين متماثلين فيه ، أي عناصر

مسمى قطري رئيسي، القطر الآخر هو الجانب.

حساب المحددات من الدرجة الثانية والثالثة

دعونا نوضح كيف يتم حساب محددات الطلبات الثلاثة الأولى.

محدد الترتيب الأول هو العنصر نفسه ، أي

محدد الترتيب الثاني هو الرقم الذي تم الحصول عليه على النحو التالي:

, (2)

حاصل ضرب العناصر في القطرين الرئيسي والثانوي ، على التوالي.

تُظهر المساواة (2) أن ناتج عناصر القطر الرئيسي مأخوذ بعلامة ، وأن حاصل ضرب عناصر القطر الثانوي يؤخذ بعلامة معاكسة .

مثال 1احسب محددات الدرجة الثانية:

المحلول. بالصيغة (2) نجد:

محدد الترتيب الثالث هو رقم تم الحصول عليه مثل هذا:

(3)

من الصعب تذكر هذه الصيغة. ومع ذلك ، هناك قاعدة بسيطة تسمى حكم المثلث ، مما يجعل من السهل إعادة إنتاج التعبير (3). للدلالة على عناصر المحدد بالنقاط ، فإننا نربطها بواسطة مقاطع الخط المستقيم تلك التي تعطي منتجات عناصر المحدد (الشكل 1).

توضح الصيغة (3) أن منتجات عناصر القطر الرئيسي ، وكذلك العناصر الموجودة عند رؤوس مثلثين ، قواعدهما متوازية ، تؤخذ مع علاماتها ؛ مع العناصر المقابلة - منتجات عناصر القطر الثانوي ، وكذلك العناصر الموجودة عند رؤوس مثلثين متوازيين .

في الشكل 1 ، تم تمييز القطر الرئيسي وقواعد المثلثات المقابلة له والقطري الثانوي وقواعد المثلثات المقابلة له باللون الأحمر.

عند حساب المحددات ، من المهم جدًا ، كما هو الحال في المدرسة الثانوية ، أن تتذكر أن ضرب رقم ناقص في رقم سالب ينتج عنه علامة زائد ، وعلامة زائد مضروبة في رقم سالب ينتج عنها رقم بعلامة ناقص.

مثال 2احسب محدد الترتيب الثالث:

المحلول. باستخدام قاعدة المثلثات ، نحصل على

حساب المحددات نالترتيب

توسيع الصف أو العمود للمحدد

لحساب المحدد نالترتيب ، من الضروري معرفة واستخدام النظرية التالية.

نظرية لابلاس.المحدد يساوي مجموع حاصل ضرب عناصر أي صف ومكملاتها الجبرية ، أي

تعريف. إذا كان في المحدد نالترتيب اختيار تعسفيا صخطوط و صأعمدة ( ص < ن) ، فإن العناصر الموجودة عند تقاطع هذه الصفوف والأعمدة تشكل مصفوفة ترتيب.

محدد هذه المصفوفة يسمى تحت السن القانوني المحدد الأصلي. على سبيل المثال ، ضع في اعتبارك المحدد:

لنقم ببناء مصفوفة من الصفوف والأعمدة ذات الأرقام الزوجية:

محدد

مسمى تحت السن القانونيمحدد. حصل على قاصر من الدرجة الثانية. من الواضح أنه يمكن بناء قاصرين مختلفين من الرتب الأولى والثانية والثالثة من.

إذا أخذنا عنصرًا وشطبنا الصف والعمود عند تقاطعهما في المحدد ، فسنحصل على عنصر ثانوي يسمى العنصر الأصغر ، والذي نشير إليه بـ:

.

إذا تم ضرب القاصر في ، حيث 3 + 2 هو مجموع أرقام الصفوف والأعمدة عند التقاطع الذي يقف عليه العنصر ، فإن المنتج الناتج يسمى إضافة جبريةعنصر ويشار إليه ،

بشكل عام ، سيتم الإشارة إلى العنصر الصغير للعنصر ، والمكمل الجبري بـ ،

(4)

على سبيل المثال ، لنحسب المكملات الجبرية للعناصر ومحدد الترتيب الثالث:

بالصيغة (4) نحصل عليها

عند تحليل المحدد ، غالبًا ما يتم استخدام الخاصية التالية للمُحدد نالترتيب الثالث:

إذا تمت إضافة منتج العناصر المقابلة لصف أو عمود آخر بواسطة عامل ثابت إلى عناصر أي صف أو عمود ، فلن تتغير قيمة المحدد.

مثال 4

دعونا نطرح مبدئيًا عناصر الصف الرابع من الصفين الأول والثالث ، ثم لدينا

في العمود الرابع من المحدد الذي تم الحصول عليه ، ثلاثة عناصر هي أصفار. لذلك ، من الأفضل توسيع هذا المحدد بواسطة عناصر العمود الرابع ، لأن المنتجات الثلاثة الأولى ستكون صفرًا. لهذا السبب

يمكنك التحقق من الحل باستخدام حاسبة محدد على الإنترنت .

ويوضح المثال التالي كيف يمكن اختزال حساب المحدد لأي ترتيب (في هذه الحالة ، الرابع) إلى حساب المحدد من الدرجة الثانية.

مثال 5احسب المحدد:

دعونا نطرح عناصر الصف الأول من الصف الثالث ، ونضيف عناصر الصف الأول إلى عناصر الصف الرابع ، ثم نحصل على

في العمود الأول ، تكون جميع العناصر باستثناء العنصر الأول أصفارًا. بمعنى ، يمكن أن يتحلل المحدد بالفعل في العمود الأول. لكننا في الحقيقة لا نريد حساب المحدد من الرتبة الثالثة. لذلك ، سنقوم بإجراء المزيد من التحولات: إلى عناصر الصف الثالث نضيف عناصر الصف الثاني ، مضروبًا في 2 ، ومن عناصر الصف الرابع نطرح عناصر الصف الثاني. نتيجة لذلك ، يمكن توسيع المحدد ، وهو مكمل جبري ، في العمود الأول ، وسيتعين علينا فقط حساب المحدد من الدرجة الثانية وعدم الخلط بين العلامات:

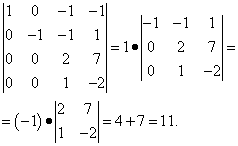
تحويل المحدد إلى شكل مثلث

المحدد الذي تكون فيه جميع العناصر الموجودة على جانب واحد من أحد الأقطار تساوي صفرًا يسمى المثلث. يتم تقليل حالة القطر الثانوي إلى حالة القطر الرئيسي عن طريق عكس ترتيب الصفوف أو الأعمدة. مثل هذا المحدد يساوي منتج عناصر القطر الرئيسي.

للتصغير إلى شكل مثلث ، يتم استخدام نفس خاصية المحدد نالترتيب الذي استخدمناه في الفقرة السابقة: إذا أضفنا منتج العناصر المقابلة لصف أو عمود آخر بواسطة عامل ثابت إلى عناصر أي صف أو عمود ، فلن تتغير قيمة المحدد.

يمكنك التحقق من الحل باستخدام حاسبة محدد على الإنترنت .

الخصائص المحددة نالترتيب

في الفقرتين السابقتين ، استخدمنا بالفعل إحدى خصائص المحدد نالترتيب. في بعض الحالات ، لتبسيط حساب المحدد ، يمكنك استخدام خصائص مهمة أخرى للمُحدد. على سبيل المثال ، يمكن للمرء أن يختزل المحدد إلى مجموع اثنين من المحددات ، يمكن توسيع أحدهما أو كليهما بسهولة على طول صف أو عمود ما. هناك الكثير من حالات هذا التبسيط ، ويجب تحديد مسألة استخدام خاصية أو أخرى للمُحدد بشكل فردي.

محدد المصفوفة (محدد المصفوفة) هو جدول مربّع من الأرقام أو الرموز الرياضية ( Δ د).

تعريف. محدد المصفوفة ن × نهو الرقم:

أين ( α 1، α 2، ...، α n) - تبديل الأرقام من 1 قبل ن, N (α 1، α 2، ...، α n)- عدد الانعكاسات في التقليب ، يحدث الجمع على كل التباديل الممكنة للترتيب ن.

محدد المصفوفة أيشار إليها أساسًا باسم دي تي (أ) ، | أ |، أو ؟(أ).

المعلمات ، بمساعدة حل جميع أنواع المصفوفات الجبرية.

ل أوجد محدد المصفوفةمن الضروري معرفة الخصائص الأساسية للمصفوفات وتسلسل الإجراءات عند حل المصفوفة.

1. لمصفوفات النظام ن = 2تم إيجاد المحدد باستخدام الصيغة: Δ= أ 11 *أ 22-أ 12 *أ 21
2. لمصفوفات النظام ن = 3تم إيجاد المحدد من خلال الجمع الجبري أو باستخدام طريقة Sarrus.
3. تتحلل مصفوفة ذات أبعاد أكبر من 3 إلى إضافات جبرية ، تم العثور على محدداتها (الصغار). على سبيل المثال ، يتم حساب محدد مصفوفة من الدرجة الرابعة من خلال التوسع في الصفوف أو الأعمدة.

بالنسبة إيجاد محدد المصفوفة، التي تحتوي على وظائف في المصفوفة ، يتم استخدام الطرق القياسية. على سبيل المثال ، لإيجاد محدد مصفوفة من الرتبة الثالثة:

دعنا نستخدم التوسع في السطر الأول:

Δ = sin (x) × + 1 × = 2sin (x) cos (x) - 2cos (x) = sin (2x) - 2cos (x)

احسب محدد المصفوفة.

احسب محدد المصفوفةهناك عدة طرق مذكورة أدناه.

الطريقة الأكثر شيوعًا لحساب محدد المصفوفة هي طريقة اختيار الإضافات الجبرية. هناك نسخة أبسط من هذه الطريقة - حساب المحدد باستخدام قاعدة Sarrus. تختلف هذه الطرق عند حساب محدد مصفوفة صغيرة بسيطة ، وإذا كنت بحاجة إلى حساب مصفوفة ذات أبعاد كبيرة ، فعندئذٍ مثل طرق حساب محدد المصفوفة:

• حساب المحدد بطريقة تخفيض الأمر ،
• حساب المحدد بطريقة غاوس (عن طريق تقليل المصفوفة إلى شكل مثلث) ،
• حساب المحدد بطريقة التحلل.

في Excel ، لحساب المحدد ، يتم استخدام الوظيفة = MOPRED (نطاق الخلايا).