URČUJÍCÍ
neboli determinant, - v matematice záznam čísel ve formě čtvercové tabulky, podle které se klade jiné číslo ("hodnota" determinantu). Velmi často se pod pojmem „determinant“ rozumí jak význam determinantu, tak i forma jeho zápisu. Determinanty umožňují pohodlně psát složité výrazy, které vznikají např. při řešení lineárních rovnic v analytické geometrii a v matematické analýze. Objev determinantů je připisován japonskému matematikovi S. Kovovi (1683) a nezávisle také G. Leibnizovi (1693). Moderní teorie sahá až k pracím J. Bineta, O. Cauchyho a C. Jacobiho na počátku 19. století. Nejjednodušší determinant se skládá ze 4 čísel, nazývaných prvky, uspořádaných do 2 řad a 2 sloupců. O takovém determinantu se říká, že je 2. řádu. Například toto je určující
Jeho hodnota je 2*5 - 3*1 (tj. 10 - 3 nebo 7). V obecném případě se determinant 2. řádu obvykle zapisuje do tvaru
A jeho hodnota je a1b2 - a2b1, kde a a b jsou čísla nebo funkce. Determinant 3. řádu se skládá z 9 prvků uspořádaných do 3 řad a 3 sloupců. Obecně se determinant n-tého řádu skládá z n2 prvků a obvykle se zapisuje jako
První index každého prvku udává číslo řádku, druhý - číslo sloupce, na jehož průsečíku se tento prvek nachází, takže aij je prvek i-tého řádku a j-tého sloupce. Často se takový determinant zapisuje jako |aij|. Jednou z metod výpočtu determinantu, téměř vždy používanou při výpočtu determinant vyššího řádu, je rozšiřování v „minorech“. Menší odpovídající libovolnému prvku determinantu je determinant řádu menší než 1, získaný z původního vymazáním řádku a sloupce, na jejichž průsečíku tento prvek stojí. Například moll odpovídající prvku a2 z determinantu
„Algebraickým doplňkem“ prvku je jeho moll, braný se znaménkem plus, pokud je součet čísel řádků a sloupců, na jejichž průsečíku prvek stojí, sudý, a se znaménkem mínus, pokud je lichý. Ve výše uvedeném příkladu je prvek a2 v 1. sloupci a ve 2. řádku; součet (1 + 2) je lichý, a proto je algebraický doplněk prvku a2 roven jeho moll, braný se znaménkem mínus, tzn.
Hodnota determinantu je rovna součtu součinů prvků libovolného řádku (nebo libovolného sloupce) a jejich algebraických doplňků. Například determinant
rozšířený přes první sloupec má tvar
a jeho rozšíření ve druhé řadě má podobu
Výpočtem každého moll a jeho vynásobením koeficientem lze snadno ověřit, že oba výrazy jsou stejné. Hodnota determinantu. Pod hodnotou determinantu
Je zvykem chápat součet všech součinů n prvků, tzn.
V tomto vzorci se sumace provádí přes všechny permutace j1, ј, jn čísel 1, 2, ј, n a před členem je znaménko plus, pokud je permutace sudá, a znaménko mínus, pokud je tato permutace lichá. . Takový součet tvoří přesně n! členů, z nichž polovina je brána se znaménkem plus, polovina - se znaménkem mínus. Každý součtový člen obsahuje jeden člen z každého sloupce a každého řádku determinantu. Lze dokázat, že tento součet se shoduje s výrazem získaným rozšířením determinantu u nezletilých.
Determinantní vlastnosti. Mezi nejdůležitější vlastnosti determinantu uvádíme následující. (i) Pokud jsou všechny prvky libovolného řádku (nebo libovolného sloupce) nulové, pak je hodnota determinantu také nula:
(ii) Pokud jsou prvky dvou řádků (nebo dvou sloupců) stejné nebo úměrné, pak je hodnota determinantu nula:
(iii) Hodnota determinantu se nemění, pokud jsou zaměněny všechny jeho řádky a sloupce, tzn. napište první řádek jako první sloupec, druhý řádek jako druhý sloupec a tak dále. (tato operace se nazývá transpozice). Například,
(iv) Hodnota determinantu se nezmění, pokud k prvkům jednoho řádku (nebo sloupce) přičteme odpovídající prvky jiného řádku (nebo sloupce) vynásobené libovolným faktorem. Následující příklad vynásobí prvky druhého řádku -2 a přidá je k prvkům prvního řádku:
(v) Pokud jsou dva řádky (nebo dva sloupce) prohozeny, determinant změní znaménko:
(vi) Pokud všechny prvky jednoho řádku (nebo jednoho sloupce) obsahují společný faktor, pak lze tento faktor vyjmout ze znaménka determinantu:
Příklad. Vypočítejte hodnotu následujícího determinantu 4. řádu:
K prvnímu řádku přidáme 4. řádek:
Odečtěte 1. sloupec od 4. sloupce:
Vynásobte 3. sloupec 3 a odečtěte od 4. sloupce:
Pokud chcete, můžete zaměnit řádky a sloupce:
Rozšiřme determinant o prvky čtvrté řady. Tři prvky tohoto řádku se rovnají nule, nenulový prvek je ve třetím sloupci, a protože součet (3 + 4) je lichý, má jeho algebraický doplněk znaménko mínus. V důsledku toho získáme:
Vedlejší prvek lze rozložit na prvky třetího řádku: dva jeho prvky se rovnají nule a nenulový prvek je ve třetím sloupci; součet (3 + 3) je sudý, takže lze pokračovat v předchozí rovnosti:
Aplikace. Řešení soustavy rovnic
lze získat vynásobením první rovnice b2, druhé b1 a následným odečtením jedné rovnice od druhé. Provedením těchto operací dostaneme
Nebo když
pak
Takový záznam řešení pomocí determinantů umožňuje zobecnění na případ řešení soustavy n lineárních rovnic s n neznámými; každý determinant bude n-tého řádu. Determinant soustavy lineárních rovnic
vůle
Všimněte si, že pokud D = 0, pak rovnice jsou buď nekonzistentní, nebo nejsou nezávislé. Předběžný výpočet determinantu D tedy umožňuje ověřit, zda je soustava lineárních rovnic řešitelná.
Determinanty v analytické geometrii. Obecná rovnice kuželosečky může být reprezentována jako
Determinant
se nazývá diskriminant. Je-li D = 0, pak křivka degeneruje do dvojice rovnoběžných nebo protínajících se čar nebo do bodu (viz také KUŽELÍSKY). Další příklad: oblast trojúhelníku A s vrcholy v bodech (obtok - proti směru hodinových ručiček) (x1, y1), (x2, y2) a (x3, y3) je dána vztahem
Spojení determinantů s maticemi. Matice je záznam pole čísel ve formě obdélníkové tabulky. Determinanty souvisí se čtvercovými maticemi; například maticový determinant
Jestliže A, B a С jsou čtvercové matice a pak |A|*|B| = |C|.
viz také ALGEBRA JE ABSTRAKTNÍ.
jakobiánský. Jestliže x = f (u, v), y = g (u, v) je transformace souřadnic, pak determinant
Říká se tomu jakobiánský nebo jakobiovský determinant této transformace. Pokud se J v určitém bodě nerovná 0, pak v jeho okolí lze jednoznačně řešit transformační rovnice s ohledem na u a v, které je reprezentují jako funkce x a y.
Viz MATEMATICKÁ ANALÝZA.
Collierova encyklopedie. - Otevřená společnost. 2000 .
Synonyma:Podívejte se, co je „DETERMINANT“ v jiných slovnících:
DETERMINER, determinant, male. (rezervovat). 1. To, co něco určuje, vyjadřuje. 2. Kniha, která slouží jako reference při určování něčeho (vědeckého). Identifikace rostlin. Průvodce houbami. 3. Výraz složený z ... ... Vysvětlující slovník Ushakova
- (determinant) matematický výraz sestavený podle určitého pravidla z n2 čísel, používaný při řešení a studiu soustav algebraických rovnic 1. stupně. Číslo n se nazývá řád determinantu. Takže determinant 2. řádu... Velký encyklopedický slovník
Identifikátor, hesián, moll, determinant Slovník ruských synonym. determinant podstatného jména, počet synonym: 10 autodeterminer (1) … Slovník synonym
URČUJÍCÍ- (determinant) matematický výraz sestavený podle určitého pravidla z n2 čísel, používaný při řešení a studiu soustav algebraických rovnic 1. stupně. Číslo n se nazývá řád determinantu. Takže determinant 2. řádu... Velká polytechnická encyklopedie
DETERMINER, já, manžel. 1. Zařízení k určování jaké n., jakož i obecně, s jehož pomocí lze n. přesně určit. Telefon s ID volajícího. O. rytmus. 2. Kniha pro referenci při určování toho, co n. (specialista.). O. rostliny ... Vysvětlující slovník Ozhegov
- (determinant) čtvercové matice A = ||aij|| řád n, polynom detA … Fyzická encyklopedie
determinant- - Telekomunikační témata, základní pojmy EN determinant ... Technická příručka překladatele
Tento termín má další významy, viz Determinant (významy). Determinant (neboli determinant) je jedním ze základních pojmů lineární algebry. Maticový determinant je polynom v prvcích čtvercové matice (tedy takový, že y ... Wikipedia
determinant- 3.4.6 kvalifikátor (pomocný): Kód pomocné třídy UDC. Zdroj … Slovník-příručka termínů normativní a technické dokumentace
I; m. 1. Kniha. Co je určeno, je určeno tím, co l. Zvuk může být určujícím faktorem rychlosti. Hlavním determinantem času je pohyb Slunce ve vesmíru. 2. Spec. Průvodce (kniha nebo tabulka), který určí, co ... ... encyklopedický slovník
knihy
- Klíč k krytosemenným rostlinám podle plodů a semen, Sinitsyn Evgeny Michajlovič. Determinant se skládá ze dvou částí. První část je tabulka pro identifikaci rodů a druhá obsahuje tabulky pro identifikaci druhů krytosemenných dřevin podle ...
· determinant náměstí matice A n-tého řádu nebo determinant n-tého řádu volalo číslo rovné algebraickému součtu P! členů, z nichž každý je produktem P prvky matice převzaty jeden z každého řádku a každého sloupce s určitými znaky. Determinant se značí nebo .
Determinant druhého řádu je číslo vyjádřené takto: 
. Například 
.
Determinant třetího řádu počítáno podle pravidla trojúhelníků (Sarrusovo pravidlo): .
Příklad. .
Komentář. V praxi se determinanty třetího řádu, stejně jako vyšší řády, počítají pomocí vlastností determinantů.
Vlastnosti determinantů n-tého řádu.
1. Hodnota determinantu se nezmění, pokud bude každý řádek (sloupec) nahrazen sloupcem (řádkem) se stejným číslem - přemístit.
2. Pokud se jeden z řádků (sloupců) determinantu skládá z nul, pak je hodnota determinantu nulová.
3. Pokud se v determinantu zamění dva řádky (sloupce), pak se absolutní hodnota determinantu nezmění a znaménko se změní na opačné.
4. Determinant obsahující dva stejné řádky (sloupce) je roven nule.
5. Společný činitel všech prvků řádku (sloupce) lze vyjmout ze znaménka determinantu.
· Méně důležitý nějaký prvek determinantu Přád se nazývá determinant ( P-1)-tý řád, získaný z originálu smazáním řádku a sloupce, na jehož průsečíku se nachází vybraný prvek. Označení: .
· Algebraické sčítání prvek determinantu se nazývá jeho moll, braný se znaménkem . Označení: Tak =.
6. Determinant čtvercové matice se rovná součtu součinů prvků libovolného řádku (nebo sloupce) a jejich algebraických doplňků ( rozkladová věta).
7. Je-li každý prvek -tého řádku součtem kčleny, pak je determinant reprezentován jako součet k determinanty, ve kterých jsou všechny řádky kromě -té řady stejné jako v původním determinantu, a -tý řádek v prvním determinantu se skládá z prvních členů, ve druhém - z druhého atd. Totéž platí pro sloupce.
8. Determinant se nezmění, pokud se do jednoho z řádků (sloupců) přidá další řádek (sloupec) vynásobený číslem.
Následek. Pokud se k řádku (sloupci) determinantu přidá lineární kombinace jeho dalších řádků (sloupců), pak se determinant nezmění.
9. Determinant diagonální matice je roven součinu prvků na hlavní diagonále, tzn.
Komentář. Determinant trojúhelníkové matice se také rovná součinu prvků na hlavní diagonále.
Uvedené vlastnosti determinantů umožňují výrazně zjednodušit jejich výpočet, což je důležité zejména u determinantů vysokého řádu. V tomto případě je vhodné původní matici transformovat tak, aby transformovaná matice měla řádek nebo sloupec obsahující co nejvíce nul („nulování“ řádků nebo sloupců).
Příklady. Vypočítejte znovu determinant uvedený v předchozím příkladu pomocí vlastností determinantů.
Řešení: Všimněte si, že v prvním řádku je společný faktor - 2 a ve druhém - společný faktor 3, vyjmeme je ze znaménka determinantu (vlastností 5). Dále rozšíříme determinant např. v prvním sloupci pomocí vlastnosti 6 (teorém o rozšíření).
Nejefektivnější způsob redukce determinantu na diagonální nebo trojúhelníkový tvar . Pro výpočet determinantu matice stačí provést transformaci matice, která nemění determinant a umožňuje převést matici na diagonální.
Na závěr poznamenáváme, že pokud je determinant čtvercové matice roven nule, pak se matice nazývá degenerovat (nebo speciální) , v opačném případě - nedegenerované .
1. Determinant se během transpozice nemění.
2. Pokud se jeden z řádků determinantu skládá z nul, pak je determinant roven nule.
3. Pokud jsou v determinantu přeskupeny dva řádky, determinant změní znaménko.
4. Determinant obsahující dva stejné řetězce je roven nule.
5. Pokud jsou všechny prvky některého řádku determinantu vynásobeny nějakým číslem k, pak bude samotný determinant vynásoben k.
6. Determinant obsahující dva proporcionální řádky je roven nule.
7. Jsou-li všechny prvky i-tého řádku determinantu uvedeny jako součet dvou členů aij = bj + cj (j= ), pak je determinant roven součtu determinantů, ve kterém jsou všechny řádky kromě pro i-tý řádek jsou stejné jako v daném determinantu a i-tý řádek v jednom ze sčítanců sestává z prvků bj , ve druhém - z prvků cj .
8. Determinant se nezmění, pokud se k prvkům jednoho z jeho řádků přidají odpovídající prvky jiného řádku, vynásobené stejným číslem.
Komentář. Všechny vlastnosti zůstávají platné, pokud se místo řádků použijí sloupce.
Méně důležitý M i j prvku a i j determinantu d n-tého řádu je determinant řádu n-1, který se získá z d vymazáním řádku a sloupce obsahujícího tento prvek.
Algebraické sčítání prvek a i j determinantu d je jeho vedlejší M i j , braný se znaménkem (-1) i + j . Algebraický doplněk prvku a i j budeme označovat A i j . Tedy A i j = (-1) i + j M i j.
Metody pro praktický výpočet determinantů založené na skutečnosti, že determinant řádu n lze vyjádřit pomocí determinantů nižších řádů, jsou dány následující větou.
Teorém (rozklad determinantu v řádku nebo sloupci).
Determinant je roven součtu součinů všech prvků jeho libovolného řádku (nebo sloupce) a jejich algebraických doplňků. Jinými slovy, dochází k rozkladu d z hlediska prvků i-té řady d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = )
nebo j-tý sloupec d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).
Konkrétně, pokud jsou všechny prvky řádku (nebo sloupce) kromě jednoho rovny nule, pak je determinant roven tomuto prvku vynásobenému jeho algebraickým doplňkem.
Příklad 1.4. Nepočítám determinant 
, ukažte, že se rovná nule. Řešení. Odečteme první řádek od druhého řádku, dostaneme determinant 
rovna originálu. Odečteme-li také první řadu od třetí řady, dostaneme determinant 
, ve kterém jsou dva řádky proporcionální. Tento determinant je nulový.
Příklad 1.5. Vypočítejte determinant D = 
, rozšiřující jej o prvky druhého sloupce.
Řešení. Rozšiřme determinant o prvky druhého sloupce:
D = a 12 A 12 + a 22 A 22 + a 32 A 32 =
Příklad 1.6. Vypočítat determinant
A= 
, ve kterém jsou všechny prvky na jedné straně hlavní diagonály rovny nule. Řešení. Rozšiřme determinant A v prvním řádku: A = a 11 A 11 = 
. Determinant napravo lze znovu rozšířit podél prvního řádku, pak dostaneme:
A= 
.Atd. Po n krocích dospějeme k rovnosti A = a 11 a 22... a nn.
3.Základní pojmy soustav lineárních rovnic. Cramerův teorém.
Definice. Systém lineárních rovnic je spojením n lineární rovnice, z nichž každá obsahuje k proměnné. Píše se to takto:
Mnozí, když se poprvé setkají s vyšší algebrou, se mylně domnívají, že počet rovnic se musí nutně shodovat s počtem proměnných. Ve školní algebře to tak obvykle je, ale pro vyšší algebru to obecně řečeno neplatí.
Definice. Řešení soustavy rovnic je posloupnost čísel ( k 1 ,k 2 , ..., k n), což je řešení každé rovnice soustavy, tzn. při dosazování do této rovnice místo proměnných X 1 , X 2 , ..., x n dává správnou číselnou hodnotu.
resp. řešit soustavu rovnic znamená najít množinu všech jejích řešení nebo dokázat, že tato množina je prázdná. Protože počet rovnic a počet neznámých nemusí být stejný, jsou možné tři případy:
1. Systém je nekonzistentní, tzn. množina všech řešení je prázdná. Poměrně vzácný případ, který lze snadno zjistit bez ohledu na to, jakou metodou systém vyřešit.
2. Systém je konzistentní a definovaný, tzn. má přesně jedno řešení. Klasická verze, známá již ze školy.
3. Systém je kompatibilní a není definován, tzn. má nekonečně mnoho řešení. Toto je nejtěžší možnost. Nestačí konstatovat, že „systém má nekonečnou množinu řešení“ – je třeba popsat, jak je tato množina uspořádána.
Definice. Variabilní x i volala povoleno, pokud je obsažena pouze v jedné rovnici soustavy, a s koeficientem 1. Jinými slovy, ve zbývajících rovnicích je koeficient proměnné x i by se měla rovnat nule.
Pokud v každé rovnici vybereme jednu povolenou proměnnou, získáme sadu povolených proměnných pro celý systém rovnic. Samotný systém, napsaný v této podobě, bude také nazýván povoleným. Obecně řečeno, jeden a tentýž výchozí systém lze redukovat na různé povolené systémy, ale to se nás nyní netýká. Zde jsou příklady povolených systémů:
Oba systémy jsou povoleny s ohledem na proměnné X 1 , X 3 a X 4. Se stejným úspěchem však lze tvrdit, že druhý systém je povolen relativně X 1 , X 3 a X Pět . Poslední rovnici stačí přepsat jako X 5 = X 4 .
Nyní zvažte obecnější případ. Ať máme všechno k proměnné, z toho r jsou povoleny. Pak jsou možné dva případy:
1. Počet povolených proměnných r rovná se celkovému počtu proměnných k: r = k. Získáváme systém z k rovnice, ve kterých r = k povolené proměnné. Takový systém je kolaborativní a určitý, protože X 1 = b 1 , X 2 = b 2 , ..., x k = b k;
2. Počet povolených proměnných r menší než celkový počet proměnných k: r < k. Zbytek ( k − r) proměnné se nazývají volné - mohou nabývat jakýchkoli hodnot, ze kterých lze snadno vypočítat povolené proměnné.
Tedy ve výše uvedených systémech proměnné X 2 , X 5 , X 6 (pro první systém) a X 2 , X 5 (za druhé) jsou zdarma. Případ, kdy jsou volné proměnné, je lépe formulovat jako věta...
Jak vyřešit?: – Řešení soustavy lineárních rovnic substituční metodou („školní metoda“).
– Řešení soustavy sčítáním (odečítáním) soustav soustavy po členech.
–Řešení systému pomocí Cramerových vzorců.
–Řešení soustavy pomocí inverzní matice.
–Řešení soustavy Gaussovou metodou.
KRAMER
Nejprve zvažte Cramerovo pravidlo pro systém dvou lineárních rovnic se dvěma neznámými. Existují soustavy lineárních rovnic se dvěma proměnnými, které je vhodné řešit přesně podle Cramerova pravidla!
Uvažujme soustavu rovnic 
V prvním kroku vypočítáme determinant , je tzv hlavní determinant systému.
Jestliže , pak systém má nekonečně mnoho řešení nebo je nekonzistentní (nemá žádná řešení). V tomto případě Cramerovo pravidlo nepomůže, musíte použít Gaussova metoda.
Jestliže , pak má systém jedinečné řešení a abychom našli kořeny, musíme vypočítat další dva determinanty: a
V praxi mohou být výše uvedené kvalifikátory také označeny latinkou.
Kořeny rovnice najdeme podle vzorců:,
Příklad 7
Řešte soustavu lineárních rovnic
Vidíme, že koeficienty rovnice jsou poměrně velké, na pravé straně jsou desetinné zlomky s čárkou. Čárka je v praktických úlohách z matematiky poměrně vzácným hostem, tento systém jsem převzal z ekonometrického problému.
Jak takový systém vyřešit? Můžete se pokusit vyjádřit jednu proměnnou pomocí druhé, ale v tomto případě se vám jistě dostanou příšerné efektní zlomky, se kterými je extrémně nepohodlné pracovat a návrh řešení bude vypadat prostě příšerně. Druhou rovnici můžete násobit 6 a odečítat člen po členu, ale zde se objeví stejné zlomky.
Co dělat? V takových případech přijdou na pomoc Cramerovy vzorce.
Systém má tedy unikátní řešení.
;
; 
Jak vidíte, kořeny se ukázaly jako iracionální a byly nalezeny přibližně, což je pro ekonometrické problémy docela přijatelné (a dokonce běžné).
Komentáře zde nejsou potřeba, protože úloha je řešena podle hotových vzorců, je tu však jedno upozornění. Při použití této metody povinný Fragmentem zadání je následující fragment: « , takže systém má unikátní řešení . V opačném případě vás může recenzent potrestat za nerespektování Cramerovy věty.
Nebude zbytečné kontrolovat, což je vhodné provést na kalkulačce: nahradíme přibližné hodnoty na levé straně každé rovnice systému. Výsledkem je, že s malou chybou by měla být získána čísla, která jsou na pravé straně.
Cramerovy vzorce
Cramerova metoda spočívá v tom, že postupně nacházíme identifikátor hlavního systému(5.3), tzn. matice A determinant
A n pomocné determinanty D i (i= ), které se získají z determinantu D nahrazením i-tého sloupce sloupcem volných členů.
Cramerovy vzorce mají tvar:
D x x i = D i (i =). (5.4)
Z (5.4) vyplývá Cramerovo pravidlo, které dává vyčerpávající odpověď na otázku kompatibility systému (5.3): je-li hlavní determinant systému nenulový, pak má systém jednoznačné řešení, určené vzorcem:
Jestliže hlavní determinant soustavy D a všechny pomocné determinanty D i = 0 (i= ), pak má soustava nekonečný počet řešení. Pokud je hlavní determinant systému D = 0 a alespoň jeden pomocný determinant je odlišný od nuly, pak je systém nekonzistentní.
Příklad 1.14. Vyřešte soustavu rovnic Cramerovou metodou:
x 1 + x 2 + x 3 + x 4 = 5, x 1 + 2x 2 - x 3 + 4x 4 = -2, 2x 1 - 3x 2 - x 3 - 5x 4 = -2, 3x 1 + x 2 + 2x3 + 11x4 = 0.
Řešení. Hlavním determinantem tohoto systému D = 
= -142 ¹ 0, takže systém má jedinečné řešení. Vypočtěte pomocné determinanty D i (i= ) získané z determinantu D tak, že v něm nahradíme sloupec složený z koeficientů v x i sloupcem volných členů: D 1 = 
= -142, D2= 
= -284, D3= 
= - 426,
D4= 
= 142. Proto x 1 = D 1 / D = 1, x 2 = D 2 / D = 2, x 3 = D 3 / D = 3, x 4 = D 4 / D = -1, řešení soustavy je vektor C = (1, 2, 3, -1) T.
Základní pojmy soustav lineárních rovnic. Gaussova metoda.
VIZ VÝŠE.
Gauss-Jordanova metoda(metoda úplné eliminace neznámých) - metoda, která se používá k řešení čtvercových soustav lineárních algebraických rovnic, nalezení inverze matice, zjištění souřadnic vektoru v dané bázi nebo zjištění hodnosti matice. Metoda je modifikací Gaussovy metody.
Algoritmus
1. Vyberte první levý sloupec matice, který má alespoň jednu nenulovou hodnotu.
2. Pokud je nejvyšší číslo v tomto sloupci nula, vyměňte celý první řádek matice za jiný řádek matice, kde v tomto sloupci není žádná nula.
3. Všechny prvky prvního řádku jsou rozděleny horním prvkem vybraného sloupce.
4. Od zbývajících řádků odečtěte první řádek, vynásobený prvním prvkem odpovídajícího řádku, abyste dostali první prvek každého řádku (kromě prvního) nulu.
6. Po zopakování tohoto postupu jednou se získá horní trojúhelníková matice
7. Od předposlední řady odečtěte poslední řadu vynásobenou příslušným koeficientem tak, aby v předposlední řadě zůstala pouze 1 na hlavní diagonále.
8. Opakujte předchozí krok pro další řádky. V důsledku toho se získá identitní matice a řešení na místě volného vektoru (je nutné s ním provádět všechny stejné transformace).
9. Chcete-li získat inverzní matici, musíte na matici identity aplikovat všechny operace ve stejném pořadí.
Gaussova metoda
Historicky první, nejrozšířenější metodou řešení soustav lineárních rovnic je Gaussova metoda neboli metoda postupného odstraňování neznámých. Podstata této metody spočívá v tom, že pomocí postupných eliminací neznámých se daný systém přemění na stupňovitý (zejména trojúhelníkový) systém ekvivalentní danému. Při praktickém řešení soustavy lineárních rovnic Gaussovou metodou je vhodnější redukovat do stupňovitého tvaru nikoli soustavu rovnic samotnou, ale rozšířenou matici této soustavy, na jejích řádcích provádět elementární transformace. Matice postupně získané při transformaci jsou obvykle spojeny znakem ekvivalence.
Příklad 1.13. Soustavu rovnic řešte Gaussovou metodou: x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0.
Řešení. Píšeme rozšířenou matici tohoto systému
a na jeho řádcích proveďte následující elementární transformace: a) od jeho druhého a třetího řádku odečtěte první, vynásobený 3 a 2, v tomto pořadí: ~ 
;
b) vynásobte třetí řádek číslem (-5) a přidejte k němu druhý: 
.
V důsledku všech těchto transformací je tento systém redukován do trojúhelníkového tvaru: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.
Z poslední rovnice zjistíme z = -1,3. Dosazením této hodnoty do druhé rovnice máme y = -1,2. Dále z první rovnice dostáváme x = - 0,7
Z NOTEBOOKU:
Gaussova metoda
Metoda se skládá ze dvou částí – vpřed a vzad.
Přímý pohyb spočívá v chování expanze matice SLE do stupňovitého tvaru pomocí elementárních řádkových transformací. Ve stupňovité matici má každý následující řádek na začátku více nul než předchozí – nebo je nulový
Příklad:
Základní transformace řádků matice je:
1) přičtení čísel jednoho řádku matice, vynásobených nějakým číslem, do jednoho z nižších řádků matice.
2) Změňte dva řádky na místech
Zpětný pohyb Gaussovy metody spočívá v sekvenčním vyjádření některých proměnných z hlediska jiných, počínaje spodní nulou. Výsledkem je obecné řešení.
Po dopředném tahu existují 3 možnosti pro stupňovitý typ rozšířené matice:
1) Každý další řádek má na začátku přesně o jednu nulu více než ten předchozí
Příklad:
Rovnici napíšeme řádek po řádku a začneme zjišťovat hodnotu proměnných od spodního řádku.
4X 4 \u003d 8Þ X 4 \u003d 2
Dosaďte v předchozí rovnici
2X 3 -3X 4 \u003d -8 tj. 2X 3 -3 * 2 \u003d -8 nebo 2X 3 \u003d -2, Þ X 3 \u003d -1, nahraďte X3 a X4 ve druhém řádku atd. Získáme jediné řešení SLU
2) Počet nenulových řádků je menší než počet proměnných. Pak jeden z řádků obsahuje na začátku nuly alespoň o 2 více než předchozí a uvažujeme, že následující nenulový řádek nemá tvar (0 ... 0 b), kde číslo b=0
Například:
3) Poslední nenulový řádek má tvar (0…0/b), kde b=0 odpovídá protichůdným rovnostem o=b, systém je tedy nekompatibilní
Řešení SLE Gaussovou metodou
2X 1 + 3X 2 + X 3 \u003d 1
4X 1 + 5X 2 + 4X 3 = 7
6X 1 +10X 2 -3X 3 = -10
Složíme rozšířenou matici přímého pohybu.
Výpočet determinantů n- pořadí:Pojem determinantu n-tý řád
Pomocí tohoto článku o determinantech se určitě naučíte, jak řešit problémy, jako jsou následující:
Řešte rovnici:
a mnoho dalších, které učitelé tak rádi vymýšlejí.
Maticový determinant nebo jednoduše determinant hraje důležitou roli při řešení soustav lineárních rovnic. Obecně byly pro tento účel vynalezeny determinanty. Protože se často říká také "determinant matice", zmíníme se zde i o maticích. Matrix je obdélníková tabulka složená z čísel, která nelze zaměnit. Čtvercová matice je tabulka, která má stejný počet řádků a sloupců. Pouze čtvercová matice může mít determinant.
Logiku zápisu determinantů lze snadno pochopit podle následujícího schématu. Vezměme si soustavu dvou rovnic se dvěma neznámými, které znáte ze školy:
V determinantu jsou koeficienty pro neznámé postupně zapsány: v prvním řádku - z první rovnice, ve druhém řádku - z druhé rovnice:
Pokud je například uvedena soustava rovnic
pak se z koeficientů neznámých vytvoří následující determinant:
Řekněme tedy, že máme čtvercovou tabulku sestávající z čísel uspořádaných v nřádky (horizontální řady) a v n sloupce (svislé řádky). Pomocí těchto čísel podle některých pravidel, která prostudujeme níže, najdou číslo, na které zavolají determinant nřádu a jsou označeny takto:
(1)
Volají se čísla Prvky determinant (1) (první index znamená číslo řádku, druhý - číslo sloupce, na jehož průsečíku je prvek; i = 1, 2, ..., n; j= 1, 2, ..., n). Pořadí determinantu je počet jeho řádků a sloupců.
Pomyslná přímka spojující prvky determinantu, pro kterou jsou oba indexy stejné, tzn. Prvky
volala hlavní úhlopříčka, druhá úhlopříčka je boční.
Výpočet determinantů druhého a třetího řádu
Ukažme si, jak se počítají determinanty prvních tří řádů.
Určujícím prvkem prvního řádu je samotný prvek, tj.
Druhým determinantem řádu je číslo získané takto:
, (2)
Součin prvků na hlavní a vedlejší diagonále.
Rovnost (2) ukazuje, že součin prvků hlavní úhlopříčky se bere s jejím znaménkem a součin prvků vedlejší úhlopříčky se bere s opačným znaménkem. .
Příklad 1 Vypočítejte determinanty druhého řádu:
Řešení. Podle vzorce (2) zjistíme:
Determinant třetího řádu je číslo získané takto:
(3)
Je těžké si tento vzorec zapamatovat. Existuje však jednoduché pravidlo tzv trojúhelníkové pravidlo , což usnadňuje reprodukci výrazu (3). Prvky determinantu označíme body, spojíme úsečkami ty z nich, které dávají součiny prvků determinantu (obr. 1).
Vzorec (3) ukazuje, že součiny prvků hlavní úhlopříčky, jakož i prvky umístěné ve vrcholech dvou trojúhelníků, jejichž základny jsou s ní rovnoběžné, jsou brány se svými znaménky; s opačnými - produkty prvků sekundární úhlopříčky, stejně jako prvky umístěné ve vrcholech dvou trojúhelníků, které jsou s ní rovnoběžné .
Na obr.1 jsou červeně zvýrazněny hlavní úhlopříčka a základny jí odpovídajících trojúhelníků a vedlejší úhlopříčka a základny jí odpovídajících trojúhelníků.
Při výpočtu determinantů je velmi důležité, stejně jako na střední škole, pamatovat na to, že mínusové číslo vynásobené mínusovým číslem dává znaménko plus a plus násobené mínusovým číslem dává číslo se znaménkem mínus.
Příklad 2 Vypočítejte determinant třetího řádu:
Řešení. Pomocí pravidla trojúhelníků dostaneme
Výpočet determinantů n-tý řád
Řádková nebo sloupcová expanze determinantu
K výpočtu determinantu nřádu, je nutné znát a používat následující větu.
Laplaceova věta. Determinant je roven součtu součinů prvků libovolné řady a jejich algebraických doplňků, tzn.
Definice. Pokud v determinantu n pořadí zvolit libovolně p linky a p sloupce ( p < n), pak prvky v průsečíku těchto řádků a sloupců tvoří matici pořadí.
Determinant této matice se nazývá Méně důležitý původní determinant. Zvažte například determinant:
Sestavme matici z řádků a sloupců se sudými čísly:
Determinant
volala Méně důležitý determinant . Přijat nezletilý druhého řádu. Je jasné, že lze zkonstruovat různé nezletilé prvního, druhého a třetího řádu.
Vezmeme-li prvek a přeškrtneme řádek a sloupec, na jehož průsečíku v determinantu stojí, dostaneme moll, nazývaný moll prvku, který označíme:
.
Pokud se vedlejší vynásobí , kde 3 + 2 je součet čísel řádků a sloupců, na jejichž průsečíku prvek stojí, pak se výsledný součin nazývá algebraické sčítání prvek a je označen ,
Obecně se moll prvku označí a algebraický doplněk bude ,
(4)
Vypočítejme například algebraické doplňky prvků a determinant třetího řádu:
Podle vzorce (4) dostaneme 
Při rozkladu determinantu se často používá následující vlastnost determinantu n- pořadí:
pokud je součin odpovídajících prvků jiného řádku nebo sloupce konstantním faktorem přidán k prvkům libovolného řádku nebo sloupce, pak se hodnota determinantu nezmění.
Příklad 4
Předběžně odečteme prvky čtvrté řady od prvního a třetího řádku, pak budeme mít
Ve čtvrtém sloupci získaného determinantu jsou tři prvky nuly. Proto je výhodnější rozšířit tento determinant o prvky čtvrtého sloupce, protože první tři produkty budou nulové. Proto
Řešení můžete zkontrolovat pomocí online kalkulačka determinantů .
A následující příklad ukazuje, jak lze výpočet determinantu libovolného (v tomto případě čtvrtého) řádu zredukovat na výpočet determinantu druhého řádu.
Příklad 5 Vypočítejte determinant:
Odečteme prvky prvního řádku od třetího řádku a přidáme prvky prvního řádku k prvkům čtvrtého řádku, pak budeme mít
V prvním sloupci jsou všechny prvky kromě prvního nulové. To znamená, že determinant lze rozložit již v prvním sloupci. Ale opravdu nechceme počítat determinant třetího řádu. Provedeme proto více transformací: k prvkům třetí řady přidáme prvky druhé řady vynásobené 2 a prvky druhé řady odečteme od prvků čtvrté řady. Výsledkem je, že determinant, který je algebraickým doplňkem, může být rozšířen v prvním sloupci a budeme muset vypočítat pouze determinant druhého řádu a nenechat se zmást ve znaménkách:
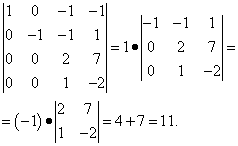
Uvedení determinantu do trojúhelníkového tvaru
Determinant, kde jsou všechny prvky ležící na jedné straně jedné z úhlopříček rovny nule, se nazývá trojúhelníkový. Případ vedlejší úhlopříčky se redukuje na případ hlavní úhlopříčky obrácením pořadí řádků nebo sloupců. Takový determinant je roven součinu prvků hlavní diagonály.
Pro redukci na trojúhelníkový tvar se používá stejná vlastnost determinantu nřádu, který jsme použili v předchozím odstavci: přičteme-li součin odpovídajících prvků jiného řádku nebo sloupce konstantním faktorem k prvkům libovolného řádku nebo sloupce, pak se hodnota determinantu nezmění.
Řešení můžete zkontrolovat pomocí online kalkulačka determinantů .
Determinantní vlastnosti n-tý řád
Ve dvou předchozích odstavcích jsme již použili jednu z vlastností determinantu n-tý řád. V některých případech můžete pro zjednodušení výpočtu determinantu použít další důležité vlastnosti determinantu. Například je možné redukovat determinant na součet dvou determinantů, z nichž jeden nebo oba lze pohodlně rozšířit podél nějakého řádku nebo sloupce. Existuje mnoho případů takového zjednodušení a otázka použití té či oné vlastnosti determinantu by se měla řešit individuálně.
Maticový determinant (maticový determinant) je čtvercová tabulka čísel nebo matematických symbolů ( Δd).
Definice. maticový determinant n×n je číslo:
kde ( α 1, α 2,...,α n) - permutace čísel od 1 před n, N (α 1 ,α 2 ,...,α n)- počet inverzí v permutaci, k součtu dochází přes všechny možné permutace řádu n.
Maticový determinant A v podstatě označované jako de t(A), |A|, nebo ?(A).
Parametry, s jejichž pomocí se nalézá řešení všech typů algebraických matic.
Na najít maticový determinant je nutné znát základní vlastnosti matic a posloupnost akcí při řešení matice.
- Pro řádové matice n=2 determinant se najde pomocí vzorce: Δ= a11*22-12*21
- Pro řádové matice n=3 determinant se nalézá pomocí algebraických sčítání nebo pomocí Sarrusovy metody.
- Matice s rozměrem >3 je rozložena na algebraické sčítání, pro které jsou nalezeny jejich determinanty (minor). Například determinant matice 4. řádu se vypočítá pomocí rozšíření v řádcích nebo sloupcích.
Pro nalézací maticový determinant, který obsahuje funkce v matici, se používají standardní metody. Chcete-li například najít determinant matice třetího řádu:
Použijme rozšíření na prvním řádku:
Δ = sin(x) × + 1× = 2sin(x) cos(x) - 2cos(x) = sin(2x) - 2cos(x)
Vypočítejte determinant matice.
Vypočítejte determinant matice Existuje několik metod, které jsou uvedeny níže.
Nejoblíbenějším způsobem výpočtu determinantu matice je metoda výběru algebraických sčítání. Existuje jednodušší verze této metody – výpočet determinantu pomocí Sarrusova pravidla. Tyto metody se liší při výpočtu determinantu jednoduché malé matice a pokud potřebujete vypočítat matici velkých rozměrů, pak např. metody výpočtu determinant matice:
- výpočet determinantu metodou redukce objednávky,
- výpočet determinantu Gaussovou metodou (redukcí matice na trojúhelníkový tvar),
- výpočet determinantu dekompoziční metodou.
V Excelu se pro výpočet determinantu používá funkce = MOPRED (rozsah buněk).