ΚΑΘΟΡΙΣΤΙΚΟΣ
ή ορίζουσα, - στα μαθηματικά, η εγγραφή αριθμών με τη μορφή τετράγωνου πίνακα, σύμφωνα με τον οποίο τίθεται ένας άλλος αριθμός (η «τιμή» της ορίζουσας). Πολύ συχνά, ο όρος «ορίζουσα» σημαίνει τόσο την έννοια της ορίζουσας όσο και τη μορφή της σημειογραφίας της. Οι ορίζοντες καθιστούν δυνατή την εύκολη εγγραφή σύνθετων εκφράσεων που προκύπτουν, για παράδειγμα, κατά την επίλυση γραμμικών εξισώσεων στην αναλυτική γεωμετρία και στη μαθηματική ανάλυση. Η ανακάλυψη των προσδιοριστικών αποδίδεται στον Ιάπωνα μαθηματικό S. Kova (1683) και, ανεξάρτητα, στον G. Leibniz (1693). Η σύγχρονη θεωρία ανάγεται στα έργα των J. Binet, O. Cauchy και C. Jacobi στις αρχές του 19ου αιώνα. Η απλούστερη ορίζουσα αποτελείται από 4 αριθμούς, που ονομάζονται στοιχεία, διατεταγμένοι σε 2 σειρές και 2 στήλες. Μια τέτοια ορίζουσα λέγεται ότι είναι 2ης τάξης. Για παράδειγμα, αυτός είναι ο καθοριστικός παράγοντας
Η τιμή των οποίων είναι 2*5 - 3*1 (δηλαδή 10 - 3 ή 7). Στη γενική περίπτωση, η ορίζουσα 2ης τάξης συνήθως γράφεται στη μορφή
Και η τιμή του είναι a1b2 - a2b1, όπου τα a και b είναι αριθμοί ή συναρτήσεις. Η ορίζουσα 3ης τάξης αποτελείται από 9 στοιχεία διατεταγμένα σε 3 σειρές και 3 στήλες. Γενικά, η ορίζουσα νης τάξης αποτελείται από n2 στοιχεία και συνήθως γράφεται ως
Ο πρώτος δείκτης κάθε στοιχείου υποδεικνύει τον αριθμό της σειράς, ο δεύτερος - τον αριθμό της στήλης στη διασταύρωση της οποίας βρίσκεται αυτό το στοιχείο, επομένως το aij είναι το στοιχείο της i-ης σειράς και της j-ης στήλης. Συχνά μια τέτοια ορίζουσα γράφεται ως |aij|. Μία από τις μεθόδους για τον υπολογισμό της ορίζουσας, που χρησιμοποιείται σχεδόν πάντα στον υπολογισμό οριζόντων υψηλότερης τάξης, είναι η επέκταση σε "ελάσσονες". Ένα δευτερεύον στοιχείο που αντιστοιχεί σε οποιοδήποτε στοιχείο της ορίζουσας είναι μια ορίζουσα τάξης μικρότερης του 1, που λαμβάνεται από την αρχική διαγράφοντας τη γραμμή και τη στήλη στη διασταύρωση των οποίων βρίσκεται αυτό το στοιχείο. Για παράδειγμα, το δευτερεύον που αντιστοιχεί στο στοιχείο a2 από την ορίζουσα
Το "αλγεβρικό συμπλήρωμα" ενός στοιχείου είναι το δευτερεύον του, που λαμβάνεται με πρόσημο συν εάν το άθροισμα των αριθμών της γραμμής και της στήλης στη τομή των οποίων βρίσκεται το στοιχείο είναι άρτιο, και με πρόσημο μείον εάν είναι περιττό. Στο παραπάνω παράδειγμα, το στοιχείο a2 βρίσκεται στην 1η στήλη και στη 2η σειρά. το άθροισμα (1 + 2) είναι περιττό, και επομένως το αλγεβρικό συμπλήρωμα του στοιχείου a2 ισούται με το ελάσσονα του, λαμβανόμενο με πρόσημο μείον, δηλ.
Η τιμή της ορίζουσας ισούται με το άθροισμα των γινομένων των στοιχείων οποιασδήποτε γραμμής (ή οποιασδήποτε στήλης) και των αλγεβρικών συμπληρωμάτων τους. Για παράδειγμα, η ορίζουσα
επεκτείνεται πάνω από την πρώτη στήλη έχει τη μορφή
και η επέκτασή του στη δεύτερη σειρά έχει τη μορφή
Υπολογίζοντας κάθε δευτερεύον και πολλαπλασιάζοντάς το με έναν συντελεστή, είναι εύκολο να επαληθεύσουμε ότι και οι δύο παραστάσεις είναι ίδιες. Η τιμή της ορίζουσας. Κάτω από την τιμή της ορίζουσας
Είναι σύνηθες να κατανοούμε το άθροισμα όλων των γινομένων των n στοιχείων, δηλ.
Σε αυτόν τον τύπο, η άθροιση πραγματοποιείται σε όλες τις μεταθέσεις j1, j, jn των αριθμών 1, 2, j, n και προηγείται του όρου ένα σύμβολο συν εάν η μετάθεση είναι άρτια και ένα σύμβολο μείον εάν αυτή η μετάθεση είναι περιττή . Ένα τέτοιο άθροισμα είναι ακριβώς n! μέλη, τα μισά από τα οποία λαμβάνονται με σύμβολο συν, τα μισά - με σύμβολο μείον. Κάθε όρος αθροίσματος περιέχει έναν όρο από κάθε στήλη και κάθε γραμμή της ορίζουσας. Μπορεί να αποδειχθεί ότι αυτό το άθροισμα συμπίπτει με την έκφραση που προκύπτει με την επέκταση της ορίζουσας σε ανηλίκους.
Καθοριστικές ιδιότητες.Μεταξύ των σημαντικότερων ιδιοτήτων της ορίζουσας αναφέρουμε τα ακόλουθα. (i) Εάν όλα τα στοιχεία οποιασδήποτε γραμμής (ή οποιασδήποτε στήλης) είναι μηδέν, τότε η τιμή της ορίζουσας είναι επίσης μηδέν:
(ii) Εάν τα στοιχεία δύο σειρών (ή δύο στηλών) είναι ίσα ή ανάλογα, τότε η τιμή της ορίζουσας είναι μηδέν:
(iii) Η τιμή της ορίζουσας δεν αλλάζει εάν εναλλάσσονται όλες οι σειρές και οι στήλες της, δηλ. γράψτε την πρώτη γραμμή ως πρώτη στήλη, τη δεύτερη γραμμή ως δεύτερη στήλη, και ούτω καθεξής. (αυτή η λειτουργία ονομάζεται μεταφορά). Για παράδειγμα,
(iv) Η τιμή της ορίζουσας δεν αλλάζει αν προσθέσουμε στα στοιχεία μιας σειράς (ή στήλης) τα αντίστοιχα στοιχεία μιας άλλης γραμμής (ή στήλης) πολλαπλασιαζόμενα με έναν αυθαίρετο παράγοντα. Το παρακάτω παράδειγμα πολλαπλασιάζει τα στοιχεία της δεύτερης σειράς με -2 και τα προσθέτει στα στοιχεία της πρώτης σειράς:
(v) Εάν ανταλλάσσονται δύο σειρές (ή δύο στήλες), η ορίζουσα αλλάζει πρόσημο:
(vi) Εάν όλα τα στοιχεία μιας γραμμής (ή μιας στήλης) περιέχουν έναν κοινό παράγοντα, τότε αυτός ο παράγοντας μπορεί να αφαιρεθεί από το πρόσημο της ορίζουσας:
Παράδειγμα. Υπολογίστε την τιμή της ακόλουθης ορίζουσας 4ης τάξης:
Ας προσθέσουμε την 4η γραμμή στην 1η γραμμή:
Αφαιρέστε την 1η στήλη από την 4η στήλη:
Πολλαπλασιάστε την 3η στήλη με 3 και αφαιρέστε από την 4η στήλη:
Μπορείτε να ανταλλάξετε γραμμές και στήλες εάν θέλετε:
Ας επεκτείνουμε την ορίζουσα με τα στοιχεία της τέταρτης σειράς. Τρία στοιχεία αυτής της σειράς είναι ίσα με μηδέν, το μη μηδενικό στοιχείο βρίσκεται στην τρίτη στήλη και επειδή το άθροισμα (3 + 4) είναι περιττό, το αλγεβρικό συμπλήρωμά του έχει πρόσημο μείον. Ως αποτέλεσμα, παίρνουμε:
Το δευτερεύον μπορεί να αποσυντεθεί σε στοιχεία της τρίτης σειράς: δύο από τα στοιχεία του είναι ίσα με μηδέν και ένα μη μηδενικό στοιχείο βρίσκεται στην τρίτη στήλη. το άθροισμα (3 + 3) είναι άρτιο, οπότε η προηγούμενη ισότητα μπορεί να συνεχιστεί:
Εφαρμογές. Επίλυση συστήματος εξισώσεων
μπορεί να ληφθεί πολλαπλασιάζοντας την πρώτη εξίσωση με b2, τη δεύτερη με b1 και στη συνέχεια αφαιρώντας τη μία εξίσωση από την άλλη. Κάνοντας αυτές τις λειτουργίες, παίρνουμε
Ή εάν
έπειτα
Μια τέτοια καταγραφή της λύσης με τη βοήθεια οριζόντων επιτρέπει τη γενίκευση στην περίπτωση επίλυσης ενός συστήματος n γραμμικών εξισώσεων με n αγνώστους. κάθε ορίζουσα θα είναι της νης τάξης. Ορίζουσα συστήματος γραμμικών εξισώσεων
θα
Σημειώστε ότι εάν D = 0, τότε οι εξισώσεις είναι είτε ασυνεπείς είτε όχι ανεξάρτητες. Επομένως, ο προκαταρκτικός υπολογισμός της ορίζουσας D σάς επιτρέπει να ελέγξετε εάν το σύστημα γραμμικών εξισώσεων είναι επιλύσιμο.
Ορίζοντες στην αναλυτική γεωμετρία.Η γενική εξίσωση μιας κωνικής τομής μπορεί να αναπαρασταθεί ως
Καθοριστικός
λέγεται ο διαχωριστής. Εάν D = 0, τότε η καμπύλη εκφυλίζεται σε ένα ζεύγος παράλληλων ή τεμνόμενων γραμμών ή σε ένα σημείο (βλ. επίσης ΚΩΝΙΚΕΣ ΕΝΟΤΗΤΕΣ). Ένα άλλο παράδειγμα: το εμβαδόν του τριγώνου Α με κορυφές σε σημεία (παράκαμψη - αριστερόστροφα) (x1, y1), (x2, y2) και (x3, y3) δίνεται από
Σύνδεση οριζόντων με πίνακες.Ένας πίνακας είναι μια εγγραφή ενός πίνακα αριθμών με τη μορφή ενός ορθογώνιου πίνακα. Οι ορίζοντες σχετίζονται με τετράγωνους πίνακες. για παράδειγμα, ορίζουσα μήτρας
Αν τα Α, Β και С είναι τετράγωνοι πίνακες και τότε |A|*|B| = |C|.
δείτε επίσηςΗ ΑΛΓΕΒΡΑ ΕΙΝΑΙ ΠΕΡΙΛΗΨΗ.
Jacobian.Αν x = f (u, v), y = g (u, v) είναι μετασχηματισμός συντεταγμένων, τότε η ορίζουσα
Ονομάζεται Jacobian ή Jacobi ορίζουσα αυτού του μετασχηματισμού. Αν το J δεν είναι ίσο με 0 σε κάποιο σημείο, τότε στη γειτονιά του οι εξισώσεις μετασχηματισμού μπορούν να λυθούν μοναδικά ως προς το u και το v, παριστάνοντάς τα ως συναρτήσεις των x και y.
Δείτε ΜΑΘΗΜΑΤΙΚΗ ΑΝΑΛΥΣΗ.
Εγκυκλοπαίδεια Collier. - Ανοιχτή κοινωνία. 2000 .
Συνώνυμα:Δείτε τι είναι το "DETERMINANT" σε άλλα λεξικά:
ΚΑΘΟΡΙΣΤΙΚΟΣ, καθοριστικός, αρσενικός. (Βιβλίο). 1. Αυτό που καθορίζει, εκφράζει κάτι. 2. Βιβλίο που χρησιμεύει ως αναφορά στον προσδιορισμό κάτι (επιστημονικού). Αναγνώριση φυτών. Οδηγός μανιταριών. 3. Μια έκφραση που αποτελείται από ... ... Επεξηγηματικό Λεξικό Ushakov
- (ορίζουσα) μια μαθηματική έκφραση που συντάσσεται σύμφωνα με έναν ορισμένο κανόνα από n2 αριθμούς, που χρησιμοποιείται στην επίλυση και τη μελέτη συστημάτων αλγεβρικών εξισώσεων 1ου βαθμού. Ο αριθμός n ονομάζεται σειρά της ορίζουσας. Έτσι, η ορίζουσα της 2ης τάξης ... Μεγάλο Εγκυκλοπαιδικό Λεξικό
Αναγνωριστικό, Hessian, δευτερεύον, προσδιοριστικό Λεξικό ρωσικών συνωνύμων. προσδιοριστικό ουσιαστικού, αριθμός συνωνύμων: 10 αυτοπροσδιοριστής (1) … Συνώνυμο λεξικό
ΚΑΘΟΡΙΣΤΙΚΟΣ- (ορίζουσα) μια μαθηματική έκφραση που συντάσσεται σύμφωνα με έναν ορισμένο κανόνα από n2 αριθμούς, που χρησιμοποιείται στην επίλυση και τη μελέτη συστημάτων αλγεβρικών εξισώσεων 1ου βαθμού. Ο αριθμός n ονομάζεται σειρά της ορίζουσας. Έτσι, η ορίζουσα της 2ης τάξης ... Μεγάλη Πολυτεχνική Εγκυκλοπαίδεια
ΟΡΙΣΤΙΚΟΣ, εγώ, σύζυγος. 1. Μια συσκευή για τον προσδιορισμό του n., καθώς και γενικά, με τη βοήθεια του οποίου είναι δυνατό να n. καθορίσει ακριβώς. Τηλέφωνο με αναγνώριση κλήσης. Ο. ρυθμός. 2. Ένα βιβλίο για αναφορά κατά τον προσδιορισμό του τι ν. (ειδικός.). Ο. φυτά ... Επεξηγηματικό λεξικό Ozhegov
- (ορίζουσα) του τετραγωνικού πίνακα A = ||aij|| σειρά n, detA πολυώνυμο… Φυσική Εγκυκλοπαίδεια
καθοριστικός- - Θέματα τηλεπικοινωνιών, βασικές έννοιες EN καθοριστικό ... Εγχειρίδιο Τεχνικού Μεταφραστή
Αυτός ο όρος έχει άλλες έννοιες, βλέπε Καθοριστικός (έννοιες). Η ορίζουσα (ή ορίζουσα) είναι μια από τις βασικές έννοιες της γραμμικής άλγεβρας. Η ορίζουσα μήτρας είναι ένα πολυώνυμο στα στοιχεία ενός τετραγωνικού πίνακα (δηλαδή, έτσι ώστε y ... Wikipedia
καθοριστικός- Προκριματικός 3.4.6 (βοηθητικός): Κωδικός βοηθητικής κλάσης UDC. Μια πηγή … Λεξικό-βιβλίο αναφοράς όρων κανονιστικής και τεχνικής τεκμηρίωσης
ΕΓΩ; μ. 1. Βιβλίο. Αυτό που καθορίζεται, καθορίζεται από αυτό που λ. Ο ήχος μπορεί να είναι καθοριστικός παράγοντας της ταχύτητας. Ο κύριος καθοριστικός παράγοντας του χρόνου είναι η κίνηση του Ήλιου στο διάστημα. 2. Spec. Ένας οδηγός (βιβλίο ή πίνακας) για να προσδιορίσετε τι ... ... εγκυκλοπαιδικό λεξικό
Βιβλία
- Κλειδί για τα αγγειόσπερμα των ξυλωδών φυτών από φρούτα και σπόρους, Sinitsyn Evgeny Mikhailovich. Η ορίζουσα αποτελείται από δύο μέρη. Το πρώτο μέρος είναι ένας πίνακας για την αναγνώριση γενών και το δεύτερο περιλαμβάνει πίνακες για την αναγνώριση ειδών αγγειόσπερμων ξυλωδών φυτών κατά ...
· καθοριστικός τετράγωνο πίνακες Α της νης τάξης ή ορίζουσα nης τάξης ονομάζεται αριθμός ίσος με το αλγεβρικό άθροισμα Π! μέλη, καθένα από τα οποία είναι ένα προϊόν Πστοιχεία μήτρας που λαμβάνονται ένα από κάθε σειρά και κάθε στήλη με συγκεκριμένα σημάδια. Η ορίζουσα συμβολίζεται με ή .
Ορίζουσα δεύτερης τάξηςείναι ένας αριθμός που εκφράζεται ως εξής: 
. Για παράδειγμα 
.
Ορίζουσα τρίτης τάξηςυπολογίζεται σύμφωνα με τον κανόνα των τριγώνων (κανόνας Sarrus): .
Παράδειγμα. .
Σχόλιο. Στην πράξη, οι ορίζοντες τρίτης τάξης, καθώς και οι υψηλότερες τάξεις, υπολογίζονται χρησιμοποιώντας τις ιδιότητες των οριζόντων.
Ιδιότητες προσδιοριστικών nης τάξης.
1. Η τιμή της ορίζουσας δεν θα αλλάξει εάν κάθε σειρά (στήλη) αντικατασταθεί από μια στήλη (γραμμή) με τον ίδιο αριθμό - μεταθέτω.
2. Αν μία από τις σειρές (στήλη) της ορίζουσας αποτελείται από μηδενικά, τότε η τιμή της ορίζουσας είναι μηδέν.
3. Εάν δύο σειρές (στήλες) εναλλάσσονται στην ορίζουσα, τότε η απόλυτη τιμή της ορίζουσας δεν θα αλλάξει και το πρόσημο θα αλλάξει στο αντίθετο.
4. Η ορίζουσα που περιέχει δύο ίδιες σειρές (στήλες) ισούται με μηδέν.
5. Ο κοινός παράγοντας όλων των στοιχείων μιας σειράς (στήλης) μπορεί να αφαιρεθεί από το πρόσημο της ορίζουσας.
· Ανήλικος κάποιο στοιχείο της ορίζουσας Πη σειρά ονομάζεται ορίζουσα ( Π-1)-η σειρά, που λαμβάνεται από το πρωτότυπο διαγράφοντας τη γραμμή και τη στήλη στη διασταύρωση των οποίων βρίσκεται το επιλεγμένο στοιχείο. Ονομασία: .
· Αλγεβρική πρόσθεση Το στοιχείο της ορίζουσας ονομάζεται δευτερεύον του, λαμβάνεται με το πρόσημο . Ονομασία: Λοιπόν =.
6. Η ορίζουσα ενός τετραγωνικού πίνακα είναι ίση με το άθροισμα των γινομένων των στοιχείων οποιασδήποτε γραμμής (ή στήλης) και των αλγεβρικών συμπληρωμάτων τους ( θεώρημα αποσύνθεσης).
7. Αν κάθε στοιχείο της -ης σειράς είναι το άθροισμα κόρους, τότε η ορίζουσα αντιπροσωπεύεται ως άθροισμα κορίζουσες στις οποίες όλες οι σειρές, εκτός από τη -η σειρά, είναι ίδιες με την αρχική ορίζουσα και η -η σειρά στην πρώτη ορίζουσα αποτελείται από τους πρώτους όρους, στη δεύτερη - της δεύτερης κ.ο.κ. Το ίδιο ισχύει και για τις στήλες.
8. Η ορίζουσα δεν θα αλλάξει εάν σε μία από τις σειρές (στήλες) προστεθεί μια άλλη σειρά (στήλη) πολλαπλασιασμένη με έναν αριθμό.
Συνέπεια. Εάν στη σειρά (στήλη) της ορίζουσας προστεθεί ένας γραμμικός συνδυασμός των άλλων σειρών (στήλων) του, τότε η ορίζουσα δεν θα αλλάξει.
9. Η ορίζουσα ενός διαγώνιου πίνακα είναι ίση με το γινόμενο των στοιχείων στην κύρια διαγώνιο, δηλ.
Σχόλιο. Η ορίζουσα ενός τριγωνικού πίνακα είναι επίσης ίση με το γινόμενο των στοιχείων στην κύρια διαγώνιο.
Οι αναφερόμενες ιδιότητες των προσδιοριστικών παραγόντων καθιστούν δυνατή τη σημαντική απλοποίηση του υπολογισμού τους, κάτι που είναι ιδιαίτερα σημαντικό για καθοριστικούς παράγοντες υψηλής τάξης. Σε αυτήν την περίπτωση, συνιστάται ο μετασχηματισμός του αρχικού πίνακα με τέτοιο τρόπο ώστε ο μετασχηματισμένος πίνακας να έχει μια γραμμή ή στήλη που περιέχει όσο το δυνατόν περισσότερα μηδενικά («μηδενισμός» σειρών ή στηλών).
Παραδείγματα.Υπολογίστε ξανά την ορίζουσα που δόθηκε στο προηγούμενο παράδειγμα, χρησιμοποιώντας τις ιδιότητες των οριζόντων.
Λύση: Σημειώστε ότι στην πρώτη γραμμή υπάρχει ένας κοινός παράγοντας - 2, και στη δεύτερη - ένας κοινός παράγοντας 3, θα τους βγάλουμε από την ορίζουσα (από την ιδιότητα 5). Στη συνέχεια, επεκτείνουμε την ορίζουσα, για παράδειγμα, στην πρώτη στήλη, χρησιμοποιώντας την ιδιότητα 6 (θεώρημα επέκτασης).
Πιο αποτελεσματικο μέθοδος αναγωγής μιας ορίζουσας σε διαγώνια ή τριγωνική μορφή . Για τον υπολογισμό της ορίζουσας ενός πίνακα, αρκεί να πραγματοποιηθεί ένας μετασχηματισμός του πίνακα που δεν αλλάζει την ορίζουσα και καθιστά δυνατή τη μετατροπή του πίνακα σε διαγώνιο.
Συμπερασματικά, σημειώνουμε ότι αν η ορίζουσα ενός τετραγωνικού πίνακα είναι ίση με μηδέν, τότε ο πίνακας λέγεται εκφυλισμένος (ή ειδικό) , σε διαφορετική περίπτωση - μη εκφυλισμένος .
1. Η ορίζουσα δεν αλλάζει κατά τη μεταφορά.
2. Αν μία από τις σειρές της ορίζουσας αποτελείται από μηδενικά, τότε η ορίζουσα ισούται με μηδέν.
3. Εάν δύο σειρές αναδιαταχθούν στην ορίζουσα, η ορίζουσα θα αλλάξει πρόσημο.
4. Η ορίζουσα που περιέχει δύο όμοιες χορδές είναι ίση με μηδέν.
5. Αν όλα τα στοιχεία κάποιας σειράς της ορίζουσας πολλαπλασιαστούν με κάποιον αριθμό k, τότε η ίδια η ορίζουσα θα πολλαπλασιαστεί με k.
6. Η ορίζουσα που περιέχει δύο αναλογικές σειρές ισούται με μηδέν.
7. Αν όλα τα στοιχεία της i-ης σειράς της ορίζουσας παρουσιάζονται ως το άθροισμα δύο όρων aij = bj + cj (j= ), τότε η ορίζουσα ισούται με το άθροισμα των οριζουσών, στην οποία όλες οι σειρές, εκτός για την i-η σειρά, είναι ίδια με τη δεδομένη ορίζουσα , και η i-η σειρά σε ένα από τα αθροίσματα αποτελείται από στοιχεία bj , στην άλλη - από στοιχεία cj .
8. Η ορίζουσα δεν αλλάζει αν στα στοιχεία μιας σειράς της προστεθούν τα αντίστοιχα στοιχεία μιας άλλης σειράς πολλαπλασιασμένα με τον ίδιο αριθμό.
Σχόλιο.Όλες οι ιδιότητες παραμένουν έγκυρες εάν ληφθούν στήλες αντί για γραμμές.
ΑνήλικοςΤο M i j του στοιχείου a i j της ορίζουσας d της νης τάξης είναι η ορίζουσα της τάξης n-1, η οποία προκύπτει από το d διαγράφοντας τη σειρά και τη στήλη που περιέχουν αυτό το στοιχείο.
Αλγεβρική πρόσθεσηΤο στοιχείο a i j της ορίζουσας d είναι το ελάσσονα M i j , που λαμβάνεται με το πρόσημο (-1) i + j . Το αλγεβρικό συμπλήρωμα του στοιχείου a i j θα συμβολίζεται με A i j . Έτσι, A i j = (-1) i + j M i j .
Μέθοδοι για τον πρακτικό υπολογισμό οριζόντιων παραγόντων που βασίζονται στο γεγονός ότι η ορίζουσα της τάξης n μπορεί να εκφραστεί με όρους ορίζουσες κατώτερων τάξεων δίνονται από το ακόλουθο θεώρημα.
Θεώρημα (αποσύνθεση της ορίζουσας σε γραμμή ή στήλη).
Η ορίζουσα ισούται με το άθροισμα των γινομένων όλων των στοιχείων της αυθαίρετης γραμμής (ή στήλης) και των αλγεβρικών συμπληρωμάτων τους. Γίνεται δηλαδή αποσύνθεση του d ως προς τα στοιχεία της i-ης σειράς d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = )
ή j-η στήλη d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).
Συγκεκριμένα, εάν όλα τα στοιχεία μιας γραμμής (ή στήλης) εκτός από μία είναι ίσα με μηδέν, τότε η ορίζουσα είναι ίση με αυτό το στοιχείο πολλαπλασιαζόμενο με το αλγεβρικό συμπλήρωμά του.
Παράδειγμα 1.4.Μη υπολογισμός της ορίζουσας 
, να δείξετε ότι ισούται με μηδέν. Λύση.Αφαιρέστε την πρώτη σειρά από τη δεύτερη σειρά, παίρνουμε την ορίζουσα 
ίσο με το πρωτότυπο. Αν αφαιρέσουμε και την πρώτη σειρά από την τρίτη σειρά, παίρνουμε την ορίζουσα 
, στην οποία οι δύο σειρές είναι ανάλογες. Αυτή η ορίζουσα είναι μηδέν.
Παράδειγμα 1.5.Υπολογίστε την ορίζουσα D = 
, επεκτείνοντάς το κατά τα στοιχεία της δεύτερης στήλης.
Λύση.Ας επεκτείνουμε την ορίζουσα με τα στοιχεία της δεύτερης στήλης:
D = a 12 A 12 + a 22 A 22 + a 32 A 32 =
Παράδειγμα 1.6.Υπολογίστε την ορίζουσα
Α= 
, στην οποία όλα τα στοιχεία στη μία πλευρά της κύριας διαγωνίου είναι ίσα με μηδέν. Λύση.Ας επεκτείνουμε την ορίζουσα A στην πρώτη σειρά: A = a 11 A 11 = 
. Η ορίζουσα στα δεξιά μπορεί να επεκταθεί ξανά κατά μήκος της πρώτης γραμμής, τότε παίρνουμε:
Α= 
.Και τα λοιπά. Μετά από n βήματα, καταλήγουμε στην ισότητα A = a 11 a 22... a nn.
3.Βασικές έννοιες συστημάτων γραμμικών εξισώσεων. Θεώρημα Cramer.
Ορισμός. Σύστημα γραμμικών εξισώσεωνείναι η ένωση των nγραμμικές εξισώσεις, καθεμία από τις οποίες περιέχει κμεταβλητές. Είναι γραμμένο έτσι:
Πολλοί, όταν έρχονται αντιμέτωποι με υψηλότερη άλγεβρα για πρώτη φορά, πιστεύουν λανθασμένα ότι ο αριθμός των εξισώσεων πρέπει απαραίτητα να συμπίπτει με τον αριθμό των μεταβλητών. Στη σχολική άλγεβρα αυτό συμβαίνει συνήθως, αλλά για την ανώτερη άλγεβρα αυτό, γενικά, δεν ισχύει.
Ορισμός. Επίλυση συστήματος εξισώσεωνείναι μια ακολουθία αριθμών ( κ 1 ,κ 2 , ..., k n), που είναι λύση σε κάθε εξίσωση του συστήματος, δηλ. κατά την αντικατάσταση σε αυτή την εξίσωση αντί για μεταβλητές Χ 1 , Χ 2 , ..., x nδίνει τη σωστή αριθμητική τιμή.
Αντίστοιχα, λύσει το σύστημα των εξισώσεωνσημαίνει να βρεις το σύνολο όλων των λύσεών του ή να αποδείξεις ότι αυτό το σύνολο είναι κενό. Δεδομένου ότι ο αριθμός των εξισώσεων και ο αριθμός των αγνώστων μπορεί να μην είναι ίδιοι, είναι δυνατές τρεις περιπτώσεις:
1. Το σύστημα είναι ασυνεπές, δηλ. το σύνολο όλων των λύσεων είναι κενό. Μια αρκετά σπάνια περίπτωση που εντοπίζεται εύκολα ανεξάρτητα από τη μέθοδο επίλυσης του συστήματος.
2. Το σύστημα είναι συνεπές και καθορισμένο, δηλ. έχει ακριβώς μια λύση. Η κλασική εκδοχή, γνωστή από το σχολείο.
3. Το σύστημα είναι συμβατό και δεν έχει οριστεί, π.χ. έχει άπειρες λύσεις. Αυτή είναι η πιο δύσκολη επιλογή. Δεν αρκεί να δηλώσουμε ότι "το σύστημα έχει ένα άπειρο σύνολο λύσεων" - είναι απαραίτητο να περιγράψουμε πώς είναι διατεταγμένο αυτό το σύνολο.
Ορισμός. Μεταβλητός x iπου ονομάζεται επιτρέπεται, αν περιλαμβάνεται σε μία μόνο εξίσωση του συστήματος, και με συντελεστή 1. Με άλλα λόγια, στις υπόλοιπες εξισώσεις, ο συντελεστής της μεταβλητής x iπρέπει να είναι ίσο με μηδέν.
Εάν επιλέξουμε μία επιτρεπόμενη μεταβλητή σε κάθε εξίσωση, παίρνουμε ένα σύνολο επιτρεπόμενων μεταβλητών για ολόκληρο το σύστημα εξισώσεων. Το ίδιο το σύστημα, γραμμένο σε αυτή τη μορφή, θα ονομάζεται επίσης επιτρεπόμενο. Γενικά, ένα και το αυτό αρχικό σύστημα μπορεί να περιοριστεί σε διαφορετικά επιτρεπόμενα συστήματα, αλλά αυτό δεν μας αφορά τώρα. Ακολουθούν παραδείγματα επιτρεπόμενων συστημάτων:
Και τα δύο συστήματα επιτρέπονται ως προς τις μεταβλητές Χ 1 , Χ 3 και Χ 4 . Ωστόσο, με την ίδια επιτυχία μπορεί να υποστηριχθεί ότι το δεύτερο σύστημα επιτρέπεται σχετικά Χ 1 , Χ 3 και Χπέντε. Αρκεί να ξαναγράψουμε την τελευταία εξίσωση ως Χ 5 = Χ 4 .
Τώρα εξετάστε μια γενικότερη περίπτωση. Ας τα έχουμε όλα κμεταβλητές, εκ των οποίων rεπιτρέπονται. Τότε είναι δυνατές δύο περιπτώσεις:
1. Αριθμός επιτρεπόμενων μεταβλητών rισούται με τον συνολικό αριθμό των μεταβλητών κ: r = κ. Παίρνουμε το σύστημα από κεξισώσεις στις οποίες r = κεπιτρεπόμενες μεταβλητές. Ένα τέτοιο σύστημα είναι συνεργατικό και οριστικό, γιατί Χ 1 = σι 1 , Χ 2 = σι 2 , ..., x k = β κ;
2. Αριθμός επιτρεπόμενων μεταβλητών rμικρότερο από τον συνολικό αριθμό των μεταβλητών κ: r < κ. Το υπόλοιπο ( κ − r) οι μεταβλητές ονομάζονται ελεύθερες - μπορούν να λάβουν οποιεσδήποτε τιμές από τις οποίες υπολογίζονται εύκολα οι επιτρεπόμενες μεταβλητές.
Έτσι στα παραπάνω συστήματα οι μεταβλητές Χ 2 , Χ 5 , Χ 6 (για το πρώτο σύστημα) και Χ 2 , Χ 5 (για το δεύτερο) είναι δωρεάν. Η περίπτωση που υπάρχουν ελεύθερες μεταβλητές διατυπώνεται καλύτερα ως θεώρημα...
Πώς να λύσετε;: – Επίλυση συστήματος γραμμικών εξισώσεων με τη μέθοδο της υποκατάστασης («μέθοδος σχολείου»).
– Λύση του συστήματος με όρο προς όρο πρόσθεση (αφαίρεση) εξισώσεων συστήματος.
–Λύση του συστήματος με τύπους Cramer.
–Λύση του συστήματος με χρήση του αντίστροφου πίνακα.
–Λύση του συστήματος με τη μέθοδο Gauss.
ΚΡΑΜΕΡ
Αρχικά, εξετάστε τον κανόνα του Cramer για ένα σύστημα δύο γραμμικών εξισώσεων με δύο αγνώστους. Υπάρχουν συστήματα γραμμικών εξισώσεων με δύο μεταβλητές, που καλό είναι να λυθούν ακριβώς σύμφωνα με τον κανόνα του Cramer!
Θεωρήστε το σύστημα των εξισώσεων 
Στο πρώτο βήμα, υπολογίζουμε την ορίζουσα , ονομάζεται ο κύριος καθοριστικός παράγοντας του συστήματος.
Αν , τότε το σύστημα έχει άπειρες λύσεις ή είναι ασυνεπές (δεν έχει λύσεις). Σε αυτήν την περίπτωση, ο κανόνας του Cramer δεν θα βοηθήσει, πρέπει να χρησιμοποιήσετε Μέθοδος Gauss.
Αν , τότε το σύστημα έχει μια μοναδική λύση και για να βρούμε τις ρίζες πρέπει να υπολογίσουμε δύο ακόμη ορίζοντες: και
Στην πράξη, οι παραπάνω προσδιορισμοί μπορούν να υποδηλωθούν και με το λατινικό γράμμα.
Οι ρίζες της εξίσωσης βρίσκονται με τους τύπους:
Παράδειγμα 7
Να λύσετε ένα σύστημα γραμμικών εξισώσεων
Βλέπουμε ότι οι συντελεστές της εξίσωσης είναι αρκετά μεγάλοι, στη δεξιά πλευρά υπάρχουν δεκαδικά κλάσματα με κόμμα. Το κόμμα είναι ένας μάλλον σπάνιος επισκέπτης σε πρακτικές εργασίες στα μαθηματικά· πήρα αυτό το σύστημα από ένα οικονομετρικό πρόβλημα.
Πώς να λύσετε ένα τέτοιο σύστημα; Μπορείτε να προσπαθήσετε να εκφράσετε μια μεταβλητή σε σχέση με μια άλλη, αλλά σε αυτήν την περίπτωση, σίγουρα θα λάβετε τρομερά φανταχτερά κλάσματα, με τα οποία είναι εξαιρετικά άβολο να εργαστείτε και ο σχεδιασμός της λύσης θα φαίνεται απλώς απαίσιος. Μπορείτε να πολλαπλασιάσετε τη δεύτερη εξίσωση με 6 και να αφαιρέσετε όρο προς όρο, αλλά εδώ θα εμφανιστούν τα ίδια κλάσματα.
Τι να κάνω? Σε τέτοιες περιπτώσεις, οι φόρμουλες του Cramer έρχονται στη διάσωση.
Έτσι το σύστημα έχει μια μοναδική λύση.
;
; 
Όπως μπορείτε να δείτε, οι ρίζες αποδείχθηκαν παράλογες και βρέθηκαν κατά προσέγγιση, κάτι που είναι αρκετά αποδεκτό (και ακόμη και συνηθισμένο) για οικονομικά προβλήματα.
Δεν χρειάζονται σχόλια εδώ, καθώς η εργασία επιλύεται σύμφωνα με έτοιμους τύπους, ωστόσο, υπάρχει μια προειδοποίηση. Όταν χρησιμοποιείτε αυτή τη μέθοδο, υποχρεωτικόςΤο τμήμα της ανάθεσης είναι το ακόλουθο τμήμα: « , οπότε το σύστημα έχει μια μοναδική λύση . Διαφορετικά, ο αναθεωρητής μπορεί να σας τιμωρήσει επειδή δεν τηρείτε το θεώρημα του Cramer.
Δεν θα είναι περιττό να ελέγξετε, το οποίο είναι βολικό να πραγματοποιηθεί σε μια αριθμομηχανή: αντικαθιστούμε τις κατά προσέγγιση τιμές στην αριστερή πλευρά κάθε εξίσωσης του συστήματος. Ως αποτέλεσμα, με ένα μικρό σφάλμα, θα πρέπει να ληφθούν οι αριθμοί που βρίσκονται στη δεξιά πλευρά.
Οι τύποι του Cramer
Η μέθοδος του Cramer είναι ότι βρίσκουμε διαδοχικά αναγνωριστικό κύριου συστήματος(5.3), δηλ. μήτρα Α ορίζουσα
Και n βοηθητικές ορίζουσες D i (i= ), τα οποία λαμβάνονται από την ορίζουσα D αντικαθιστώντας την i-η στήλη με μια στήλη ελεύθερων μελών.
Οι τύποι του Cramer έχουν τη μορφή:
D × x i = D i (i = ). (5.4)
Από το (5.4), ακολουθεί ο κανόνας του Cramer, ο οποίος δίνει μια εξαντλητική απάντηση στο ερώτημα της συμβατότητας του συστήματος (5.3): εάν η κύρια ορίζουσα του συστήματος είναι μη μηδενική, τότε το σύστημα έχει μια μοναδική λύση, που καθορίζεται από τους τύπους:
Αν η κύρια ορίζουσα του συστήματος D και όλες οι βοηθητικές ορίζουσες D i = 0 (i= ), τότε το σύστημα έχει άπειρο αριθμό λύσεων. Εάν η κύρια ορίζουσα του συστήματος D = 0, και τουλάχιστον μία βοηθητική ορίζουσα είναι διαφορετική από το μηδέν, τότε το σύστημα είναι ασυνεπές.
Παράδειγμα 1.14. Λύστε το σύστημα εξισώσεων με τη μέθοδο του Cramer:
x 1 + x 2 + x 3 + x 4 = 5, x 1 + 2x 2 - x 3 + 4x 4 = -2, 2x 1 - 3x 2 - x 3 - 5x 4 = -2, 3x 1 + x 2 + 2x3 + 11x4 = 0.
Λύση.Ο κύριος προσδιοριστής αυτού του συστήματος D = 
= -142 ¹ 0, επομένως το σύστημα έχει μια μοναδική λύση. Ας υπολογίσουμε τις βοηθητικές ορίζουσες D i (i= ) που λαμβάνονται από την ορίζουσα D αντικαθιστώντας σε αυτήν μια στήλη που αποτελείται από συντελεστές στο x i με μια στήλη ελεύθερων μελών: D 1 = 
= - 142, D 2 = 
= - 284, D 3 = 
= - 426,
D4= 
= 142. Επομένως x 1 = D 1 / D = 1, x 2 = D 2 / D = 2, x 3 = D 3 / D = 3, x 4 = D 4 / D = -1, η λύση του συστήματος είναι διάνυσμα C =(1, 2, 3, -1) T .
Βασικές έννοιες συστημάτων γραμμικών εξισώσεων. Μέθοδος Gauss.
ΒΛΕΠΕ ΠΑΡΑΠΑΝΩ.
Μέθοδος Gauss-Jordan(μέθοδος πλήρους εξάλειψης αγνώστων) - μια μέθοδος που χρησιμοποιείται για την επίλυση τετραγωνικών συστημάτων γραμμικών αλγεβρικών εξισώσεων, την εύρεση του αντιστρόφου ενός πίνακα, την εύρεση των συντεταγμένων ενός διανύσματος σε μια δεδομένη βάση ή την εύρεση της κατάταξης ενός πίνακα. Η μέθοδος είναι μια τροποποίηση της μεθόδου Gauss.
Αλγόριθμος
1. Επιλέξτε την πρώτη αριστερή στήλη του πίνακα, η οποία έχει τουλάχιστον μία μη μηδενική τιμή.
2. Εάν ο ανώτατος αριθμός σε αυτήν τη στήλη είναι μηδέν, τότε αλλάξτε ολόκληρη την πρώτη σειρά του πίνακα με μια άλλη γραμμή του πίνακα, όπου δεν υπάρχει μηδέν σε αυτήν τη στήλη.
3. Όλα τα στοιχεία της πρώτης σειράς διαιρούνται με το επάνω στοιχείο της επιλεγμένης στήλης.
4. Από τις υπόλοιπες σειρές αφαιρέστε την πρώτη σειρά, πολλαπλασιαζόμενη με το πρώτο στοιχείο της αντίστοιχης σειράς, ώστε να μηδενιστεί το πρώτο στοιχείο κάθε σειράς (εκτός της πρώτης).
6. Αφού επαναλάβετε αυτή τη διαδικασία μία φορά, λαμβάνεται ένας άνω τριγωνικός πίνακας
7. Αφαιρέστε από την προτελευταία σειρά την τελευταία σειρά, πολλαπλασιαζόμενη με τον αντίστοιχο συντελεστή, ώστε μόνο το 1 στην κύρια διαγώνιο να παραμείνει στην προτελευταία σειρά.
8. Επαναλάβετε το προηγούμενο βήμα για τις επόμενες γραμμές. Ως αποτέλεσμα, λαμβάνεται ένας πίνακας ταυτότητας και μια λύση στη θέση ενός ελεύθερου διανύσματος (είναι απαραίτητο να πραγματοποιηθούν όλοι οι ίδιοι μετασχηματισμοί με αυτό).
9. Για να λάβετε τον αντίστροφο πίνακα, πρέπει να εφαρμόσετε όλες τις πράξεις με την ίδια σειρά στον πίνακα ταυτότητας.
Μέθοδος Gauss
Ιστορικά, η πρώτη, πιο κοινή μέθοδος για την επίλυση συστημάτων γραμμικών εξισώσεων είναι η μέθοδος Gauss, ή η μέθοδος διαδοχικής εξάλειψης αγνώστων. Η ουσία αυτής της μεθόδου έγκειται στο γεγονός ότι μέσω διαδοχικών εξαλείψεων αγνώστων, το δεδομένο σύστημα μετατρέπεται σε ένα κλιμακωτό (ιδίως, τριγωνικό) σύστημα ισοδύναμο με το δεδομένο. Στην πρακτική λύση ενός συστήματος γραμμικών εξισώσεων με τη μέθοδο Gauss, είναι πιο βολικό να μειωθεί σε μια σταδιακή μορφή όχι το ίδιο το σύστημα εξισώσεων, αλλά η εκτεταμένη μήτρα αυτού του συστήματος, εκτελώντας στοιχειώδεις μετασχηματισμούς στις σειρές του. Οι πίνακες που λαμβάνονται διαδοχικά κατά τη διάρκεια του μετασχηματισμού συνδέονται συνήθως με ένα σύμβολο ισοδυναμίας.
Παράδειγμα 1.13. Λύστε το σύστημα εξισώσεων χρησιμοποιώντας τη μέθοδο Gauss: x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0.
Λύση.Γράφουμε τον επαυξημένο πίνακα αυτού του συστήματος
και εκτελέστε τους ακόλουθους στοιχειώδεις μετασχηματισμούς στις σειρές του: α) αφαιρέστε την πρώτη σειρά από τη δεύτερη και την τρίτη σειρά, πολλαπλασιαζόμενες επί 3 και 2, αντίστοιχα: ~ 
;
β) πολλαπλασιάστε την τρίτη σειρά με (-5) και προσθέστε τη δεύτερη σε αυτήν: 
.
Ως αποτέλεσμα όλων αυτών των μετασχηματισμών, αυτό το σύστημα ανάγεται σε τριγωνική μορφή: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.
Από την τελευταία εξίσωση βρίσκουμε z = -1,3. Αντικαθιστώντας αυτή την τιμή στη δεύτερη εξίσωση, έχουμε y = -1,2. Περαιτέρω από την πρώτη εξίσωση παίρνουμε x = - 0,7
ΑΠΟ ΤΟ ΤΕΤΡΑΔΙΟ:
Μέθοδος Gauss
Η μέθοδος αποτελείται από δύο μέρη - προς τα εμπρός και προς τα πίσω.
Η άμεση κίνηση συνίσταται στη συμπεριφορά της επέκτασης του πίνακα SLE σε μια κλιμακωτή μορφή με τη βοήθεια στοιχειωδών μετασχηματισμών σειρών. Σε έναν βαθμιδωτό πίνακα, κάθε επόμενη σειρά έχει περισσότερα μηδενικά στην αρχή από την προηγούμενη - ή είναι μηδέν
Παράδειγμα:
Ο στοιχειώδης μετασχηματισμός των σειρών μήτρας είναι:
1) προσθέτοντας τους αριθμούς μιας σειράς του πίνακα, πολλαπλασιασμένους με κάποιο αριθμό, σε μία από τις κάτω σειρές του πίνακα.
2) Αλλάξτε δύο γραμμές κατά τόπους
Η αντίστροφη κίνηση της μεθόδου Gauss συνίσταται στη διαδοχική έκφραση ορισμένων μεταβλητών ως προς άλλες, ξεκινώντας από την κάτω μηδενική γραμμή. Το αποτέλεσμα είναι μια γενική λύση.
Μετά την εμπρός διαδρομή, υπάρχουν 3 επιλογές για τον κλιμακωτό τύπο του διευρυμένου πίνακα:
1) Κάθε επόμενη γραμμή έχει στην αρχή ακριβώς περισσότερα από ένα μηδέν περισσότερα από την προηγούμενη
Παράδειγμα:
Γράφουμε την εξίσωση γραμμή προς γραμμή και αρχίζουμε να βρίσκουμε την τιμή των μεταβλητών από την κάτω γραμμή.
4X 4 \u003d 8Þ X 4 \u003d 2
Αντικαταστήστε στην προηγούμενη εξίσωση
2X 3 -3X 4 \u003d -8 δηλ. 2X 3 -3 * 2 \u003d -8 ή 2X 3 \u003d -2, Þ X 3 \u003d -1, αντικαταστήστε τα X3 και X4 στη δεύτερη γραμμή κ.λπ. Παίρνουμε τη μοναδική λύση του SLU
2) Ο αριθμός των μη μηδενικών σειρών είναι μικρότερος από τον αριθμό των μεταβλητών. Τότε μια από τις γραμμές περιέχει μηδενικά στην αρχή τουλάχιστον 2 περισσότερα από την προηγούμενη και θεωρούμε ότι η επόμενη μη μηδενική γραμμή δεν έχει τη μορφή (0 ... 0 β) όπου ο αριθμός b=0
Για παράδειγμα:
3) Η τελευταία μη μηδενική γραμμή έχει τη μορφή (0…0/b), όπου b=0 αντιστοιχεί σε αντιφατικές ισότητες o=b, άρα το σύστημα είναι ασυμβίβαστο
Επίλυση ΣΕΛ με τη μέθοδο Gauss
2X 1 + 3X 2 + X 3 \u003d 1
4X 1 + 5X 2 + 4X 3 = 7
6Χ 1 +10Χ 2 -3Χ 3 = -10
Συνθέτουμε τον εκτεταμένο πίνακα της άμεσης κίνησης.
Υπολογισμός οριζόντων n-η σειρά:Η έννοια της ορίζουσας n-η σειρά
Χρησιμοποιώντας αυτό το άρθρο σχετικά με τους καθοριστικούς παράγοντες, θα μάθετε σίγουρα πώς να επιλύετε προβλήματα όπως τα παρακάτω:
Λύστε την εξίσωση:
και πολλά άλλα που οι δάσκαλοι λατρεύουν να σκέφτονται τόσο πολύ.
Η ορίζουσα μήτρας ή απλά η ορίζουσα παίζει σημαντικό ρόλο στην επίλυση συστημάτων γραμμικών εξισώσεων. Σε γενικές γραμμές, οι ορίζουσες επινοήθηκαν για το σκοπό αυτό. Δεδομένου ότι συχνά λέγεται και «ο προσδιοριστής μιας μήτρας», θα αναφέρουμε και εδώ πίνακες. Η μήτραείναι ένας ορθογώνιος πίνακας που αποτελείται από αριθμούς που δεν μπορούν να εναλλάσσονται. Ένας τετραγωνικός πίνακας είναι ένας πίνακας που έχει τον ίδιο αριθμό σειρών και στηλών. Μόνο ένας τετραγωνικός πίνακας μπορεί να έχει ορίζουσα.
Είναι εύκολο να κατανοήσουμε τη λογική της γραφής οριζόντων σύμφωνα με το ακόλουθο σχήμα. Ας πάρουμε ένα σύστημα δύο εξισώσεων με δύο άγνωστα γνωστά σε εσάς από το σχολείο:
Στην ορίζουσα, οι συντελεστές για αγνώστους γράφονται διαδοχικά: στην πρώτη γραμμή - από την πρώτη εξίσωση, στη δεύτερη γραμμή - από τη δεύτερη εξίσωση:
Για παράδειγμα, αν δοθεί ένα σύστημα εξισώσεων
τότε από τους συντελεστές των αγνώστων σχηματίζεται η ακόλουθη ορίζουσα:
Λοιπόν, ας υποθέσουμε ότι μας δίνεται ένας τετράγωνος πίνακας που αποτελείται από αριθμούς διατεταγμένους nσειρές (οριζόντιες σειρές) και σε nστήλες (κάθετες σειρές). Με τη βοήθεια αυτών των αριθμών, σύμφωνα με κάποιους κανόνες, που θα μελετήσουμε παρακάτω, βρίσκουν έναν αριθμό, τον οποίο καλούν καθοριστικός nη σειρά και συμβολίζονται ως εξής:
(1)
Οι αριθμοί καλούνται στοιχείαορίζουσα (1) (ο πρώτος δείκτης σημαίνει τον αριθμό της σειράς, ο δεύτερος - ο αριθμός της στήλης, στη διασταύρωση της οποίας υπάρχει ένα στοιχείο. Εγώ = 1, 2, ..., n; ι= 1, 2, ..., n). Η σειρά μιας ορίζουσας είναι ο αριθμός των σειρών και των στηλών της.
Μια νοητή ευθεία γραμμή που συνδέει τα στοιχεία της ορίζουσας για την οποία και οι δύο δείκτες είναι ίδιοι, δηλ. στοιχεία
που ονομάζεται κύρια διαγώνιο, η άλλη διαγώνιος είναι πλευρά.
Υπολογισμός οριζόντων δεύτερης και τρίτης τάξης
Ας δείξουμε πώς υπολογίζονται οι ορίζουσες των τριών πρώτων τάξεων.
Η ορίζουσα πρώτης τάξης είναι το ίδιο το στοιχείο δηλ.
Η ορίζουσα δεύτερης τάξης είναι ο αριθμός που προκύπτει ως εξής:
, (2)
Το γινόμενο των στοιχείων στην κύρια και δευτερεύουσα διαγώνιο, αντίστοιχα.
Η ισότητα (2) δείχνει ότι το γινόμενο των στοιχείων της κύριας διαγωνίου λαμβάνεται με το πρόσημο της και το γινόμενο των στοιχείων της δευτερεύουσας διαγωνίου λαμβάνεται με το αντίθετο πρόσημο .
Παράδειγμα 1Υπολογίστε ορίζοντες δεύτερης τάξης:
Λύση. Με τον τύπο (2) βρίσκουμε:
Η ορίζουσα τρίτης τάξης είναι ένας αριθμός που λαμβάνεται ως εξής:
(3)
Είναι δύσκολο να θυμηθεί κανείς αυτόν τον τύπο. Ωστόσο, υπάρχει ένας απλός κανόνας που ονομάζεται κανόνας τριγώνου , γεγονός που καθιστά εύκολη την αναπαραγωγή της έκφρασης (3). Δηλώνοντας τα στοιχεία της ορίζουσας με σημεία, συνδέουμε με ευθύγραμμα τμήματα αυτά που δίνουν τα γινόμενα των στοιχείων της ορίζουσας (Εικ. 1).
Ο τύπος (3) δείχνει ότι τα γινόμενα των στοιχείων της κύριας διαγωνίου, καθώς και τα στοιχεία που βρίσκονται στις κορυφές δύο τριγώνων, οι βάσεις των οποίων είναι παράλληλες με αυτήν, λαμβάνονται με τα σημάδια τους. με αντίθετα - τα γινόμενα των στοιχείων της δευτερεύουσας διαγωνίου, καθώς και τα στοιχεία που βρίσκονται στις κορυφές δύο τριγώνων που είναι παράλληλες με αυτήν .
Στο Σχ.1 επισημαίνονται με κόκκινο η κύρια διαγώνιος και οι βάσεις των τριγώνων που αντιστοιχούν σε αυτήν και η δευτερεύουσα διαγώνιος και οι βάσεις των τριγώνων που αντιστοιχούν σε αυτήν.
Κατά τον υπολογισμό των ορίζουσες, είναι πολύ σημαντικό, όπως και στο γυμνάσιο, να θυμάστε ότι ένας αριθμός μείον πολλαπλασιαζόμενος με έναν αριθμό οδηγεί σε ένα πρόσημο συν και ένα πρόσημο πολλαπλασιασμένο με έναν αριθμό μείον δίνει έναν αριθμό με αρνητικό πρόσημο.
Παράδειγμα 2Υπολογίστε την ορίζουσα τρίτης τάξης:
Λύση. Χρησιμοποιώντας τον κανόνα των τριγώνων, παίρνουμε
Υπολογισμός οριζόντων n-η σειρά
Επέκταση γραμμής ή στήλης ορίζουσας
Για να υπολογίσετε την ορίζουσα nμε τη σειρά, είναι απαραίτητο να γνωρίζουμε και να χρησιμοποιούμε το παρακάτω θεώρημα.
Θεώρημα Laplace.Η ορίζουσα ισούται με το άθροισμα των γινομένων των στοιχείων οποιασδήποτε σειράς και των αλγεβρικών συμπληρωμάτων τους, δηλ.
Ορισμός. Αν στην ορίζουσα nη σειρά επιλέξτε αυθαίρετα Πγραμμές και Πστήλες ( Π < n), τότε τα στοιχεία στην τομή αυτών των γραμμών και στηλών σχηματίζουν έναν πίνακα τάξης.
Ο προσδιοριστής αυτής της μήτρας ονομάζεται ανήλικος αρχική ορίζουσα. Για παράδειγμα, λάβετε υπόψη την ορίζουσα:
Ας δημιουργήσουμε έναν πίνακα από γραμμές και στήλες με ζυγούς αριθμούς:
Καθοριστικός
που ονομάζεται ανήλικοςκαθοριστικός . Έλαβε έναν ανήλικο δεύτερης τάξης. Είναι σαφές ότι μπορούν να κατασκευαστούν διάφορα ανήλικα πρώτης, δεύτερης και τρίτης τάξης.
Αν πάρουμε ένα στοιχείο και διαγράψουμε τη γραμμή και τη στήλη στην τομή των οποίων βρίσκεται στην ορίζουσα, τότε παίρνουμε μια δευτερεύουσα, που ονομάζεται ελάσσονα του στοιχείου, την οποία συμβολίζουμε με:
.
Εάν το δευτερεύον πολλαπλασιαστεί με , όπου 3 + 2 είναι το άθροισμα των αριθμών σειρών και στηλών στη τομή των οποίων βρίσκεται το στοιχείο, τότε το γινόμενο που προκύπτει ονομάζεται αλγεβρική προσθήκηστοιχείο και συμβολίζεται με,
Γενικά, η ελάσσονα ενός στοιχείου θα συμβολίζεται με , και το αλγεβρικό συμπλήρωμα με ,
(4)
Για παράδειγμα, ας υπολογίσουμε τα αλγεβρικά συμπληρώματα των στοιχείων και την ορίζουσα τρίτης τάξης:
Με τον τύπο (4) παίρνουμε 
Κατά την αποσύνθεση μιας ορίζουσας, χρησιμοποιείται συχνά η ακόλουθη ιδιότητα της ορίζουσας n-η σειρά:
εάν το γινόμενο των αντίστοιχων στοιχείων μιας άλλης γραμμής ή στήλης με σταθερό παράγοντα προστεθεί στα στοιχεία οποιασδήποτε γραμμής ή στήλης, τότε η τιμή της ορίζουσας δεν θα αλλάξει.
Παράδειγμα 4
Ας αφαιρέσουμε προκαταρκτικά τα στοιχεία της τέταρτης σειράς από την πρώτη και την τρίτη σειρά, τότε θα έχουμε
Στην τέταρτη στήλη της λαμβανόμενης ορίζουσας, τρία στοιχεία είναι μηδενικά. Επομένως, είναι πιο κερδοφόρο να επεκτείνουμε αυτόν τον καθοριστικό παράγοντα με τα στοιχεία της τέταρτης στήλης, καθώς τα τρία πρώτα προϊόντα θα είναι μηδέν. Να γιατί
Μπορείτε να ελέγξετε τη λύση με καθοριστική αριθμομηχανή σε απευθείας σύνδεση .
Και το ακόλουθο παράδειγμα δείχνει πώς ο υπολογισμός της ορίζουσας οποιασδήποτε (στην περίπτωση αυτή, της τέταρτης) τάξης μπορεί να μειωθεί στον υπολογισμό της ορίζουσας δεύτερης τάξης.
Παράδειγμα 5Υπολογίστε την ορίζουσα:
Ας αφαιρέσουμε τα στοιχεία της πρώτης σειράς από την τρίτη σειρά και ας προσθέσουμε τα στοιχεία της πρώτης σειράς στα στοιχεία της τέταρτης σειράς, τότε θα έχουμε
Στην πρώτη στήλη, όλα τα στοιχεία εκτός από το πρώτο είναι μηδενικά. Δηλαδή, η ορίζουσα μπορεί ήδη να αποσυντεθεί στην πρώτη στήλη. Αλλά πραγματικά δεν θέλουμε να υπολογίσουμε την ορίζουσα τρίτης τάξης. Επομένως, θα κάνουμε περισσότερους μετασχηματισμούς: προσθέστε τα στοιχεία της δεύτερης σειράς πολλαπλασιασμένα επί 2 στα στοιχεία της τρίτης σειράς και αφαιρέστε τα στοιχεία της δεύτερης σειράς από τα στοιχεία της τέταρτης σειράς. Ως αποτέλεσμα, η ορίζουσα, η οποία είναι ένα αλγεβρικό συμπλήρωμα, μπορεί να επεκταθεί στην πρώτη στήλη και πρέπει μόνο να υπολογίσουμε την ορίζουσα δεύτερης τάξης και να μην μπερδευτούμε στα ζώδια:
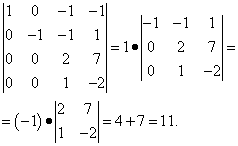
Φέρνοντας την ορίζουσα σε τριγωνική μορφή
Μια ορίζουσα όπου όλα τα στοιχεία που βρίσκονται στη μία πλευρά μιας από τις διαγωνίους είναι ίσα με μηδέν ονομάζεται τριγωνική. Η περίπτωση της δευτερεύουσας διαγωνίου μειώνεται στην περίπτωση της κύριας διαγωνίου αντιστρέφοντας τη σειρά των γραμμών ή στηλών. Μια τέτοια ορίζουσα είναι ίση με το γινόμενο των στοιχείων της κύριας διαγωνίου.
Για αναγωγή σε τριγωνική μορφή, χρησιμοποιείται η ίδια ιδιότητα της ορίζουσας nη σειρά, που χρησιμοποιήσαμε στην προηγούμενη παράγραφο: αν προσθέσουμε το γινόμενο των αντίστοιχων στοιχείων μιας άλλης γραμμής ή στήλης με σταθερό παράγοντα στα στοιχεία οποιασδήποτε γραμμής ή στήλης, τότε η τιμή της ορίζουσας δεν θα αλλάξει.
Μπορείτε να ελέγξετε τη λύση με καθοριστική αριθμομηχανή σε απευθείας σύνδεση .
Καθοριστικές ιδιότητες n-η σειρά
Στις δύο προηγούμενες παραγράφους, έχουμε ήδη χρησιμοποιήσει μία από τις ιδιότητες της ορίζουσας n-η σειρά. Σε ορισμένες περιπτώσεις, για να απλοποιήσετε τον υπολογισμό της ορίζουσας, μπορείτε να χρησιμοποιήσετε άλλες σημαντικές ιδιότητες της ορίζουσας. Για παράδειγμα, μπορεί κανείς να αναγάγει μια ορίζουσα στο άθροισμα δύο καθοριστικών παραγόντων, ο ένας ή και οι δύο μπορούν να επεκταθούν εύκολα κατά μήκος κάποιας γραμμής ή στήλης. Υπάρχουν πολλές περιπτώσεις τέτοιας απλοποίησης και το ζήτημα της χρήσης μιας ή άλλης ιδιότητας του ορίζοντα θα πρέπει να κριθεί μεμονωμένα.
Ορίζουσα μήτρας (ορίζουσα μήτρας) είναι ένας τετράγωνος πίνακας αριθμών ή μαθηματικών συμβόλων ( Δd).
Ορισμός. ορίζουσα μήτρας n×nείναι ο αριθμός:
όπου ( α 1 , α 2 ,...,α n) - μετάθεση αριθμών από 1 πριν n, N (α 1 ,α 2 ,...,α n)- ο αριθμός των αντιστροφών στη μετάθεση, η άθροιση προκύπτει σε όλες τις πιθανές μεταθέσεις της τάξης n.
Ορίζουσα μήτρας ΕΝΑαναφέρεται βασικά ως de t(A), |A|, ή ?(ΕΝΑ).
Παράμετροι, με τη βοήθεια των οποίων βρίσκεται η λύση όλων των τύπων αλγεβρικών πινάκων.
Προς την βρείτε ορίζουσα μήτραςείναι απαραίτητο να γνωρίζουμε τις βασικές ιδιότητες των πινάκων και την ακολουθία των ενεργειών κατά την επίλυση ενός πίνακα.
- Για πίνακες σειράς n=2η ορίζουσα βρίσκεται χρησιμοποιώντας τον τύπο: Δ= a11*ένα 22-ένα 12 *ένα 21
- Για πίνακες σειράς n=3η ορίζουσα βρίσκεται μέσω αλγεβρικών προσθηκών ή χρησιμοποιώντας τη μέθοδο Sarrus.
- Ένας πίνακας με διάσταση >3 αποσυντίθεται σε αλγεβρικές προσθήκες, για τις οποίες βρίσκονται οι ορίζουσες τους (ελάσσονες). Για παράδειγμα, ο προσδιοριστής ενός πίνακα 4ης τάξης υπολογίζεται μέσω επέκτασης σε γραμμές ή στήλες.
Για εύρεση ορίζουσας μήτρας, που περιέχει συναρτήσεις στον πίνακα, χρησιμοποιούνται τυπικές μέθοδοι. Για παράδειγμα, για να βρείτε την ορίζουσα ενός πίνακα τρίτης τάξης:
Ας χρησιμοποιήσουμε την επέκταση στην πρώτη γραμμή:
Δ = sin(x) × + 1× = 2sin(x) cos(x) - 2cos(x) = sin(2x) - 2cos(x)
Υπολογίστε την ορίζουσα του πίνακα.
Υπολογίστε την ορίζουσα μήτραςΥπάρχουν διάφορες μέθοδοι που παρατίθενται παρακάτω.
Ο πιο δημοφιλής τρόπος υπολογισμού της ορίζουσας ενός πίνακα είναι η μέθοδος επιλογής αλγεβρικών προσθηκών. Υπάρχει μια απλούστερη εκδοχή αυτής της μεθόδου - ο υπολογισμός της ορίζουσας χρησιμοποιώντας τον κανόνα Sarrus. Αυτές οι μέθοδοι είναι διαφορετικές κατά τον υπολογισμό της ορίζουσας ενός απλού μικρού πίνακα, και εάν χρειάζεται να υπολογίσετε έναν πίνακα μεγάλης διάστασης, τότε όπως Μέθοδοι υπολογισμού προσδιοριστικών μήτρας:
- υπολογισμός της ορίζουσας με τη μέθοδο της μείωσης της παραγγελίας,
- υπολογισμός της ορίζουσας με τη μέθοδο Gauss (με αναγωγή του πίνακα σε τριγωνική μορφή),
- υπολογισμός της ορίζουσας με τη μέθοδο της αποσύνθεσης.
Στο Excel, για τον υπολογισμό της ορίζουσας, χρησιμοποιείται η συνάρτηση = MOPRED (εύρος κελιών).