DÉTERMINANT
ou déterminant, - en mathématiques, enregistrement des nombres sous la forme d'un tableau carré, en correspondance duquel est placé un autre nombre (la « valeur » du déterminant). Très souvent, la notion de « déterminant » désigne à la fois la signification du déterminant et la forme de son enregistrement. Les déterminants vous permettent d'écrire facilement des expressions complexes qui surviennent, par exemple, lors de la résolution d'équations linéaires en géométrie analytique et en analyse mathématique. La découverte des déterminants est attribuée au mathématicien japonais S. Kova (1683) et, indépendamment, à G. Leibniz (1693). La théorie moderne remonte aux travaux de J. Binet, O. Cauchy et C. Jacobi au début du XIXe siècle. Le déterminant le plus simple est constitué de 4 nombres, appelés éléments, disposés en 2 lignes et 2 colonnes. Un tel déterminant est dit du 2ème ordre. Par exemple, c'est le déterminant

Dont la valeur est 2*5 - 3*1 (soit 10 - 3 ou 7). Dans le cas général, le déterminant du 2ème ordre s'écrit généralement sous la forme

Et sa valeur est égale à a1b2 - a2b1, où a et b sont des nombres ou des fonctions. Le déterminant de 3ème ordre est constitué de 9 éléments disposés en 3 lignes et 3 colonnes. En général, le déterminant d’ordre n se compose de n2 éléments et s’écrit généralement sous la forme

Le premier index de chaque élément indique le numéro de ligne, le second - le numéro de colonne à l'intersection de laquelle se trouve cet élément, donc aij est un élément ième ligne et la jème colonne. Souvent, un tel déterminant s’écrit |aij|. Une méthode de calcul du déterminant, presque toujours utilisée lors du calcul des déterminants d'ordre élevé, est l'expansion « mineure ». Un mineur correspondant à tout élément d'un déterminant est un déterminant d'un ordre plus petit, obtenu à partir de l'original en supprimant la ligne et la colonne à l'intersection desquelles se trouve cet élément.

Le « complément algébrique » d'un élément est son mineur, pris avec un signe plus si la somme des numéros de ligne et de colonne à l'intersection desquels se trouve l'élément est paire, et avec un signe moins si elle est impaire. Dans l'exemple ci-dessus, l'élément a2 est dans la 1ère colonne et la 2ème ligne ; la somme (1 + 2) est impaire, et donc le complément algébrique de l'élément a2 est égal à son mineur pris avec le signe moins, c'est-à-dire

La valeur du déterminant est égale à la somme des produits des éléments de n'importe quelle ligne (ou n'importe quelle colonne) par leurs compléments algébriques. Par exemple, le déterminant

développé le long de la première colonne, a la forme

et son expansion le long de la deuxième ligne a la forme

En calculant chaque mineur et en le multipliant par un coefficient, il est facile de vérifier que les deux expressions coïncident. Valeur déterminante. Sous la valeur du déterminant

Il est d'usage de comprendre la somme de tous les produits de n éléments, c'est-à-dire

Dans cette formule, la sommation s'effectue sur toutes les permutations j1, ј, jn des nombres 1, 2, ј, n et un signe plus est placé devant le terme si la permutation est paire, et un signe moins si celle-ci la permutation est étrange. Cette somme totalise exactement n ! termes dont la moitié est prise avec un signe plus, l'autre moitié avec un signe moins. Chaque terme de la somme contient un terme de chaque colonne et de chaque ligne du déterminant. On peut prouver que cette somme coïncide avec l'expression obtenue en élargissant le déterminant aux mineurs.
Propriétés du déterminant. Parmi les propriétés les plus importantes du déterminant, nous citons les suivantes. (i) Si tous les éléments d'une ligne (ou d'une colonne) sont nuls, alors la valeur du déterminant est nulle :

(ii) Si les éléments de deux lignes (ou deux colonnes) sont égaux ou proportionnels, alors la valeur du déterminant est nulle :

(iii) La valeur du déterminant ne changera pas si toutes ses lignes et colonnes sont permutées, c'est-à-dire écrivez la première ligne comme première colonne, la deuxième ligne comme deuxième colonne, etc. (cette opération est appelée transposition). Par exemple,

(iv) La valeur du déterminant ne changera pas si les éléments correspondants d'une autre ligne (ou colonne) sont ajoutés aux éléments d'une ligne (ou colonne), multipliés par un facteur arbitraire. L'exemple suivant multiplie les éléments de la deuxième ligne par -2 et les ajoute aux éléments de la première ligne :

(v) Si deux lignes (ou deux colonnes) sont permutées, le déterminant changera de signe :

(vi) Si tous les éléments d'une ligne (ou d'une colonne) contiennent un facteur commun, alors ce facteur peut être soustrait du signe déterminant :

Exemple. Calculons la valeur du déterminant du 4ème ordre suivant :

Ajoutons la 4ème ligne à la 1ère ligne :

Soustrayez la 1ère colonne de la 4ème colonne :

Multipliez la 3ème colonne par 3 et soustrayez de la 4ème colonne :

Si vous le souhaitez, les lignes et les colonnes peuvent être interverties :

Développons le déterminant dans les éléments de la quatrième rangée. Trois éléments de cette ligne sont nuls, l'élément non nul est dans la troisième colonne, et comme la somme (3 + 4) est impaire, son complément algébrique a un signe moins. En conséquence nous obtenons :

Le mineur peut être développé en éléments de la troisième ligne : deux de ses éléments sont égaux à zéro, et un élément non nul est dans la troisième colonne ; la somme (3 + 3) est paire, donc l'égalité précédente peut être continuée :

Applications. Résoudre un système d'équations

peut être obtenu en multipliant la première équation par b2, la seconde par b1, puis en soustrayant une équation de l’autre. Après avoir effectué ces opérations, on obtient

Ou si

Que

Cette notation de la solution par déterminants peut être généralisée au cas de résolution d'un système de n équations linéaires à n inconnues ; chaque déterminant sera du nième ordre. Le déterminant d'un système d'équations linéaires

volonté

Notez que si D = 0, alors les équations sont soit incohérentes, soit non indépendantes. Ainsi, le calcul préliminaire du déterminant D permet de vérifier si le système d’équations linéaires est résoluble.
Déterminants en géométrie analytique. L'équation générale d'une section conique peut être représentée comme

Déterminant

est appelé discriminant. Si D = 0, alors la courbe dégénère en une paire de lignes parallèles ou sécantes ou en un point (voir aussi SECTIONS CONIQUES). Autre exemple : l'aire d'un triangle A avec des sommets aux points (traverse - sens antihoraire) (x1, y1), (x2, y2) et (x3, y3) est donnée par

Relation entre déterminants et matrices. Une matrice est un enregistrement d'un tableau de nombres sous la forme d'un tableau rectangulaire. Les déterminants sont associés à des matrices carrées ; par exemple, déterminant matriciel

Si A, B et C sont des matrices carrées et alors |A|*|B| = |C|.
Voir aussi ALGÈBRE ABSTRAITE.
Jacobien. Si x = f (u, v), y = g (u, v) est une transformation de coordonnées, alors le déterminant

On l'appelle le déterminant jacobien ou jacobien de cette transformation. Si J n'est pas égal à 0 à un moment donné, alors dans son voisinage, les équations de transformation peuvent être résolues de manière unique par rapport à u et v, les représentant comme des fonctions de x et y.
Voir ANALYSE MATHÉMATIQUE.

Encyclopédie de Collier. - Société ouverte. 2000 .

Synonymes:

Voyez ce qu’est « QUALIFICANT » dans d’autres dictionnaires :

DÉTERMINANT, déterminant, mari. (livre). 1. Ce qui définit, exprime quelque chose. 2. Un livre utilisé comme référence pour déterminer quelque chose (scientifique). Clé végétale. Clé champignon. 3. Une expression composée de... ... Dictionnaire explicatif d'Ouchakov

- (déterminant) une expression mathématique compilée selon une certaine règle à partir de n2 nombres, utilisée dans la résolution et l'étude de systèmes d'équations algébriques du 1er degré. Le nombre n est appelé l'ordre du déterminant. Donc, un déterminant de 2ème ordre... Grand dictionnaire encyclopédique

Identifiant, hessois, mineur, déterminant Dictionnaire des synonymes russes. déterminant de nom, nombre de synonymes : 10 déterminant automatique (1) ... Dictionnaire des synonymes

DÉTERMINANT- (déterminant) une expression mathématique compilée selon une certaine règle à partir de n2 nombres, utilisée dans la résolution et l'étude de systèmes d'équations algébriques du 1er degré. Le nombre n est appelé l'ordre du déterminant. Donc, un déterminant de 2ème ordre... Grande encyclopédie polytechnique

DÉTERMINANT, moi, mari. 1. Un dispositif pour déterminer ce que n., et aussi, en général, à l'aide duquel on peut faire quoi n. déterminer avec précision, établir. Téléphone avec identification de l'appelant. O. rythme. 2. Un livre de référence pour déterminer quoi. (spécialiste.). O. les plantes... Dictionnaire explicatif d'Ojegov

- (déterminant de) matrice carrée A = ||aij|| ordre n, polynôme detA... Encyclopédie physique

déterminant- - Thèmes de télécommunications, concepts de base FR déterminant... Guide du traducteur technique

Ce terme a d'autres significations, voir Déterminant (significations). Le déterminant (ou déterminant) est l'un des concepts de base de l'algèbre linéaire. Le déterminant d'une matrice est un polynôme des éléments d'une matrice carrée (c'est-à-dire un... Wikipédia

déterminant- 3.4.6 auxiliaire : code de classe auxiliaire UDC. Source … Dictionnaire-ouvrage de référence des termes de la documentation normative et technique

JE; m.1. Livre. Ce qui est déterminé par ce qui est déterminé. Le son peut être un déterminant de la vitesse. Le principal déterminant du temps est le mouvement du Soleil dans l’espace. 2. Spécial Un guide (livre ou tableau) pour déterminer ce que... ... Dictionnaire encyclopédique

Livres

• Clé des plantes ligneuses angiospermes par fruits et graines, Sinitsyn Evgeniy Mikhailovich. Le déterminant se compose de deux parties. La première partie est un tableau d'identification des genres, et la seconde comprend des tableaux d'identification des espèces de plantes ligneuses angiospermes par...

· Déterminant carré matrices A d'ordre n ou déterminant du nième ordre est un nombre égal à une somme algébrique n! membres, dont chacun est un produit néléments matriciels pris un dans chaque ligne et dans chaque colonne avec certains signes. Le déterminant est noté ou.

Déterminant du deuxième ordre est un nombre exprimé comme suit : . Par exemple .

Déterminant du troisième ordre calculé selon la règle du triangle (règle de Sarrus) : .

Exemple. .

Commentaire. En pratique, les déterminants de troisième ordre, ainsi que ceux d'ordre supérieur, sont calculés à l'aide des propriétés des déterminants.

Propriétés des déterminants du nième ordre.

1. La valeur du déterminant ne changera pas si chaque ligne (colonne) est remplacée par une colonne (ligne) avec le même numéro - transposer.

2. Si l'une des lignes (colonnes) du déterminant est constituée de zéros, alors la valeur du déterminant est zéro.

3. Si deux lignes (colonnes) sont échangées dans le déterminant, alors la valeur absolue du déterminant ne changera pas, mais le signe changera à l'opposé.

4. Un déterminant contenant deux lignes (colonnes) identiques est égal à zéro.

5. Le facteur commun de tous les éléments d'une ligne (colonne) peut être pris au-delà du signe du déterminant.

· Mineure un élément du déterminant n-ème ordre est appelé le déterminant ( n-1)ème ordre, obtenu à partir de l'original en barrant la ligne et la colonne à l'intersection desquelles se trouve l'élément sélectionné. Désignation: .

· Complément algébrique l'élément du déterminant est appelé son mineur, pris avec le signe. Désignation : T.o. =.

6. Le déterminant d'une matrice carrée est égal à la somme des produits des éléments de n'importe quelle ligne (ou colonne) par leurs compléments algébriques ( théorème de décomposition).

7. Si chaque élément de la -ième ligne représente une somme k termes, alors le déterminant est représenté comme une somme k déterminants dans lesquels toutes les lignes à l'exception de la -ème ligne sont les mêmes que dans le déterminant d'origine, et la -ème ligne du premier déterminant est constituée des premiers termes, dans la seconde - du second, etc. Il en va de même pour les colonnes.

8. Le déterminant ne changera pas si une autre ligne (colonne) est ajoutée à l'une des lignes (colonnes), multipliée par le nombre.

Conséquence. Si une combinaison linéaire de ses autres lignes (colonnes) est ajoutée à une ligne (colonne) d'un déterminant, alors le déterminant ne changera pas.

9. Le déterminant d'une matrice diagonale est égal au produit des éléments sur la diagonale principale, c'est-à-dire

Commentaire. Le déterminant d'une matrice triangulaire est également égal au produit des éléments de la diagonale principale.

Les propriétés répertoriées des déterminants permettent de simplifier considérablement leur calcul, ce qui est particulièrement important pour les déterminants d'ordres élevés. Dans ce cas, il convient de transformer la matrice d'origine pour que la matrice transformée ait une ligne ou une colonne contenant le plus de zéros possible (lignes ou colonnes de « mise à zéro »).

Exemples. Calculons à nouveau le déterminant donné dans l'exemple précédent, en utilisant les propriétés des déterminants.

Solution: Notez que dans la première ligne il y a un facteur commun - 2, et dans la seconde - un facteur commun 3, retirons-les du signe déterminant (par propriété 5). Ensuite, nous développons le déterminant, par exemple dans la première colonne, en utilisant la propriété 6 (le théorème d'expansion).

Le plus efficace méthode de réduction du déterminant sous forme diagonale ou triangulaire . Pour calculer le déterminant d'une matrice, il suffit d'effectuer une transformation de la matrice qui ne change pas le déterminant et permet de transformer la matrice en diagonale.

En conclusion, on note que si le déterminant d'une matrice carrée est égal à zéro, alors la matrice s'appelle dégénérer (ou spécial) , sinon - non dégénéré .

1. Le déterminant ne change pas lors de la transposition.

2. Si l'une des lignes du déterminant est constituée de zéros, alors le déterminant est égal à zéro.

3. Si deux lignes du déterminant sont réorganisées, le déterminant changera de signe.

4. Un déterminant contenant deux chaînes identiques est égal à zéro.

5. Si tous les éléments d'une certaine ligne du déterminant sont multipliés par un certain nombre k, alors le déterminant lui-même sera multiplié par k.

6. Un déterminant contenant deux droites proportionnelles est égal à zéro.

7. Si tous les éléments de la i-ème ligne du déterminant sont présentés comme la somme de deux termes a i j = b j + c j (j= ), alors le déterminant est égal à la somme des déterminants pour laquelle toutes les lignes, à l'exception du i -th, sont les mêmes que dans le déterminant donné , A ième ligne dans l'un des termes, il est constitué d'éléments b j, dans l'autre - d'éléments c j.

8. Le déterminant ne change pas si les éléments correspondants d'une autre ligne sont ajoutés aux éléments d'une de ses lignes, multipliés par le même nombre.

Commentaire. Toutes les propriétés restent valides si nous prenons des colonnes au lieu de lignes.

Mineure M i j de l'élément a i j du déterminant d d'ordre n est appelé déterminant d'ordre n-1, qui est obtenu à partir de d en supprimant la ligne et la colonne contenant cet élément.

Complément algébrique l'élément a i j du déterminant d est appelé son mineur M i j , pris avec le signe (-1) i + j . Le complément algébrique d'un élément a i j sera noté A i j . Ainsi, A i j = (-1) i + j M i j .

Les méthodes de calcul pratique des déterminants, basées sur le fait qu'un déterminant d'ordre n peut être exprimé en termes de déterminants d'ordres inférieurs, sont données par le théorème suivant.

Théorème (décomposition du déterminant en ligne ou en colonne).

Le déterminant est égal à la somme des produits de tous les éléments de sa ligne (ou colonne) arbitraire par leurs compléments algébriques. En d’autres termes, il existe un développement de d dans éléments du i-ième lignes d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = )

ou la jème colonne d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).

En particulier, si tous les éléments d'une ligne (ou d'une colonne) sauf un sont nuls, alors le déterminant est égal à cet élément multiplié par son complément algébrique.

Exemple 1.4. Sans calculer le déterminant , montrer qu’il est égal à zéro. Solution. Soustrayez la première ligne de la deuxième ligne et obtenez le déterminant , égal à celui d'origine. Si on soustrait également la première de la troisième ligne, on obtient le déterminant , dans lequel les deux lignes sont proportionnelles. Ce déterminant est égal à zéro.

Exemple 1.5. Calculer le déterminant D = , en le décomposant en éléments de la deuxième colonne.

Solution. Développons le déterminant dans les éléments de la deuxième colonne :

D = une 12 Une 12 + une 22 Une 22 + une 32 Une 32 =

Exemple 1.6. Calculer le déterminant

UNE=
, dans lequel tous les éléments d'un côté de la diagonale principale sont égaux à zéro. Solution. Développons le déterminant de A le long de la première ligne : A = a 11 A 11 = . Le déterminant de droite peut être à nouveau développé le long de la première ligne, on obtient alors :

UNE=
.Et ainsi de suite. Après n étapes on arrive à l'égalité A = a 11 a 22... a nn.

3.Concepts de base des systèmes d'équations linéaires. Théorème de Cramer.

Définition. Système d'équations linéaires est un syndicat de néquations linéaires, dont chacune contient k variables. C'est écrit ainsi :

Beaucoup, rencontrant pour la première fois l'algèbre supérieure, croient à tort que le nombre d'équations doit nécessairement coïncider avec le nombre de variables. En algèbre scolaire, cela se produit généralement, mais pour l’algèbre supérieure, ce n’est généralement pas vrai.

Définition. Résoudre un système d'équations est une suite de nombres ( k 1 ,k 2 , ..., k n), qui est la solution de chaque équation du système, c'est-à-dire lors de la substitution dans cette équation au lieu de variables x 1 , x 2 , ..., xn donne l’égalité numérique correcte.

Respectivement, résoudre un système d'équations- signifie trouver l'ensemble de toutes ses solutions ou prouver que cet ensemble est vide. Le nombre d'équations et le nombre d'inconnues pouvant ne pas coïncider, trois cas sont possibles :

1. Le système est incohérent, c'est-à-dire l'ensemble de toutes les solutions est vide. Il s’agit d’un cas assez rare qui est facilement détecté quelle que soit la méthode utilisée pour résoudre le système.

2. Le système est cohérent et défini, c'est-à-dire a exactement une solution. La version classique, bien connue depuis l'école.

3. Le système est cohérent et indéfini, c'est-à-dire a une infinité de solutions. C'est l'option la plus difficile. Il ne suffit pas d'indiquer que « le système possède un ensemble infini de solutions », il faut décrire comment cet ensemble est structuré.

Définition. Variable x je appelé permis, s'il est inclus dans une seule équation du système, et avec un coefficient de 1. En d'autres termes, dans les équations restantes le coefficient de la variable x je doit être égal à zéro.

Si nous sélectionnons une variable autorisée dans chaque équation, nous obtenons un ensemble de variables autorisées pour l'ensemble du système d'équations. Le système lui-même, écrit sous cette forme, sera également appelé résolu. D'une manière générale, un même système original peut être réduit à différents systèmes autorisés, mais pour l'instant cela ne nous préoccupe pas. Voici des exemples de systèmes autorisés :

Les deux systèmes sont à résolution variable x 1 , x 3 et x 4. Cependant, avec le même succès, on peut affirmer que le deuxième système est relativement autorisé x 1 , x 3 et x 5. Il suffit de réécrire la toute dernière équation sous la forme x 5 = x 4 .

Considérons maintenant un cas plus général. Puissions-nous avoir tout k variables, dont r sont autorisés. Deux cas sont alors possibles :

1. Nombre de variables autorisées régal au nombre total de variables k: r = k. On obtient le système de kéquations dans lesquelles r = k variables autorisées. Un tel système est conjoint et définitif, car x 1 = b 1 , x 2 = b 2 , ..., xk = bb;

2. Nombre de variables autorisées r moins nombre total variables k: r < k. Le reste ( k − r) les variables sont dites libres - elles peuvent prendre n'importe quelle valeur à partir de laquelle les variables autorisées peuvent être facilement calculées.

Ainsi, dans les systèmes ci-dessus, les variables x 2 , x 5 , x 6 (pour le premier système) et x 2 , x 5 (pour le deuxième) sont gratuits. Le cas où il existe des variables libres est mieux formulé sous forme de théorème...

Comment résoudre ? : – Résoudre un système d’équations linéaires par la méthode de substitution (« méthode scolaire »).
– Résoudre le système par addition (soustraction) terme par terme des équations du système.
–Solution du système utilisant les formules de Cramer.
–Résolution du système à l'aide d'une matrice inverse.
–Résolution du système par la méthode gaussienne.

KRAMER

Considérons d’abord la règle de Cramer pour un système de deux équations linéaires à deux inconnues. Il existe des systèmes d’équations linéaires à deux variables qu’il est conseillé de résoudre en utilisant la règle de Cramer !

Considérons le système d'équations

Dans un premier temps, on calcule le déterminant, on l'appelle principal déterminant du système.

Si , alors le système a une infinité de solutions ou est incohérent (n’a pas de solutions). Dans ce cas, la règle de Cramer n'aidera pas, vous devez utiliser Méthode gaussienne.

Si , alors le système a une solution unique, et pour trouver les racines, nous devons calculer deux déterminants supplémentaires : et

En pratique, les qualificatifs ci-dessus peuvent également être désignés par une lettre latine.

On trouve les racines de l'équation à l'aide des formules :

Exemple 7

Résoudre un système d'équations linéaires

On voit que les coefficients de l'équation sont assez grands ; sur le côté droit il y a des fractions décimales avec une virgule. La virgule est un invité assez rare dans les tâches pratiques de mathématiques ; j'ai tiré ce système d'un problème économétrique.

Comment résoudre un tel système ? Vous pouvez essayer d'exprimer une variable en termes d'une autre, mais dans ce cas, vous vous retrouverez probablement avec des fractions fantaisistes terribles avec lesquelles il est extrêmement gênant de travailler, et la conception de la solution aura l'air tout simplement terrible. Vous pouvez multiplier la deuxième équation par 6 et soustraire terme par terme, mais les mêmes fractions apparaîtront ici aussi.

Ce qu'il faut faire? Dans de tels cas, les formules de Cramer viennent à la rescousse.

Cela signifie que le système a une solution unique.

;

;

Comme vous pouvez le constater, les racines se sont révélées irrationnelles et ont été trouvées approximativement, ce qui est tout à fait acceptable (et même banal) pour les problèmes d'économétrie.

Les commentaires ne sont pas nécessaires ici, puisque la tâche est résolue à l'aide de formules toutes faites. Il y a cependant une mise en garde. Lorsque vous utilisez cette méthode, obligatoire Un fragment de la conception de la tâche est le fragment suivant : « , ce qui signifie que le système a une solution unique" . Sinon, le critique pourrait vous punir pour manque de respect envers le théorème de Cramer.

Il ne serait pas superflu de vérifier, ce qui peut être facilement effectué sur une calculatrice : on substitue des valeurs approximatives dans le côté gauche de chaque équation du système. En conséquence, avec une petite erreur, vous devriez obtenir des nombres qui se trouvent du bon côté.

Les formules de Cramer

La méthode de Cramer consiste à trouver séquentiellement principal déterminant du système(5.3), c'est-à-dire déterminant de la matrice A

Et n déterminants auxiliaires D i (i= ), qui sont obtenus à partir du déterminant D en remplaçant la i-ème colonne par une colonne de termes libres.

Les formules de Cramer ressemblent à :

D × x je = D je (je = ). (5.4)

De (5.4) découle la règle de Cramer, qui donne une réponse exhaustive à la question de la compatibilité du système (5.3) : si le déterminant principal du système est non nul, alors le système a une solution unique, déterminée par les formules :

Si le déterminant principal du système D et tous les déterminants auxiliaires D i = 0 (i= ), alors le système a un nombre infini de solutions. Si le déterminant principal du système D = 0 et qu'au moins un déterminant auxiliaire est différent de zéro, alors le système est incohérent.

Exemple 1.14. Résolvez le système d'équations en utilisant la méthode Cramer :

x 1 + x 2 + x 3 + x 4 = 5, x 1 + 2x 2 - x 3 + 4x 4 = -2, 2x 1 - 3x 2 - x 3 - 5x 4 = -2, 3x 1 + x 2 + 2x3 + 11x4 = 0.

Solution. Le principal déterminant de ce système est D = = -142 ¹ 0, ce qui signifie que le système a une solution unique. Calculons les déterminants auxiliaires D i (i= ), obtenus à partir du déterminant D en y remplaçant la colonne constituée des coefficients de x i par une colonne de termes libres : D 1 = = - 142, J 2 = = - 284, J 3 = = - 426,

J4 = = 142. D'où x 1 = D 1 /D = 1, x 2 = D 2 /D = 2, x 3 = D 3 /D = 3, x 4 = D 4 /D = -1, la solution du système est le vecteur C =(1, 2, 3, -1) T .

Concepts de base des systèmes d'équations linéaires. Méthode gaussienne.

VOIR CI-DESSUS.

Méthode Gauss-Jordan(méthode d'élimination complète des inconnues) - une méthode utilisée pour résoudre des systèmes quadratiques d'équations algébriques linéaires, trouver l'inverse d'une matrice, trouver les coordonnées d'un vecteur dans une base donnée ou trouver le rang d'une matrice. La méthode est une modification de la méthode de Gauss.

Algorithme

1. Sélectionnez la première colonne à gauche de la matrice, qui contient au moins une valeur non nulle.

2. Si le nombre le plus haut de cette colonne est zéro, échangez toute la première ligne de la matrice avec une autre ligne de la matrice où il n'y a pas de zéro dans cette colonne.

3. Tous les éléments de la première ligne sont divisés par l'élément supérieur de la colonne sélectionnée.

4. Des lignes restantes, soustrayez la première ligne, multipliée par le premier élément de la ligne correspondante, afin d'obtenir zéro comme premier élément de chaque ligne (sauf le premier).

6. Après avoir répété cette procédure une fois, la matrice triangulaire supérieure est obtenue

7. Soustrayez de l'avant-dernière ligne la dernière ligne, multipliée par le coefficient correspondant, de sorte que dans l'avant-dernière ligne il n'en reste que 1 sur la diagonale principale.

8. Répétez l'étape précédente pour les lignes suivantes. Du coup, on obtient une matrice identité et une solution à la place du vecteur libre (il faut effectuer les mêmes transformations avec).

9. Pour obtenir la matrice inverse, vous devez appliquer toutes les opérations dans le même ordre à la matrice identité.

Méthode Gauss

Historiquement, la première méthode, la plus courante, pour résoudre des systèmes d'équations linéaires est la méthode de Gauss, ou la méthode d'élimination séquentielle des inconnues. L'essence de cette méthode est que par élimination successive d'inconnues ce système se transforme en un système pas à pas (en particulier triangulaire) équivalent à celui-ci. Lors de la résolution pratique d'un système d'équations linéaires à l'aide de la méthode gaussienne, il est plus pratique de réduire à une forme pas à pas non pas le système d'équations lui-même, mais la matrice étendue de ce système, effectuant des transformations élémentaires sur ses lignes. Les matrices séquentielles obtenues lors de la transformation sont généralement reliées par un signe d'équivalence.

Exemple 1.13. Résolvez le système d'équations en utilisant la méthode de Gauss : x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0.

Solution.Écrivons la matrice étendue de ce système

et effectuer les transformations élémentaires suivantes sur ses lignes : a) de ses deuxième et troisième lignes, soustraire la première, multipliée respectivement par 3 et 2 : ~ ;

b) multipliez la troisième ligne par (-5) et ajoutez-y la deuxième : .

Suite à toutes ces transformations, ce système se réduit à une forme triangulaire : x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.

À partir de la dernière équation, nous trouvons z = -1,3. En substituant cette valeur dans la deuxième équation, nous avons y = -1,2. Ensuite, à partir de la première équation, nous obtenons x = - 0,7

À PARTIR DU CARNET:

Méthode Gauss

La méthode se compose de deux parties : avant et arrière.

L'approche directe consiste à étendre la matrice SLN sous une forme échelonnée à l'aide de transformations de lignes élémentaires. Dans une matrice pas à pas, chaque ligne suivante a plus de zéros non significatifs que la précédente - ou elle est nulle

Exemple:

Les transformations élémentaires de lignes de matrice sont :

1) ajouter les nombres d'une ligne de la matrice, multipliés par un certain nombre, à l'une des lignes inférieures de la matrice.

2) Échangez deux lignes

L’inverse de la méthode gaussienne consiste à exprimer séquentiellement certaines variables par rapport à d’autres, en partant de la ligne zéro inférieure. Le résultat est une solution générale.

Après un trait direct, 3 options pour la forme étagée de la matrice étendue sont possibles :

1) Chaque ligne suivante a exactement un zéro de plus au début que la précédente

Exemple:

Nous écrivons l'équation ligne par ligne et commençons à trouver les valeurs des variables à partir de la ligne du bas.

4Х 4 =8Þ × 4 =2

Remplacer dans l'équation précédente

2X 3 -3X 4 = -8 soit 2X 3 -3 * 2=-8 ou 2X 3 =-2, Þ X 3 =-1, remplacer X3 et X4 dans la deuxième ligne, etc. Nous obtenons la seule solution à SLU

2) Le nombre de lignes non nulles est inférieur au nombre de variables. Alors une des lignes contient au début des zéros au moins 2 de plus que la précédente et on suppose que la ligne suivante non nulle n'a pas la forme (0...0 b) où le nombre b=0

Par exemple:

3) La dernière ligne non nulle a la forme (0...0/b), où b=0 elle correspond aux égalités contradictoires o=b, donc le système est incompatible

Résolution des SLE à l'aide de la méthode gaussienne

2X1 +3X2 +X3 =1

4X1 +5X2 +4X3 =7

6X1 +10X2 -3X3 = -10

Nous composons une matrice de mouvement vers l’avant étendue.

Calcul des déterminants n-ème ordre :

La notion de déterminant n-ième commande

Grâce à cet article sur les déterminants, vous apprendrez certainement à résoudre des problèmes tels que les suivants :

Résolvez l'équation :

et bien d’autres que les enseignants adorent proposer.

Le déterminant d'une matrice, ou simplement le déterminant, joue un rôle important dans la résolution de systèmes d'équations linéaires. En général, les déterminants ont été inventés à cet effet. Puisqu’ils disent souvent aussi « déterminant d’une matrice », nous mentionnerons également ici les matrices. Matrice est une table rectangulaire composée de nombres qui ne peuvent pas être échangés. Une matrice carrée est un tableau qui comporte le même nombre de lignes et de colonnes. Seule une matrice carrée peut avoir un déterminant.

Il est facile de comprendre la logique de l’enregistrement des déterminants en utilisant le schéma suivant. Prenons un système de deux équations à deux inconnues, familier à l’école :

Dans le déterminant, les coefficients des inconnues sont écrits séquentiellement : dans la première ligne - à partir de la première équation, dans la deuxième ligne - à partir de la deuxième équation :

Par exemple, si on lui donne un système d'équations

alors le déterminant suivant est formé à partir des coefficients des inconnues :

Alors, donnons-nous un tableau carré composé de nombres disposés en n lignes (lignes horizontales) et dans n colonnes (lignes verticales). A l'aide de ces nombres, selon certaines règles que nous étudierons ci-dessous, ils trouvent le nombre, qui s'appelle déterminant n-ième ordre et noté comme suit :

(1)

Les numéros sont appelés éléments déterminant (1) (le premier indice signifie le numéro de ligne, le second – le numéro de colonne à l'intersection de laquelle se trouve l'élément ; je = 1, 2, ..., n; j= 1, 2, ..., n). L'ordre d'un déterminant est le nombre de ses lignes et colonnes.

Une ligne droite imaginaire reliant les éléments du déterminant pour laquelle les deux indices sont identiques, c'est-à-dire éléments

appelé diagonale principale, une autre diagonale – côté.

Calcul des déterminants du deuxième et du troisième ordre

Montrons comment sont calculés les déterminants des trois premiers ordres.

Le déterminant du premier ordre est l'élément lui-même, c'est-à-dire

Le déterminant du second ordre est le nombre obtenu comme suit :

, (2)

Le produit d'éléments situés respectivement sur les diagonales principale et secondaire.

L'égalité (2) montre que le produit des éléments de la diagonale principale est pris avec son propre signe, et le produit des éléments de la diagonale secondaire est pris avec le signe opposé .

Exemple 1. Calculer les déterminants du second ordre :

Solution. En utilisant la formule (2) on trouve :

Un déterminant du troisième ordre est un nombre obtenu comme suit :

(3)

Il est difficile de retenir cette formule. Cependant, il existe une règle simple appelée règle triangulaire , ce qui facilite la reproduction de l'expression (3). En désignant les éléments du déterminant par des points, on relie par des segments de droite ceux d'entre eux qui donnent le produit des éléments du déterminant (Fig. 1).

La formule (3) montre que les produits des éléments de la diagonale principale, ainsi que les éléments situés aux sommets de deux triangles dont les bases lui sont parallèles, sont pris avec leurs signes ; avec des éléments opposés - le produit des éléments de la diagonale latérale, ainsi que des éléments situés aux sommets de deux triangles qui lui sont parallèles .

Sur la figure 1, la diagonale principale et les bases correspondantes des triangles et la diagonale secondaire et les bases correspondantes des triangles sont surlignées en rouge.

Lors du calcul des déterminants, il est très important, comme au lycée, de se rappeler qu'un nombre avec un signe moins multiplié par un nombre avec un signe moins donne un nombre avec un signe plus, et un nombre avec un signe plus multiplié par un un nombre avec un signe moins donne un nombre avec un signe moins.

Exemple 2. Calculez le déterminant du troisième ordre :

Solution. En utilisant la règle du triangle, on obtient

Calcul des déterminants n-ième commande

Développer le déterminant par ligne ou colonne

Pour calculer le déterminant n-ème ordre, vous devez connaître et utiliser le théorème suivant.

Théorème de Laplace. Le déterminant est égal à la somme des produits des éléments de n'importe quelle ligne et de leurs compléments algébriques, c'est-à-dire

Définition. Si dans le déterminant n commander - choisir arbitrairement p lignes et p colonnes ( p < n), alors les éléments situés à l'intersection de ces lignes et colonnes forment une matrice d'ordre.

Le déterminant de cette matrice s'appelle mineure le déterminant originel. Par exemple, considérons le déterminant :

Construisons une matrice à partir de lignes et de colonnes avec des nombres pairs :

Déterminant

appelé mineure déterminant Nous avons eu un mineur du deuxième ordre. Il est clair qu’à partir de là on peut construire différents mineurs du premier, du deuxième et du troisième ordre.

Si nous prenons un élément et barrons dans le déterminant la ligne et la colonne à l'intersection desquelles il se trouve, nous obtenons un mineur appelé élément mineur, que nous désignons par :

.

Si le mineur est multiplié par , où 3 + 2 est la somme des numéros de ligne et de colonne à l'intersection desquels se trouve un élément, alors le produit résultant est appelé complément algébriqueélément et est désigné par

En général, on désignera le mineur d'un élément, et le complément algébrique,

(4)

Par exemple, calculons les compléments algébriques des éléments et du déterminant du troisième ordre :

En utilisant la formule (4) on obtient

Lors de la décomposition d'un déterminant, la propriété suivante du déterminant est souvent utilisée n-ème ordre :

Si le produit des éléments correspondants d'une autre ligne ou colonne est ajouté aux éléments d'une ligne ou d'une colonne par un facteur constant, alors la valeur du déterminant ne changera pas.

Exemple 4.

Tout d’abord, soustrayez les éléments de la quatrième ligne des première et troisième lignes, nous aurons alors

La quatrième colonne du déterminant résultant contient trois éléments – des zéros. Par conséquent, il est plus rentable d'étendre ce déterminant aux éléments de la quatrième colonne, puisque les trois premiers produits seront des zéros. C'est pourquoi

Vous pouvez vérifier la solution en utilisant calculateur de déterminant en ligne .

Et l’exemple suivant montre comment le calcul d’un déterminant de n’importe quel ordre (dans ce cas, le quatrième) peut être réduit au calcul d’un déterminant de second ordre.

Exemple 5. Calculez le déterminant :

Soustrayons les éléments de la première ligne de la troisième ligne, et ajoutons les éléments de la première ligne aux éléments de la quatrième ligne, nous aurons alors

Dans la première colonne, tous les éléments sauf le premier sont des zéros. Autrement dit, le déterminant peut déjà être étendu à la première colonne. Mais nous ne voulons vraiment pas calculer le déterminant du troisième ordre. Par conséquent, nous ferons encore quelques transformations : aux éléments de la troisième ligne nous ajouterons les éléments de la deuxième ligne, multipliés par 2, et des éléments de la quatrième ligne nous soustrairons les éléments de la deuxième ligne. De ce fait, le déterminant, qui est un complément algébrique, peut lui-même être développé le long de la première colonne et il suffit de calculer le déterminant du second ordre et de ne pas se confondre dans les signes :

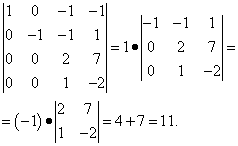
Réduire le déterminant à la forme triangulaire

Un déterminant où tous les éléments situés d'un côté d'une des diagonales sont égaux à zéro est appelé triangulaire. En inversant l'ordre des lignes ou des colonnes, le cas d'une diagonale secondaire se réduit au cas de la diagonale principale. Ce déterminant est égal au produit des éléments de la diagonale principale.

Pour réduire à la forme triangulaire, la même propriété du déterminant est utilisée n-ème ordre, que nous avons appliqué dans le paragraphe précédent : si le produit des éléments correspondants d'une autre ligne ou colonne par un facteur constant est ajouté aux éléments d'une ligne ou d'une colonne, alors la valeur du déterminant ne changera pas.

Vous pouvez vérifier la solution en utilisant calculateur de déterminant en ligne .

Propriétés du déterminant n-ième commande

Dans les deux paragraphes précédents nous avons déjà utilisé une des propriétés du déterminant n-ième ordre. Dans certains cas, pour simplifier le calcul du déterminant, vous pouvez utiliser d'autres propriétés importantes du déterminant. Par exemple, on peut réduire un déterminant à la somme de deux déterminants, dont l’un ou les deux peuvent être facilement développés dans une ligne ou une colonne. Il existe de nombreux cas d'une telle simplification, et la question de l'utilisation de l'une ou l'autre propriété du déterminant doit être résolue individuellement.

Déterminant matriciel (déterminant matriciel) est un tableau carré de nombres ou de symboles mathématiques ( Δd).

Définition. Déterminant matriciel n×n est le numéro :

Où ( α 1 , α 2 ,...,α n) - permutation des nombres de 1 à n, N (α 1 ,α 2 ,...,α n)- nombre d'inversions dans une permutation, la sommation se produit sur toutes les permutations d'ordre possibles n.

Déterminant matriciel UN généralement appelé de t(UNE), |UNE|, ou ?(UN).

Paramètres utilisés pour trouver des solutions à tous les types de matrices algébriques.

À trouver le déterminant de la matrice vous devez connaître les propriétés de base des matrices et la séquence d'actions lors de la résolution d'une matrice.

1. Pour les matrices de commande n=2 le déterminant se trouve à l'aide de la formule : Δ= un 11*un 22 -un 12*un 21
2. Pour les matrices de commande n=3 le déterminant est trouvé par additions algébriques ou par la méthode de Sarrus.
3. Une matrice de dimension >3 est décomposée en compléments algébriques, pour lesquels on trouve leurs propres déterminants (mineurs). Par exemple, le déterminant d'une matrice du 4ème ordre est calculé par développement de lignes ou de colonnes.

Pour trouver le déterminant de la matrice, qui contient des fonctions dans la matrice, des méthodes standard sont utilisées. Par exemple, trouvez le déterminant d’une matrice du troisième ordre :

Utilisons le développement le long de la première ligne :

Δ = sin(x) × + 1× = 2sin(x) cos(x) - 2cos(x) = sin(2x) - 2cos(x)

Calculez le déterminant de la matrice.

Calculer le déterminant d'une matrice possible en utilisant plusieurs méthodes, qui seront énumérées ci-dessous.

La méthode la plus populaire pour calculer le déterminant d'une matrice est la méthode de sélection des compléments algébriques. Il existe une version plus simple de cette méthode : calculer le déterminant à l'aide de la règle de Sarrus. Ces méthodes sont excellentes pour calculer le déterminant d'une petite matrice simple, et si vous devez calculer une matrice de grande dimension, les éléments suivants peuvent être utilisés méthodes de calcul du déterminant d'une matrice:

• calculer le déterminant par la méthode de réduction d'ordre,
• calculer le déterminant par la méthode gaussienne (en réduisant la matrice à une forme triangulaire),
• calcul du déterminant par la méthode de décomposition.

Dans Excel, la fonction =MOPRED(cell range) est utilisée pour calculer le déterminant.