DÖNTŐ
vagy determináns, - a matematikában a számok feljegyzése négyzet alakú táblázat formájában, amelynek megfelelően egy másik szám kerül (a determináns "értéke"). A "determináns" kifejezés nagyon gyakran a determináns jelentését és jelölésének formáját is jelenti. A determinánsok lehetővé teszik olyan összetett kifejezések kényelmes írását, amelyek például lineáris egyenletek megoldása során merülnek fel az analitikus geometriában és a matematikai elemzésben. A determinánsok felfedezése S. Kova japán matematikusnak (1683) és egymástól függetlenül G. Leibniznek (1693) tulajdonítható. A modern elmélet J. Binet, O. Cauchy és C. Jacobi műveire nyúlik vissza a 19. század elején. A legegyszerűbb determináns 4 számból, úgynevezett elemekből áll, amelyek 2 sorban és 2 oszlopban vannak elrendezve. Az ilyen determinánsról azt mondják, hogy 2. rendű. Például ez a meghatározó

Ennek értéke 2*5 - 3*1 (azaz 10 - 3 vagy 7). Általános esetben a 2. rendű determinánst általában a formába írjuk

És értéke a1b2 - a2b1, ahol a és b számok vagy függvények. A 3. rendű determináns 9 elemből áll, amelyek 3 sorban és 3 oszlopban vannak elrendezve. Általában az n-edrendű determináns n2 elemből áll, és általában így írják

Az egyes elemek első indexe a sor számát jelzi, a második - annak az oszlopnak a számát, amelynek metszéspontjában ez az elem található, tehát az aij az i-edik sor és a j-edik oszlop eleme. Az ilyen determinánst gyakran |aij|-ként írják le. A determináns kiszámításának egyik módszere, amelyet a magasabb rendű determinánsok számításánál szinte mindig használnak, a "kisebb" bővítés. A determináns bármely elemének megfelelő minor egy 1-nél kisebb rendű determináns, amelyet az eredetiből úgy kapunk, hogy töröljük azt a sort és oszlopot, amelynek metszéspontjában ez az elem áll. Például a determináns a2 elemének megfelelő moll

Egy elem "algebrai komplementere" a minor, pluszjellel, ha annak a sornak és oszlopnak az összege, amelynek metszéspontjában az elem áll, páros, mínuszjellel, ha páratlan. A fenti példában az a2 elem az 1. oszlopban és a 2. sorban található; az összeg (1 + 2) páratlan, ezért az a2 elem algebrai komplementere egyenlő a mínusz előjellel vett molljával, azaz.

A determináns értéke megegyezik bármely sor (vagy bármely oszlop) elemeinek és algebrai komplementereik szorzatának összegével. Például a determináns

az első oszlop fölé kibontva az űrlapot kapja

a második sorban lévő bővítése pedig a formát

Az egyes minorok kiszámításával és egy együtthatóval való megszorzásával könnyen ellenőrizhető, hogy mindkét kifejezés azonos-e. A determináns értéke. A determináns értéke alatt

Szokás érteni n elem összes szorzatának összegét, azaz.

Ebben a képletben az 1, 2, ј, n számok összes j1, ј, jn permutációján összegzés történik, és a tagot pluszjel előzi meg, ha a permutáció páros, és mínusz előjel, ha ez a permutáció páratlan. . Egy ilyen összeg pontosan n! tagjai, amelyek felét pluszjellel, felét - mínuszjellel veszik. Minden összegtag minden oszlopból és a determináns sorából egy tagot tartalmaz. Bizonyítható, hogy ez az összeg egybeesik a determináns kiskorúak kibővítésével kapott kifejezéssel.
Meghatározó tulajdonságok. A determináns legfontosabb tulajdonságai közül a következőket említjük. (i) Ha bármely sor (vagy bármely oszlop) minden eleme nulla, akkor a determináns értéke is nulla:

(ii) Ha két sor (vagy két oszlop) elemei egyenlőek vagy arányosak, akkor a determináns értéke nulla:

(iii) A determináns értéke nem változik, ha minden sorát és oszlopát felcseréljük, azaz. írja az első sort az első oszlopnak, a második sort a második oszlopnak, és így tovább. (ezt a műveletet transzponálásnak nevezik). Például,

(iv) A determináns értéke nem változik, ha egy sor (vagy oszlop) elemeihez hozzáadjuk egy másik sor (vagy oszlop) megfelelő elemeit tetszőleges tényezővel megszorozva. A következő példa a második sor elemeit megszorozza -2-vel, és hozzáadja őket az első sor elemeihez:

(v) Ha két sort (vagy két oszlopot) felcserélünk, a determináns előjelet vált:

(vi) Ha egy sor (vagy egy oszlop) minden eleme közös tényezőt tartalmaz, akkor ez a tényező kivehető a determináns előjeléből:

Példa. Számítsa ki a következő 4. rendű determináns értékét:

Adjuk hozzá a 4. sort az 1. sorhoz:

Vonjuk ki az 1. oszlopot a 4. oszlopból:

Szorozzuk meg a 3. oszlopot 3-mal, és vonjuk ki a 4. oszlopból:

Ha szeretné, felcserélheti a sorokat és oszlopokat:

Bővítsük ki a determinánst a negyedik sor elemeivel. Ennek a sornak három eleme egyenlő nullával, a nem nulla elem a harmadik oszlopban található, és mivel az összeg (3 + 4) páratlan, algebrai komplementere mínusz előjelű. Ennek eredményeként a következőket kapjuk:

A moll a harmadik sor elemeire bontható: két eleme egyenlő nullával, a harmadik oszlopban pedig egy nem nulla elem található; az összeg (3 + 3) páros, így az előző egyenlőség folytatható:

Alkalmazások. Egyenletrendszer megoldása

úgy kaphatjuk meg, hogy az első egyenletet megszorozzuk b2-vel, a másodikat b1-gyel, majd az egyik egyenletet kivonjuk a másikból. Ezen műveletek elvégzésével azt kapjuk

Vagy ha

azután

A megoldásnak a determinánsok segítségével történő ilyen rögzítése lehetővé teszi az általánosítást egy n lineáris egyenletrendszer megoldásának esetére, n ismeretlennel; minden determináns n-edik rendű lesz. Lineáris egyenletrendszer determinánsa

akarat

Vegye figyelembe, hogy ha D = 0, akkor az egyenletek vagy inkonzisztensek vagy nem függetlenek. Ezért a D determináns előzetes számítása lehetővé teszi annak ellenőrzését, hogy a lineáris egyenletrendszer megoldható-e.
Determinánsok az analitikus geometriában. A kúpszelet általános egyenlete a következőképpen ábrázolható

Döntő

diszkriminánsnak nevezzük. Ha D = 0, akkor a görbe párhuzamos vagy metsző egyenesek párjává, vagy ponttá degenerálódik (lásd még KÚPMETSZET). Egy másik példa: az A háromszög területét, amelynek csúcsai a pontokban (kerülés - az óramutató járásával ellentétes irányban) (x1, y1), (x2, y2) és (x3, y3) találhatók

Determinánsok kapcsolata mátrixokkal. A mátrix egy számtömb rekordja téglalap alakú táblázat formájában. A determinánsok négyzetmátrixokhoz kapcsolódnak; például mátrix determináns

Ha A, B és С négyzetmátrixok, és akkor |A|*|B| = |C|.
Lásd még ALGEBRA AZ ABSZTRAKT.
Jacobi. Ha x = f (u, v), y = g (u, v) koordináta transzformáció, akkor a determináns

Ezt az átalakulást Jacobi vagy Jacobi determinánsának nevezik. Ha J egy ponton nem egyenlő 0-val, akkor a szomszédságában a transzformációs egyenletek egyedileg megoldhatók u és v vonatkozásában, x és y függvényeiként ábrázolva őket.
Lásd: MATEMATIKAI ELEMZÉS.

Collier Encyclopedia. - Nyitott társadalom. 2000 .

Szinonimák:

Nézze meg, mi a "DETERMINANT" más szótárakban:

MEGHATÁROZÓ, determináns, férfi. (könyv). 1. Ami meghatároz, kifejez valamit. 2. Egy könyv, amely referenciaként szolgál valami (tudományos) meghatározásában. Növény azonosítás. Gomba útmutató. 3. Egy kifejezés, amely ... ... Usakov magyarázó szótára

- (determináns) n2 számból meghatározott szabály szerint összeállított matematikai kifejezés, amelyet I. fokú algebrai egyenletrendszerek megoldásában és tanulmányozásában használnak. Az n számot a determináns sorrendjének nevezzük. Tehát a 2. rend meghatározója... Nagy enciklopédikus szótár

Azonosító, hesszi, moll, meghatározó Orosz szinonimák szótára. főnév meghatározó, szinonimák száma: 10 autodeterminer (1) … Szinonima szótár

DÖNTŐ- (determináns) n2 számból meghatározott szabály szerint összeállított matematikai kifejezés, amelyet I. fokú algebrai egyenletrendszerek megoldásában és tanulmányozásában használnak. Az n számot a determináns sorrendjének nevezzük. Tehát a 2. rend meghatározója... Nagy Politechnikai Enciklopédia

MEGHATÁROZÓ, én, férj. 1. Eszköz annak meghatározására, hogy mi n., valamint általában is, melynek segítségével lehet n. pontosan meghatározni. Telefon hívóazonosítóval. O. ritmus. 2. Egy könyv referenciaként annak meghatározásához, hogy mi n. (szakember.). O. növények... Ozhegov magyarázó szótára

- (determinánsa) a négyzetmátrix A = ||aij|| n sorrend, detA polinom… Fizikai Enciklopédia

döntő- - Távközlési témák, alapfogalmak EN meghatározó ... Műszaki fordítói kézikönyv

Ennek a kifejezésnek más jelentései is vannak, lásd: Determináns (jelentések). A determináns (vagy determináns) a lineáris algebra egyik alapfogalma. A mátrix determináns egy polinom egy négyzetmátrix elemeiben (vagyis olyan, hogy y ... Wikipédia

döntő- 3.4.6 minősítő (kiegészítő): UDC segédosztálykód. Forrás … A normatív és műszaki dokumentáció kifejezéseinek szótár-referenciája

ÉN; m. 1. Könyv. Amit meghatároz, azt az határozza meg, amit l. A hang a sebesség meghatározója lehet. Az idő fő meghatározója a Nap mozgása a világűrben. 2. Spec. Útmutató (könyv vagy táblázat) annak meghatározásához, hogy mi ...... enciklopédikus szótár

Könyvek

• A fás szárú növények zárvatermőinek kulcsa gyümölcsökkel és magvakkal, Sinitsyn Jevgenyij Mihajlovics. A determináns két részből áll. Az első rész egy táblázat a nemzetségek azonosítására, a második pedig a fás szárú növények zárvatermő fajainak azonosítására szolgáló táblázatokat tartalmazza ...

· döntő négyzet n-edrendű A mátrixok vagy n-edrendű determináns algebrai összeggel egyenlő számnak nevezzük P! tagjai, amelyek mindegyike egy termék P mátrixelemek minden sorból és oszlopból egyet vettek bizonyos előjelekkel. A determinánst vagy jelöli.

Másodrendű determináns a következőképpen kifejezett szám: . például .

Harmadik rendű determináns a háromszögek szabálya szerint számítva (Sarrus-szabály): .

Példa. .

Megjegyzés. A gyakorlatban a harmadrendű determinánsokat, valamint a magasabb rendűeket a determinánsok tulajdonságai alapján számítják ki.

N-edrendű determinánsok tulajdonságai.

1. A determináns értéke nem változik, ha minden sor (oszlop) helyére egy azonos számú oszlop (sor) kerül - átültetni.

2. Ha a determináns egyik sora (oszlopa) nullákból áll, akkor a determináns értéke nulla.

3. Ha a determinánsban két sort (oszlopot) felcserélünk, akkor a determináns abszolút értéke nem változik, az előjel pedig az ellenkezőjére változik.

4. A két azonos sort (oszlopot) tartalmazó determináns egyenlő nullával.

5. Egy sor (oszlop) összes elemének közös tényezője kivehető a determináns előjeléből.

· Kisebb a determináns valamely eleme P a sorrendet determinánsnak ( P-1)-edik sorrend, amelyet az eredetiből annak a sornak és oszlopnak a törlésével kapunk, amelynek metszéspontjában a kiválasztott elem található. Megnevezés: .

· Algebrai összeadás a determináns elemét minornak nevezzük, a jellel együtt. Megnevezés: Szóval =.

6. A négyzetmátrix determinánsa megegyezik bármely sor (vagy oszlop) elemeinek és algebrai komplementereik szorzatának összegével ( dekompozíciós tétel).

7. Ha a -edik sor minden eleme az összeg k kifejezéseket, akkor a determinánst összegként ábrázoljuk k olyan determinánsok, amelyekben a -edik sor kivételével minden sor megegyezik az eredeti determinánsban szereplővel, és az első determináns -edik sora az első tagokból áll, a másodikban - a második és így tovább. Ugyanez igaz az oszlopokra is.

8. A determináns nem változik, ha az egyik sorhoz (oszlophoz) egy újabb sor (oszlop) szorozva kerül.

Következmény. Ha a többi sorának (oszlopának) lineáris kombinációját hozzáadjuk a determináns sorához (oszlopához), akkor a determináns nem változik.

9. Egy átlós mátrix determinánsa egyenlő a főátlón lévő elemek szorzatával, azaz.

Megjegyzés. A háromszög alakú mátrix determinánsa megegyezik a főátlón lévő elemek szorzatával is.

A determinánsok felsorolt ​​tulajdonságai lehetővé teszik számításuk jelentős egyszerűsítését, ami különösen fontos a magasrendű determinánsoknál. Ilyenkor célszerű az eredeti mátrixot úgy átalakítani, hogy az átalakított mátrixban legyen minél több nullát tartalmazó sor vagy oszlop („nullázás” sorok vagy oszlopok).

Példák. Számítsa ki újra az előző példában megadott determinánst a determinánsok tulajdonságainak felhasználásával!

Döntés: Vegye figyelembe, hogy az első sorban van egy közös tényező - 2, a másodikban pedig egy közös tényező 3, ezeket kivesszük a determináns előjelből (5-ös tulajdonság szerint). Ezután kibővítjük a determinánst, például az első oszlopban, a 6. tulajdonság segítségével (kiterjesztési tétel).

Leghatékonyabb módszer a determináns átlós vagy háromszög alakúra redukálására . Egy mátrix determinánsának kiszámításához elegendő a mátrix olyan transzformációját végrehajtani, amely nem változtatja meg a determinánst, és lehetővé teszi a mátrix átlóssá alakítását.

Végezetül megjegyezzük, hogy ha egy négyzetmátrix determinánsa egyenlő nullával, akkor a mátrixot ún. elfajzott (vagy speciális) , másképp - nem degenerált .

1. A determináns nem változik az átültetés során.

2. Ha a determináns egyik sora nullákból áll, akkor a determináns egyenlő nullával.

3. Ha a determinánsban két sor átrendeződik, a determináns előjelet vált.

4. A két azonos karakterláncot tartalmazó determináns egyenlő nullával.

5. Ha a determináns valamelyik sorának minden elemét megszorozzuk valamilyen k számmal, akkor maga a determináns is megszorozódik k-val.

6. A két arányos sort tartalmazó determináns egyenlő nullával.

7. Ha a determináns i-edik sorának minden elemét két a i j = b j + c j (j= ) tag összegeként adjuk meg, akkor a determináns egyenlő a determinánsok összegével, amelyben minden sor, kivéve az i-edik sorra ugyanazok, mint az adott determinánsban, és az egyik összegző i-edik sora b j elemekből, a másikban c j elemekből áll.

8. A determináns nem változik, ha egy másik sor megfelelő elemeit ugyanazzal a számmal szorozva hozzáadjuk valamelyik sorának elemeihez.

Megjegyzés. Minden tulajdonság érvényben marad, ha sorok helyett oszlopokat vesz fel.

Kisebb Az n-edrendű d determináns a i j elemének M i j-e az n-1 rendű determináns, amelyet d-ből kapunk az ezt az elemet tartalmazó sor és oszlop törlésével.

Algebrai összeadás a d determináns a i j eleme a (-1) i + j jellel felvett moll M i j . Az a i j elem algebrai komplementerét A i j -vel jelöljük. Így A i j = (-1) i + j M i j .

A determinánsok gyakorlati számításának módszereit azon a tényen alapuló, hogy az n-rendű determináns alacsonyabb rendű determinánsokkal is kifejezhető, a következő tétel adja meg.

Tétel (a determináns bontása sorban vagy oszlopban).

A determináns egyenlő tetszőleges sora (vagy oszlopa) összes elemének és algebrai komplementereinek szorzatának összegével. Más szóval, létezik d felosztása az i-edik sor elemei szerint d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = )

vagy j-edik oszlop d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).

Különösen, ha egy sor (vagy oszlop) minden eleme egy kivételével nulla, akkor a determináns egyenlő ennek az elemnek az algebrai komplementerével szorozva.

Példa 1.4. Nem számítjuk ki a determinánst , mutassuk meg, hogy egyenlő nullával. Döntés. Vonjuk ki az első sort a második sorból, megkapjuk a determinánst megegyezik az eredetivel. Ha az első sort is kivonjuk a harmadik sorból, akkor megkapjuk a determinánst , amelyben a két sor arányos. Ez a determináns nulla.

1.5. példa. Számítsuk ki a D = determinánst , kibővítve a második oszlop elemeivel.

Döntés. Bővítsük ki a determinánst a második oszlop elemeivel:

D = a 12 A 12 + a 22 A 22 + a 32 A 32 =

Példa 1.6. Számítsd ki a determinánst

A=
, amelyben a főátló egyik oldalán lévő összes elem nullával egyenlő. Döntés. Bővítsük ki az A determinánst az első sorban: A = a 11 A 11 = . A jobb oldali determináns az első sorban ismét bővíthető, ekkor kapjuk:

A=
.Stb. N lépés után az A = a 11 a 22... a nn egyenlőséghez jutunk.

3.Lineáris egyenletrendszerek alapfogalmai. Cramer tétele.

Meghatározás. Lineáris egyenletrendszer a szakszervezet n lineáris egyenletek, amelyek mindegyike tartalmazza k változók. Így van írva:

Sokan, amikor először találkoznak magasabb algebrával, tévesen azt hiszik, hogy az egyenletek számának szükségszerűen egybe kell esnie a változók számával. Az iskolai algebrában általában ez a helyzet, de a magasabb algebrára ez általában nem igaz.

Meghatározás. Egyenletrendszer megoldása egy számsorozat ( k 1 ,k 2 , ..., k n), amely a rendszer minden egyenletének megoldása, azaz. amikor a változók helyett ebbe az egyenletbe behelyettesítjük x 1 , x 2 , ..., x n helyes számértéket ad meg.

Illetőleg, oldja meg az egyenletrendszert azt jelenti, hogy megtaláljuk az összes megoldásának halmazát, vagy bebizonyítjuk, hogy ez a halmaz üres. Mivel az egyenletek száma és az ismeretlenek száma nem azonos, három eset lehetséges:

1. A rendszer inkonzisztens, i.e. az összes megoldás halmaza üres. Meglehetősen ritka eset, amely könnyen észlelhető, függetlenül attól, hogy melyik módszerrel kell megoldani a rendszert.

2. A rendszer konzisztens és meghatározott, azaz. pontosan egy megoldása van. A klasszikus változat, az iskola óta jól ismert.

3. A rendszer kompatibilis és nincs definiálva, azaz. végtelenül sok megoldása van. Ez a legnehezebb lehetőség. Nem elég kijelenteni, hogy "a rendszernek végtelen számú megoldása van" - le kell írni, hogy ez a halmaz hogyan van elrendezve.

Meghatározás. Változó x i hívott megengedett, ha csak a rendszer egy egyenletében szerepel, és 1-es együtthatóval. Vagyis a többi egyenletben a változó együtthatója x i egyenlőnek kell lennie nullával.

Ha minden egyenletben kiválasztunk egy megengedett változót, akkor a teljes egyenletrendszerre vonatkozó megengedett változók halmazát kapjuk. Magát a rendszert, ebben a formában írva, szintén engedélyezettnek nevezzük. Általánosságban elmondható, hogy egy és ugyanaz a kezdeti rendszer redukálható különböző engedélyezett rendszerekre, de ez most nem érint minket. Példák az engedélyezett rendszerekre:

Mindkét rendszer megengedett a változók tekintetében x 1 , x 3 és x 4. Ugyanilyen sikerrel azonban vitatható, hogy a második rendszer viszonylag megengedett x 1 , x 3 és x 5. Elegendő az utolsó egyenletet átírni így x 5 = x 4 .

Most vegyünk egy általánosabb esetet. Legyen nálunk minden k változók, ebből r megengedett. Ekkor két eset lehetséges:

1. Engedélyezett változók száma r megegyezik a változók teljes számával k: r = k. A rendszert onnan kapjuk k egyenletek, amelyekben r = k megengedett változók. Egy ilyen rendszer együttműködésen alapuló és határozott, mert x 1 = b 1 , x 2 = b 2 , ..., x k = b k;

2. Engedélyezett változók száma r kevesebb, mint a változók teljes száma k: r < k. A maradék ( k − r) a változókat szabadnak nevezzük - bármilyen értéket felvehetnek, amelyből az engedélyezett változók könnyen kiszámíthatók.

Így a fenti rendszerekben a változók x 2 , x 5 , x 6 (az első rendszerhez) és x 2 , x 5 (a második) ingyenes. Azt az esetet, amikor vannak szabad változók, jobb tételként megfogalmazni...

Hogyan kell megoldani?: – Lineáris egyenletrendszer megoldása helyettesítési módszerrel („iskolamódszer”).
– A rendszer megoldása rendszeregyenletek tagonkénti összeadásával (kivonásával).
– A rendszer megoldása Cramer-képletekkel.
– A rendszer megoldása inverz mátrix segítségével.
–A rendszer Gauss módszerrel történő megoldása.

KRAMER

Először nézzük meg a Cramer-szabályt két ismeretlennel rendelkező lineáris egyenletrendszerre. Léteznek kétváltozós lineáris egyenletrendszerek, melyeket célszerű pontosan Cramer-szabály szerint megoldani!

Tekintsük az egyenletrendszert

Első lépésben kiszámítjuk a determinánst, ezt ún a rendszer fő meghatározója.

Ha , akkor a rendszernek végtelen sok megoldása van, vagy inkonzisztens (nincs megoldása). Ebben az esetben a Cramer-szabály nem segít, használni kell Gauss módszer.

Ha , akkor a rendszernek egyedi megoldása van, és a gyökök megtalálásához további két determinánst kell kiszámítanunk: és

A gyakorlatban a fenti minősítőket latin betűvel is jelölhetjük.

Az egyenlet gyökereit a következő képletekkel találjuk meg:,

7. példa

Oldjon meg egy lineáris egyenletrendszert!

Látjuk, hogy az egyenlet együtthatói elég nagyok, a jobb oldalon tizedes törtek vannak vesszővel. A vessző meglehetősen ritka vendég a matematikai gyakorlati feladatokban, ezt a rendszert egy ökonometriai feladatból vettem át.

Hogyan lehet megoldani egy ilyen rendszert? Megpróbálhatja az egyik változót egy másikkal kifejezni, de ebben az esetben minden bizonnyal iszonyatos díszes törteket kap, amelyekkel rendkívül kényelmetlen dolgozni, és a megoldás kialakítása borzasztóan fog kinézni. A második egyenletet megszorozhatja 6-tal, és tagonként kivonhatja, de itt ugyanazok a törtek jelennek meg.

Mit kell tenni? Ilyen esetekben a Cramer-féle képletek segítenek.

A rendszer tehát egyedülálló megoldást kínál.

;

;

Amint láthatja, a gyökerek irracionálisnak bizonyultak, és megközelítőleg megtalálhatók, ami meglehetősen elfogadható (sőt általános) az ökonometriai problémák esetében.

Itt nincs szükség megjegyzésekre, mivel a feladatot kész képletek szerint oldják meg, azonban van egy figyelmeztetés. Ennek a módszernek a használatakor kötelező A feladat töredéke a következő: « , így a rendszer egyedi megoldást kínál . Ellenkező esetben a bíráló megbüntetheti Önt Cramer tételének figyelmen kívül hagyása miatt.

Nem lesz felesleges ellenőrizni, ami kényelmesen elvégezhető egy számológépen: a közelítő értékeket a rendszer minden egyenlete bal oldalán helyettesítjük. Ennek eredményeként kis hibával a jobb oldalon lévő számokat kell megkapni.

Cramer-képletek

Cramer módszere szerint egymás után megtaláljuk fő rendszerazonosító(5.3), azaz mátrix A determináns

és n segédhatározók D i (i= ), amelyeket a D determinánsból kapunk úgy, hogy az i-edik oszlopot szabad tagok oszlopával helyettesítjük.

A Cramer-képletek a következő alakúak:

D × x i = D i (i = ). (5.4)

Az (5.4)-ből Cramer-szabály következik, amely kimerítő választ ad az (5.3) rendszer kompatibilitásának kérdésére: ha a rendszer fő meghatározója nullától eltérő, akkor a rendszernek egyedi megoldása van, amelyet a képletek határoznak meg. :

Ha a D rendszer és az összes D i segéddetermináns fődeterminánsa = 0 (i= ), akkor a rendszernek végtelen számú megoldása van. Ha a rendszer fő determinánsa D = 0, és legalább egy segéddetermináns különbözik nullától, akkor a rendszer inkonzisztens.

1.14. példa. Oldja meg az egyenletrendszert Cramer módszerével:

x 1 + x 2 + x 3 + x 4 = 5, x 1 + 2x 2 - x 3 + 4x 4 = -2, 2x 1 - 3x 2 - x 3 - 5x 4 = -2, 3x 1 + x 2 + 2x3 + 11x4 = 0.

Döntés. Ennek a rendszernek a fő meghatározója D = = -142 ¹ 0, tehát a rendszernek egyedi megoldása van. Számítsuk ki a D determinánsból kapott D i (i= ) segéddeterminánsokat úgy, hogy az x i-ben lévő együtthatókból álló oszlopot egy szabad tagokból álló oszlopra cseréljük: D 1 = = - 142, D 2 = = - 284, D 3 = = - 426,

D4= = 142. Ebből következik, hogy x 1 = D 1 / D = 1, x 2 = D 2 / D = 2, x 3 = D 3 / D = 3, x 4 = D 4 / D = -1, a rendszer megoldása a C =(1, 2, 3, -1) T vektor.

Lineáris egyenletrendszerek alapfogalmai. Gauss módszer.

LÁSD FENT.

Gauss-Jordan módszer(ismeretlenek teljes kiküszöbölésének módszere) - lineáris algebrai egyenletek négyzetes rendszereinek megoldására, mátrix inverzének, vektor koordinátáinak egy adott bázison vagy mátrix rangjának meghatározására szolgáló módszer. A módszer a Gauss-módszer módosítása.

Algoritmus

1. Válassza ki a mátrix első bal oldali oszlopát, amelynek legalább egy nullától eltérő értéke van.

2. Ha ebben az oszlopban a legfelső szám nulla, akkor változtassa meg a mátrix teljes első sorát a mátrix másik sorával, ahol ebben az oszlopban nincs nulla.

3. Az első sor összes eleme a kiválasztott oszlop felső elemével van osztva.

4. A fennmaradó sorokból vonja ki az első sort, megszorozva a megfelelő sor első elemével, hogy minden sor első eleme (az első kivételével) nulla legyen.

6. Az eljárás egyszeri megismétlése után egy felső háromszög alakú mátrixot kapunk

7. Vonja ki az utolsó előtti sorból az utolsó sort, megszorozva a megfelelő együtthatóval úgy, hogy a főátlón csak 1 maradjon az utolsó előtti sorban.

8. Ismételje meg az előző lépést a következő sorokhoz. Ennek eredményeként egy identitásmátrixot és egy szabad vektor helyett egy megoldást kapunk (az összes transzformációt el kell végezni vele).

9. Az inverz mátrix megszerzéséhez az összes műveletet ugyanabban a sorrendben kell alkalmazni az identitásmátrixra.

Gauss módszer

Történelmileg az első, legelterjedtebb módszer a lineáris egyenletrendszerek megoldására a Gauss-módszer, vagyis az ismeretlenek egymást követő kiküszöbölésének módszere. Ennek a módszernek a lényege abban rejlik, hogy az ismeretlenek egymást követő kiküszöbölésével az adott rendszer az adott rendszerrel egyenértékű lépcsőzetes (különösen háromszög alakú) rendszerré alakul. Lineáris egyenletrendszer Gauss-módszerrel történő gyakorlati megoldásában kényelmesebb nem magát az egyenletrendszert, hanem ennek a rendszernek a kiterjesztett mátrixát lépcsőzetes formára redukálni, sorain elemi transzformációkat végrehajtani. A transzformáció során egymás után kapott mátrixokat általában ekvivalenciajellel kötjük össze.

1. példa.13. Oldja meg az egyenletrendszert Gauss-módszerrel: x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0.

Döntés. Ennek a rendszernek a kiterjesztett mátrixát írjuk fel

és hajtsa végre a következő elemi transzformációkat a sorain: a) vonja ki az első sort a második és harmadik sorából, megszorozva 3-mal, illetve 2-vel: ~ ;

b) szorozd meg a harmadik sort (-5)-tel, és add hozzá a másodikat: .

Mindezen átalakítások eredményeként ez a rendszer háromszög alakúra redukálódik: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.

Az utolsó egyenletből azt találjuk, hogy z = -1,3. Ha ezt az értéket behelyettesítjük a második egyenletbe, y = -1,2 kapjuk. Továbbra is az első egyenletből x = - 0,7

A JEGYZETKÖZBŐL:

Gauss módszer

A módszer két részből áll - előre és hátra.

A közvetlen mozgatás az SLE mátrix lépcsőzetes formára való kiterjesztésének viselkedéséből áll, elemi sortranszformációk segítségével. Lépcsőzetes mátrixban minden következő sor elején több nulla van, mint az előzőnek - vagy nulla

Példa:

A mátrixsorok elemi transzformációja a következő:

1) a mátrix egy sorának számainak összeadása valamilyen számmal szorozva a mátrix egyik alsó sorához.

2) Helyenként változtasson két sort

A Gauss-módszer fordított mozgása abból áll, hogy egyes változókat szekvenciálisan fejezünk ki másokkal, az alsó nulla sortól kezdve. Az eredmény egy általános megoldás.

Az előrehúzás után 3 lehetőség van a kiterjesztett mátrix lépcsőzetes típusára:

1) Minden következő sor elején pontosan egy nullával több van, mint az előzőben

Példa:

Soronként felírjuk az egyenletet, és az alsó sortól kezdjük megkeresni a változók értékét.

4X 4 \u003d 8Þ X 4 \u003d 2

Helyettesítse az előző egyenletben

2X 3 -3X 4 \u003d -8 azaz 2X 3 -3 * 2 \u003d -8 vagy 2X 3 \u003d -2, Þ X 3 \u003d -1, helyettesítse X3 és X4 a második sorban stb. Az SLU egyetlen megoldását kapjuk

2) A nem nulla sorok száma kevesebb, mint a változók száma. Ekkor az egyik sor elején legalább 2-vel több nulla van, mint az előzőben, és figyelembe vesszük, hogy a következő nem nulla sor nem olyan alakú (0 ... 0 b), ahol a szám b=0

Például:

3) Az utolsó nem nulla sor alakja (0…0/b), ahol b=0 ellentmondó o=b egyenlőségnek felel meg, tehát a rendszer nem kompatibilis

Az SLE megoldása Gauss módszerrel

2X 1 + 3X 2 + X 3 \u003d 1

4X 1 + 5X 2 + 4X 3 = 7

6X 1 +10X 2 -3X 3 = -10

Összeállítjuk a közvetlen mozgás kiterjesztett mátrixát.

Determinánsok számítása n- sorrend:

A determináns fogalma n- a sorrend

A meghatározó tényezőkről szóló cikk segítségével biztosan megtanulja, hogyan lehet megoldani a következő problémákat:

Oldja meg az egyenletet:

és még sok más, amit a tanárok annyira szeretnek kitalálni.

A mátrix determináns vagy egyszerűen a determináns fontos szerepet játszik a lineáris egyenletrendszerek megoldásában. Általában erre a célra találták ki a determinánsokat. Mivel gyakran mondják, hogy "a mátrix meghatározója", ezért itt is említést teszünk a mátrixokról. Mátrix egy téglalap alakú táblázat, amely olyan számokból áll, amelyeket nem lehet felcserélni. A négyzetes mátrix egy olyan táblázat, amelyben azonos számú sor és oszlop van. Csak négyzetmátrixnak lehet determinánsa.

Könnyen megérthető a determinánsok írásának logikája az alábbi séma szerint. Vegyünk egy két egyenletrendszert két ismeretlennel, amelyeket az iskolából ismersz:

A determinánsban az ismeretlenek együtthatói egymás után íródnak: az első sorban - az első egyenletből, a második sorban - a második egyenletből:

Például, ha adott egy egyenletrendszer

akkor az ismeretlenek együtthatóiból a következő determinánst képezzük:

Tehát tegyük fel, hogy kapunk egy négyzet alakú táblázatot, amely számokból áll n sorok (vízszintes sorok) és be n oszlopok (függőleges sorok). Ezeknek a számoknak a segítségével néhány szabály szerint, amelyeket alább tanulmányozunk, találnak egy számot, amelyet hívnak döntő n sorrendben, és a következőképpen jelöljük:

(1)

A számokat hívják elemeket determináns (1) (az első index a sor számát jelenti, a második - annak az oszlopnak a számát, amelynek metszéspontjában egy elem található; én = 1, 2, ..., n; j= 1, 2, ..., n). Egy determináns sorrendje a sorok és oszlopok száma.

A determináns azon elemeit összekötő képzeletbeli egyenes, amelyre mindkét index azonos, azaz. elemeket

hívott főátló, a másik átló az oldal.

Másod- és harmadrendű determinánsok számítása

Mutassuk meg, hogyan számítjuk ki az első három rend determinánsait.

Az elsőrendű determináns maga az elem, azaz.

A másodrendű determináns a következőképpen kapott szám:

, (2)

Az elemek szorzata a fő- és másodlagos átlón, ill.

A (2) egyenlőség azt mutatja, hogy a főátló elemeinek szorzatát annak előjelével, a másodlagos átló elemeinek szorzatát pedig ellenkező előjellel vesszük. .

1. példa Számítsa ki a másodrendű determinánsokat:

Döntés. A (2) képlet alapján a következőket kapjuk:

A harmadik rendű determináns a következőképpen kapott szám:

(3)

Nehéz megjegyezni ezt a képletet. Van azonban egy egyszerű szabály, az ún háromszög szabály , ami megkönnyíti a kifejezés reprodukálását (3). A determináns elemeit pontokkal jelölve egyenes szakaszokkal kötjük össze közülük azokat, amelyek a determináns elemeinek szorzatát adják (1. ábra).

A (3) képlet azt mutatja, hogy a főátló elemeinek szorzatait, valamint két háromszög csúcsaiban található elemeket, amelyeknek az alapjai párhuzamosak vele, előjelükkel vesszük; ellentétesekkel - a másodlagos átló elemeinek szorzatai, valamint a vele párhuzamos két háromszög csúcsaiban található elemek .

Az 1. ábrán a főátló és a hozzá tartozó háromszögek alapjai, valamint a hozzá tartozó másodlagos átló és a háromszögek alapjai piros színnel vannak kiemelve.

A determinánsok számításánál nagyon fontos, hogy a gimnáziumhoz hasonlóan, ne feledjük, hogy a mínusz szám mínusz számmal szorozva pluszjelet, a plusz jel és mínusz szám szorzata pedig mínusz előjelű számot eredményez.

2. példa Számítsa ki a harmadrendű determinánst:

Döntés. A háromszögek szabályát használva azt kapjuk

Determinánsok számítása n- a sorrend

A determináns sor- vagy oszlopbővítése

A determináns kiszámításához n sorrendben szükséges ismerni és használni a következő tételt.

Laplace-tétel. A determináns egyenlő bármely sor elemeinek és algebrai komplementereik szorzatának összegével, azaz.

Meghatározás. Ha a determinánsban n sorrendben önkényesen válasszon p vonalak és p oszlopok ( p < n), akkor ezeknek a soroknak és oszlopoknak a metszéspontjában lévő elemek sorrendi mátrixot alkotnak.

Ennek a mátrixnak a determinánsát ún kiskorú eredeti meghatározó. Vegyük például a determinánst:

Építsünk mátrixot páros számú sorokból és oszlopokból:

Döntő

hívott kiskorú meghatározó . Másodrendű kiskorút kapott. Nyilvánvaló, hogy különféle első-, másod- és harmadrendű kiskorúak konstruálhatók.

Ha veszünk egy elemet, és kihúzzuk azt a sort és oszlopot, amelynek metszéspontjában a determinánsban áll, akkor egy moll-ot kapunk, amelyet az elem molljának nevezünk, és ezt jelöljük:

.

Ha a moll-ot megszorozzuk -val, ahol 3 + 2 annak a sornak és oszlopnak az összege, amelynek metszéspontjában az elem áll, akkor a kapott szorzatot ún. algebrai összeadás elemet jelöli,

Általánosságban elmondható, hogy egy elem mollját jelöli, az algebrai komplementerét pedig,

(4)

Például számítsuk ki az elemek algebrai komplementereit és a harmadrendű determinánst:

A (4) képlet alapján azt kapjuk

Egy determináns felbontásánál gyakran használjuk a determináns következő tulajdonságát n- sorrend:

ha egy másik sor vagy oszlop megfelelő elemeinek konstans tényezővel való szorzatát hozzáadjuk bármely sor vagy oszlop elemeihez, akkor a determináns értéke nem változik.

4. példa

Előzetesen vonjuk ki a negyedik sor elemeit az első és a harmadik sorból, akkor lesz

A kapott determináns negyedik oszlopában három elem nulla. Ezért jövedelmezőbb ezt a meghatározót a negyedik oszlop elemeivel bővíteni, mivel az első három szorzat nulla lesz. Így

Ezzel ellenőrizheti a megoldást determináns kalkulátor online .

A következő példa pedig bemutatja, hogy bármely (jelen esetben a negyedik) rend determinánsának kiszámítása hogyan redukálható a másodrendű determináns kiszámítására.

5. példa Számítsa ki a determinánst:

Vonjuk ki az első sor elemeit a harmadik sorból, és adjuk hozzá az első sor elemeit a negyedik sor elemeihez, akkor kapunk

Az első oszlopban az első kivételével minden elem nulla. Azaz a determináns már az első oszlopban bontható. De igazán nem akarjuk a harmadrendű determinánst kiszámítani. Ezért további átalakításokat fogunk végezni: a második sor elemeit 2-vel szorozva hozzáadjuk a harmadik sor elemeihez, és kivonjuk a második sor elemeit a negyedik sor elemeiből. Ennek eredményeként a determináns, amely egy algebrai komplementer, maga is kibővíthető az első oszlopban, és csak a másodrendű determinánst kell kiszámítanunk, és nem szabad összekeveredni az előjelekben:

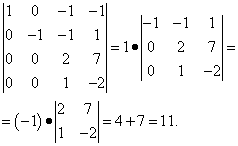
A determináns háromszög formába hozása

Háromszögnek nevezzük azt a determinánst, ahol az egyik átló egyik oldalán lévő összes elem egyenlő nullával. A másodlagos átló esete a főátló esetére redukálódik a sorok vagy oszlopok sorrendjének megfordításával. Egy ilyen determináns egyenlő a főátló elemeinek szorzatával.

A háromszög alakúra redukáláshoz a determináns ugyanazt a tulajdonságát használjuk n sorrendben, amit az előző bekezdésben használtunk: ha bármely sor vagy oszlop elemeihez hozzáadjuk egy másik sor vagy oszlop megfelelő elemeinek szorzatát állandó tényezővel, akkor a determináns értéke nem változik.

Ezzel ellenőrizheti a megoldást determináns kalkulátor online .

Meghatározó tulajdonságok n- a sorrend

Az előző két bekezdésben már használtuk a determináns egyik tulajdonságát n- a sorrend. Egyes esetekben a determináns számításának egyszerűsítése érdekében a determináns egyéb fontos tulajdonságait is felhasználhatja. Például le lehet redukálni egy determinánst két determináns összegére, amelyek közül az egyik vagy mindkettő kényelmesen kiterjeszthető egy sor vagy oszlop mentén. Rengeteg eset van ilyen leegyszerűsítésre, és a determináns egyik vagy másik tulajdonságának felhasználását egyénileg kell eldönteni.

Mátrix meghatározó (mátrix meghatározó) egy négyzet alakú számok vagy matematikai szimbólumok táblázata ( Δd).

Meghatározás. mátrix meghatározó n×n ez a szám:

ahol ( α 1, α 2,...,α n) - számok permutációja innen 1 előtt n, N (α 1 , α 2 ,..., α n)- az inverziók száma a permutációban, az összegzés a sorrend összes lehetséges permutációján megtörténik n.

Mátrix meghatározó A alapvetően ún de t(A), |A|, vagy ?(A).

Paraméterek, amelyek segítségével minden típusú algebrai mátrix megoldása megtalálható.

Nak nek mátrix determináns keresése mátrix megoldásánál ismerni kell a mátrixok alapvető tulajdonságait és a műveletsorokat.

1. A sorrendi mátrixokhoz n=2 a determinánst a következő képlet segítségével találjuk meg: Δ= a11*egy 22-egy 12*a 21
2. A sorrendi mátrixokhoz n=3 a determinánst algebrai összeadásokkal vagy a Sarrus-módszerrel találjuk meg.
3. A >3 dimenziójú mátrixot algebrai összeadásokra bontjuk, amelyekhez megtaláljuk a determinánsaikat (minorokat). Például egy 4. rendű mátrix determinánsát a sorok vagy oszlopok kibontásával számítják ki.

Mert mátrix determináns megtalálása, amely függvényeket tartalmaz a mátrixban, szabványos módszereket használunk. Például egy harmadik rendű mátrix determinánsának megkereséséhez:

Használjuk az első sor bővítményét:

Δ = sin(x) × + 1× = 2sin(x) cos(x) - 2cos(x) = sin(2x) - 2cos(x)

Számítsa ki a mátrix determinánsát!

Számítsa ki a mátrix determinánst Számos módszer létezik, amelyeket alább felsorolunk.

A mátrix determinánsának kiszámításának legnépszerűbb módja az algebrai összeadások kiválasztásának módszere. Ennek a módszernek van egy egyszerűbb változata - a determináns kiszámítása a Sarrus-szabály segítségével. Ezek a módszerek különböznek egy egyszerű kis mátrix determinánsának kiszámításakor, és ha nagy dimenziójú mátrixot kell kiszámítani, akkor ilyen mátrix determináns számítási módszerek:

• a determináns kiszámítása rendeléscsökkentési módszerrel,
• a determináns kiszámítása Gauss-módszerrel (a mátrix háromszög alakúra redukálásával),
• a determináns kiszámítása dekompozíciós módszerrel.

Az Excelben a determináns kiszámításához a = MOPRED (cellatartomány) függvényt használjuk.