DETERMINANTE
o determinante, - in matematica, registrando i numeri sotto forma di tavola quadrata, in corrispondenza della quale viene posto un altro numero (il “valore” del determinante). Molto spesso, il concetto di "determinante" indica sia il significato del determinante che la forma della sua registrazione. I determinanti consentono di scrivere comodamente espressioni complesse che si presentano, ad esempio, quando si risolvono equazioni lineari nella geometria analitica e nell'analisi matematica. La scoperta dei determinanti è attribuita al matematico giapponese S. Kova (1683) e, indipendentemente, a G. Leibniz (1693). La teoria moderna risale ai lavori di J. Binet, O. Cauchy e C. Jacobi dell'inizio del XIX secolo. Il determinante più semplice è formato da 4 numeri, detti elementi, disposti su 2 righe e 2 colonne. Tale determinante si dice di 2° ordine. Ad esempio, questo è il determinante

Il cui valore è 2*5 - 3*1 (ovvero 10 - 3 o 7). Nel caso generale, il determinante del 2° ordine è solitamente scritto nella forma

E il suo valore è uguale a a1b2 - a2b1, dove aeb sono numeri o funzioni. Il determinante del 3° ordine è formato da 9 elementi disposti su 3 righe e 3 colonne. In generale, il determinante dell'ordine n è costituito da n2 elementi e solitamente viene scritto come

Il primo indice di ciascun elemento indica il numero della riga, il secondo il numero della colonna all'intersezione della quale si trova questo elemento, quindi aij è un elemento i-esima riga e jesima colonna. Spesso tale determinante viene scritto come |aij|. Un metodo per calcolare il determinante, quasi sempre utilizzato quando si calcolano determinanti di ordine superiore, è l'espansione "minore". Un minore corrispondente a qualsiasi elemento di un determinante è un determinante di 1 ordine più piccolo, ottenuto dall'originale eliminando la riga e la colonna all'intersezione delle quali si trova questo elemento.

Il “complemento algebrico” di un elemento è il suo minore, preso con segno più se la somma dei numeri di riga e colonna alla cui intersezione sta l'elemento è pari, e con segno meno se è dispari. Nell'esempio sopra, l'elemento a2 è nella prima colonna e nella seconda riga; la somma (1+2) è dispari, e quindi il complemento algebrico dell'elemento a2 è uguale al suo minore preso con segno meno, cioè

Il valore del determinante è uguale alla somma dei prodotti degli elementi di qualsiasi riga (o qualsiasi colonna) per i loro complementi algebrici. Ad esempio, il determinante

espanso lungo la prima colonna, ha la forma

e la sua espansione lungo la seconda linea ha la forma

Calcolando ciascun minore e moltiplicandolo per un coefficiente, è facile verificare che entrambe le espressioni coincidono. Valore determinante. Sotto il valore del determinante

È consuetudine intendere la somma di tutti i prodotti di n elementi, cioè

In questa formula si sommano tutte le permutazioni j1, ј, jn dei numeri 1, 2, ј, n e si antepone al termine il segno più se la permutazione è pari e il segno meno se questa è la permutazione è strana. Questa somma ammonta esattamente a n! termini, metà dei quali sono presi con il segno più, metà con il segno meno. Ciascun termine della somma contiene un termine da ciascuna colonna e ciascuna riga del determinante. Si può dimostrare che questa somma coincide con l'espressione ottenuta espandendo il determinante nei minori.
Proprietà del determinante. Tra le proprietà più importanti del determinante ricordiamo le seguenti. (i) Se tutti gli elementi di qualsiasi riga (o qualsiasi colonna) sono zero, allora il valore del determinante è zero:

(ii) Se gli elementi di due righe (o due colonne) sono uguali o proporzionali, allora il valore del determinante è zero:

(iii) Il valore del determinante non cambierà se tutte le sue righe e colonne vengono scambiate, cioè scrivi la prima riga come prima colonna, la seconda riga come seconda colonna, ecc. (questa operazione si chiama trasposizione). Per esempio,

(iv) Il valore del determinante non cambierà se agli elementi di una riga (o colonna) vengono aggiunti gli elementi corrispondenti di un'altra riga (o colonna), moltiplicati per un fattore arbitrario. L'esempio seguente moltiplica gli elementi della seconda riga per -2 e li aggiunge agli elementi della prima riga:

(v) Se due righe (o due colonne) vengono scambiate, il determinante cambierà segno:

(vi) Se tutti gli elementi di una riga (o di una colonna) contengono un fattore comune, allora questo fattore può essere tolto dal segno determinante:

Esempio. Calcoliamo il valore del seguente determinante del 4° ordine:

Aggiungiamo la quarta riga alla prima riga:

Sottrai la prima colonna dalla quarta colonna:

Moltiplica la terza colonna per 3 e sottrai dalla quarta colonna:

Se lo si desidera, le righe e le colonne possono essere scambiate:

Espandiamo il determinante negli elementi della quarta riga. Tre elementi di questa riga sono zero, l'elemento diverso da zero è nella terza colonna e poiché la somma (3 + 4) è dispari, il suo complemento algebrico ha un segno meno. Di conseguenza otteniamo:

Il minore può essere espanso negli elementi della terza riga: due dei suoi elementi sono uguali a zero, e un elemento diverso da zero è nella terza colonna; la somma (3 + 3) è pari, quindi l'uguaglianza precedente può essere continuata:

Applicazioni. Risoluzione di un sistema di equazioni

può essere ottenuto moltiplicando la prima equazione per b2, la seconda per b1, e poi sottraendo un'equazione dall'altra. Dopo aver eseguito queste operazioni, otteniamo

O se

Quello

Questa notazione della soluzione mediante determinanti può essere generalizzata al caso di risoluzione di un sistema di n equazioni lineari con n incognite; ogni determinante sarà dell'ennesimo ordine. Il determinante di un sistema di equazioni lineari

Volere

Si noti che se D = 0, le equazioni sono incoerenti o non indipendenti. Pertanto, il calcolo preliminare del determinante D consente di verificare se il sistema di equazioni lineari è risolvibile.
Determinanti in geometria analitica. L'equazione generale di una sezione conica può essere rappresentata come

Determinante

è chiamato discriminante. Se D = 0, allora la curva degenera in una coppia di rette parallele o intersecanti oppure in un punto (vedi anche SEZIONI CONICHE). Un altro esempio: l'area di un triangolo A con vertici nei punti (trasversale - antiorario) (x1, y1), (x2, y2) e (x3, y3) è data da

Relazione tra determinanti e matrici. Una matrice è la registrazione di una serie di numeri sotto forma di tabella rettangolare. I determinanti sono associati a matrici quadrate; ad esempio, determinante della matrice

Se A, B e C sono matrici quadrate allora |A|*|B| = |C|.
Vedi anche ALGEBRA ASTRATTA.
Jacobiano. Se x = f (u, v), y = g (u, v) è una trasformazione di coordinate, allora il determinante

Si chiama Jacobiano o determinante Jacobiano di questa trasformazione. Se J non è uguale a 0 in un punto, allora nelle sue vicinanze le equazioni di trasformazione possono essere risolte in modo univoco rispetto a u e v, rappresentandole come funzioni di x e y.
Vedi ANALISI MATEMATICA.

Enciclopedia di Collier. - Società aperta. 2000 .

Sinonimi:

Scopri cosa significa "QUALIFICANTE" in altri dizionari:

DETERMINANTE, determinante, marito. (libro). 1. Ciò che definisce, esprime qualcosa. 2. Un libro utilizzato come riferimento per determinare qualcosa (scientifico). Chiave della pianta. Chiave a fungo. 3. Espressione composta da... ... Dizionario esplicativo di Ushakov

- (determinante) un'espressione matematica compilata secondo una determinata regola da n2 numeri, utilizzata per risolvere e studiare sistemi di equazioni algebriche di 1o grado. Il numero n è chiamato ordine del determinante. Quindi, un determinante del 2° ordine... Grande dizionario enciclopedico

Identificatore, dell'Assia, minore, determinante Dizionario dei sinonimi russi. sostantivo determinante, numero di sinonimi: 10 determinante automatico (1) ... Dizionario dei sinonimi

DETERMINANTE- (determinante) un'espressione matematica composta secondo una certa regola da n2 numeri, utilizzata per risolvere e studiare sistemi di equazioni algebriche di 1o grado. Il numero n è chiamato ordine del determinante. Quindi, un determinante del 2° ordine... Grande Enciclopedia del Politecnico

DETERMINANTE, io, marito. 1. Un dispositivo per determinare cosa n., e anche, in generale, con l'aiuto del quale si può fare cosa n. determinare con precisione, stabilire. Telefono con ID chiamante. O. ritmo. 2. Un libro di riferimento per determinare cosa. (specialista.). O. piante... Dizionario esplicativo di Ozhegov

- (determinante della) matrice quadrata A = ||aij|| ordine n, detA polinomio... Enciclopedia fisica

determinante- - Argomenti delle telecomunicazioni, concetti base EN determinante... Guida del traduttore tecnico

Questo termine ha altri significati, vedi Determinante (significati). Determinante (o determinante) è uno dei concetti di base dell'algebra lineare. Il determinante di una matrice è un polinomio degli elementi di una matrice quadrata (cioè uno... Wikipedia

determinante- 3.4.6 ausiliari: codice classe ausiliari UDC. Fonte … Dizionario-libro di consultazione dei termini della documentazione normativa e tecnica

IO; 1. Libro. Ciò che è determinato da ciò che è determinato. Il suono può essere un determinante della velocità. Il principale fattore determinante del tempo è il movimento del Sole nello spazio. 2. Speciale Una guida (libro o tabella) per determinare cosa... ... Dizionario enciclopedico

Libri

• Chiave per le piante legnose angiosperme da frutti e semi, Sinitsyn Evgeniy Mikhailovich. Il determinante è composto da due parti. La prima parte è una tabella per l'identificazione dei generi, la seconda comprende tabelle per l'identificazione delle specie di piante legnose angiosperme in base...

· Determinante piazza matrici A di ordine n O determinante dell'ennesimo ordine è un numero uguale a una somma algebrica N! membri, ognuno dei quali è un prodotto N elementi della matrice presi uno da ogni riga e da ogni colonna con determinati segni. Il determinante è indicato con o.

Determinante del secondo ordineè un numero espresso come segue: . Per esempio .

Determinante del terzo ordine calcolato utilizzando la regola del triangolo (regola di Sarrus): .

Esempio. .

Commento. In pratica, i determinanti del terzo ordine, così come quelli di ordine superiore, vengono calcolati utilizzando le proprietà dei determinanti.

Proprietà dei determinanti di ordine ennesimo.

1. Il valore del determinante non cambierà se ogni riga (colonna) viene sostituita da una colonna (riga) con lo stesso numero - trasporre.

2. Se una delle righe (colonne) del determinante è composta da zero, il valore del determinante è zero.

3. Se due righe (colonne) vengono scambiate nel determinante, il valore assoluto del determinante non cambierà, ma il segno cambierà al contrario.

4. Un determinante contenente due righe (colonne) identiche è uguale a zero.

5. Il fattore comune di tutti gli elementi di una riga (colonna) può essere portato oltre il segno del determinante.

· Minore qualche elemento del determinante N-esimo ordine è chiamato determinante ( N-1)esimo ordine, ottenuto dall'originale barrando la riga e la colonna all'intersezione delle quali si trova l'elemento selezionato. Designazione: .

· Complemento algebrico l'elemento del determinante si chiama minore, preso con il segno. Designazione: T.o. =.

6. Il determinante di una matrice quadrata è uguale alla somma dei prodotti degli elementi di qualsiasi riga (o colonna) per i loro complementi algebrici ( teorema di decomposizione).

7. Se ogni elemento della -esima riga rappresenta una somma k termini, allora il determinante è rappresentato come una somma k determinanti in cui tutte le linee tranne la -esima linea sono le stesse del determinante originale, e la -esima linea nel primo determinante consiste dei primi termini, nella seconda - del secondo, ecc. Lo stesso vale per le colonne.

8. Il determinante non cambierà se un'altra riga (colonna) viene aggiunta a una delle righe (colonne), moltiplicata per il numero.

Conseguenza. Se una combinazione lineare delle sue altre righe (colonne) viene aggiunta a una riga (colonna) di un determinante, il determinante non cambierà.

9. Il determinante di una matrice diagonale è uguale al prodotto degli elementi sulla diagonale principale, cioè

Commento. Anche il determinante di una matrice triangolare è uguale al prodotto degli elementi sulla diagonale principale.

Le proprietà elencate dei determinanti consentono di semplificare significativamente il loro calcolo, il che è particolarmente importante per i determinanti di ordine elevato. In questo caso è consigliabile trasformare la matrice originale in modo che la matrice trasformata abbia una riga o colonna contenente il maggior numero possibile di zeri (righe o colonne “azzerate”).

Esempi. Calcoliamo nuovamente il determinante indicato nell'esempio precedente, utilizzando le proprietà dei determinanti.

Soluzione: Nota che nella prima riga c'è un fattore comune - 2, e nella seconda - un fattore comune 3, li togliamo dal segno determinante (per la proprietà 5). Successivamente, espandiamo il determinante, ad esempio, nella prima colonna, utilizzando la proprietà 6 (il teorema di espansione).

Più efficace metodo per ridurre il determinante alla forma diagonale o triangolare . Per calcolare il determinante di una matrice è sufficiente eseguire una trasformazione della matrice che non cambia il determinante e permette di trasformare la matrice in una diagonale.

In conclusione, notiamo che se il determinante di una matrice quadrata è uguale a zero, allora la matrice viene chiamata degenerare (o speciale) , Altrimenti - non degenerato .

1. Il determinante non cambia durante la trasposizione.

2. Se una delle linee del determinante è composta da zeri, allora il determinante è uguale a zero.

3. Se due righe del determinante vengono riorganizzate, il determinante cambierà segno.

4. Un determinante contenente due stringhe identiche è uguale a zero.

5. Se tutti gli elementi di una determinata riga del determinante vengono moltiplicati per un numero k, il determinante stesso verrà moltiplicato per k.

6. Un determinante contenente due linee proporzionali è uguale a zero.

7. Se tutti gli elementi della i-esima riga del determinante sono presentati come la somma di due termini a i j = b j + c j (j= ), allora il determinante è uguale alla somma dei determinanti per cui tutte le righe, tranne la i -esimo, sono gli stessi del determinante dato, A i-esima riga in uno dei termini è costituito da elementi b j, nell'altro da elementi c j.

8. Il determinante non cambia se agli elementi di una delle sue righe si sommano gli elementi corrispondenti di un'altra riga, moltiplicati per lo stesso numero.

Commento. Tutte le proprietà rimangono valide se prendiamo colonne invece di righe.

Minore M i j dell'elemento a i j del determinante d dell'ordine n è detto determinante di ordine n-1, che si ottiene da d eliminando la riga e la colonna contenente questo elemento.

Complemento algebrico l'elemento a i j del determinante d si chiama suo minore M i j , preso con il segno (-1) i + j . Il complemento algebrico di un elemento a i j sarà denotato con A i j . Pertanto, A i j = (-1) i + j M i j .

Il metodo pratico per il calcolo dei determinanti, basato sul fatto che un determinante di ordine n può essere espresso in termini di determinanti di ordine inferiore, è dato dal seguente teorema.

Teorema (scomposizione del determinante in una riga o colonna).

Il determinante è uguale alla somma dei prodotti di tutti gli elementi della sua riga (o colonna) arbitraria per i loro complementi algebrici. In altre parole, c’è un’espansione di d in elementi dell'i-esimo linee d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = )

oppure la jesima colonna d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).

In particolare, se tutti gli elementi tranne uno di una riga (o colonna) sono zero, allora il determinante è uguale a quell'elemento moltiplicato per il suo complemento algebrico.

Esempio 1.4. Senza calcolare il determinante , dimostra che è uguale a zero. Soluzione. Sottrai la prima riga dalla seconda riga e ottieni il determinante , uguale a quello originale. Se sottraiamo anche la prima dalla terza riga, otteniamo il determinante , in cui le due righe sono proporzionali. Questo determinante è uguale a zero.

Esempio 1.5. Calcolare il determinante D = , scomponendolo negli elementi della seconda colonna.

Soluzione. Espandiamo il determinante negli elementi della seconda colonna:

D = a 12 A 12 + a 22 A 22 + a 32 A 32 =

Esempio 1.6. Determinante del calcolo

A=
, in cui tutti gli elementi su un lato della diagonale principale sono uguali a zero. Soluzione. Espandiamo il determinante di A lungo la prima riga: A = a 11 A 11 = . Il determinante a destra può essere espanso nuovamente lungo la prima riga, quindi otteniamo:

A=
.E così via. Dopo n passi arriviamo all'uguaglianza A = a 11 a 22... a nn.

3.Concetti di base sui sistemi di equazioni lineari. Il teorema di Cramer.

Definizione. Sistema di equazioni lineariè un'unione di N equazioni lineari, ciascuna delle quali contiene k variabili. E' scritto così:

Molti, quando incontrano per la prima volta l'algebra superiore, credono erroneamente che il numero di equazioni debba necessariamente coincidere con il numero di variabili. Nell'algebra scolastica questo di solito accade, ma per l'algebra superiore generalmente non è vero.

Definizione. Risoluzione di un sistema di equazioniè una sequenza di numeri ( k 1 ,k 2 , ..., k n), che è la soluzione di ciascuna equazione del sistema, cioè quando si sostituisce in questa equazione invece delle variabili X 1 , X 2 , ..., x n fornisce l'uguaglianza numerica corretta.

Rispettivamente, risolvere il sistema di equazioni- significa trovare l'insieme di tutte le sue soluzioni o dimostrare che questo insieme è vuoto. Poiché il numero di equazioni e il numero di incognite potrebbero non coincidere, sono possibili tre casi:

1. Il sistema è incoerente, vale a dire l'insieme di tutte le soluzioni è vuoto. Questo è un caso abbastanza raro che viene facilmente rilevato indipendentemente dal metodo utilizzato per risolvere il sistema.

2. Il sistema è coerente e definito, vale a dire ha esattamente una soluzione. La versione classica, conosciuta fin dai tempi della scuola.

3. Il sistema è coerente e indefinito, vale a dire ha infinite soluzioni. Questa è l'opzione più difficile. Non è sufficiente indicare che “il sistema ha un insieme infinito di soluzioni” – è necessario descrivere come è strutturato questo insieme.

Definizione. Variabile x io chiamato consentito, se è compreso in una sola equazione del sistema, e con coefficiente pari a 1. In altre parole, nelle restanti equazioni il coefficiente della variabile x io deve essere uguale a zero.

Se selezioniamo una variabile consentita in ciascuna equazione, otteniamo un insieme di variabili consentite per l'intero sistema di equazioni. Anche il sistema stesso, scritto in questa forma, si dirà risolto. In generale, uno stesso sistema originario può essere ridotto a diversi consentiti, ma per ora questo non ci preoccupa. Ecco alcuni esempi di sistemi consentiti:

Entrambi i sistemi sono risolti in modo variabile X 1 , X 3 e X 4. Tuttavia, con lo stesso successo si può sostenere che il secondo sistema è relativamente consentito X 1 , X 3 e X 5. È sufficiente riscrivere l'ultima equazione nella forma X 5 = X 4 .

Consideriamo ora un caso più generale. Possiamo avere tutto k variabili, di cui R sono ammessi. Allora sono possibili due casi:

1. Numero di variabili consentite R pari al numero totale di variabili k: R = k. Otteniamo il sistema da k equazioni in cui R = k variabili consentite. Un tale sistema è congiunto e definito, perché X 1 = B 1 , X 2 = B 2 , ..., xk = b k;

2. Numero di variabili consentite R meno numero totale variabili k: R < k. Il riposo ( k − R) le variabili sono chiamate libere: possono assumere qualsiasi valore, da cui è possibile calcolare facilmente le variabili consentite.

Quindi, nei sistemi di cui sopra le variabili X 2 , X 5 , X 6 (per il primo sistema) e X 2 , X 5 (per il secondo) sono gratuiti. Il caso in cui ci sono variabili libere è meglio formulato come teorema...

Come risolvere?: – Risoluzione di un sistema di equazioni lineari utilizzando il metodo delle sostituzioni (“metodo scolastico”).
– Risolvere il sistema mediante addizione (sottrazione) termine per termine delle equazioni del sistema.
–Soluzione del sistema utilizzando le formule di Cramer.
–Risolvere il sistema utilizzando una matrice inversa.
–Risoluzione del sistema utilizzando il metodo gaussiano.

KRAMER

Consideriamo innanzitutto la regola di Cramer per un sistema di due equazioni lineari in due incognite. Esistono sistemi di equazioni lineari a due variabili che è consigliabile risolvere utilizzando la regola di Cramer!

Consideriamo il sistema di equazioni

Nel primo passaggio calcoliamo il determinante, si chiama determinante principale del sistema.

Se , allora il sistema ha infinite soluzioni oppure è incoerente (non ha soluzioni). In questo caso, la regola di Cramer non aiuta, è necessario utilizzarla Metodo gaussiano.

Se , allora il sistema ha un'unica soluzione, e per trovare le radici dobbiamo calcolare altri due determinanti: e

In pratica, le qualificazioni di cui sopra possono anche essere denotate da una lettera latina.

Troviamo le radici dell'equazione usando le formule:

Esempio 7

Risolvere un sistema di equazioni lineari

Vediamo che i coefficienti dell'equazione sono piuttosto grandi; sul lato destro ci sono le frazioni decimali con una virgola. La virgola è un ospite piuttosto raro nei compiti pratici di matematica; ho preso questo sistema da un problema econometrico.

Come risolvere un sistema del genere? Puoi provare a esprimere una variabile in termini di un'altra, ma in questo caso probabilmente ti ritroverai con frazioni terribili e fantasiose con cui è estremamente scomodo lavorare, e il design della soluzione sembrerà semplicemente terribile. Puoi moltiplicare la seconda equazione per 6 e sottrarre termine per termine, ma anche qui si presenteranno le stesse frazioni.

Cosa fare? In questi casi, le formule di Cramer vengono in soccorso.

Ciò significa che il sistema ha una soluzione unica.

;

;

Come puoi vedere, le radici si sono rivelate irrazionali e sono state trovate approssimativamente, il che è abbastanza accettabile (e persino banale) per i problemi di econometria.

I commenti non sono necessari qui, poiché il compito viene risolto utilizzando formule già pronte, tuttavia, c'è un avvertimento. Quando si utilizza questo metodo, obbligatorio Un frammento della progettazione dell'attività è il seguente frammento: « , il che significa che il sistema ha una soluzione unica" . Altrimenti, il revisore potrebbe punirti per mancanza di rispetto per il teorema di Cramer.

Non sarebbe superfluo il controllo, che può essere comodamente effettuato su una calcolatrice: sostituiamo valori approssimati nella parte sinistra di ciascuna equazione del sistema. Di conseguenza, con un piccolo errore, dovresti ottenere i numeri che si trovano sul lato destro.

Le formule di Cramer

Il metodo di Cramer è che troviamo costantemente determinante principale del sistema(5.3), cioè determinante della matrice A

E n determinanti ausiliari D i (i= ), che si ottengono dal determinante D sostituendo la colonna i-esima con una colonna di termini liberi.

Le formule di Cramer assomigliano a:

D × x io = D io (i = ). (5.4)

Dalla (5.4) segue la regola di Cramer, che fornisce una risposta esaustiva alla questione della compatibilità del sistema (5.3): se il determinante principale del sistema è diverso da zero, allora il sistema ha un'unica soluzione, determinata dalle formule:

Se il determinante principale del sistema D e tutti i determinanti ausiliari D i = 0 (i= ), allora il sistema ha un numero infinito di soluzioni. Se il determinante principale del sistema D = 0, e almeno un determinante ausiliario è diverso da zero, allora il sistema è incoerente.

Esempio 1.14. Risolvi il sistema di equazioni utilizzando il metodo Cramer:

x 1 + x 2 + x 3 + x 4 = 5, x 1 + 2x 2 - x 3 + 4x 4 = -2, 2x 1 - 3x 2 - x 3 - 5x 4 = -2, 3x 1 + x 2 + 2x3 + 11x4 = 0.

Soluzione. Il principale determinante di questo sistema è D = = -142 ¹ 0, il che significa che il sistema ha una soluzione unica. Calcoliamo i determinanti ausiliari D i (i= ), ottenuti dal determinante D sostituendo in esso la colonna costituita dai coefficienti di x i con una colonna di termini liberi: D 1 = = - 142, D2 = = - 284, D3 = = - 426,

D4= = 142. Quindi x 1 = D 1 /D = 1, x 2 = D 2 /D = 2, x 3 = D 3 /D = 3, x 4 = D 4 /D = -1, la soluzione del sistema è il vettore C =(1, 2, 3, -1) T .

Concetti di base sui sistemi di equazioni lineari. Metodo gaussiano.

VEDI SOPRA.

Metodo di Gauss-Jordan(metodo di eliminazione completa delle incognite) - un metodo utilizzato per risolvere sistemi quadratici di equazioni algebriche lineari, trovare l'inverso di una matrice, trovare le coordinate di un vettore in una determinata base o trovare il rango di una matrice. Il metodo è una modifica del metodo di Gauss.

Algoritmo

1. Seleziona la prima colonna della matrice da sinistra, che contiene almeno un valore diverso da zero.

2. Se il numero più in alto in questa colonna è zero, scambia l'intera prima riga della matrice con un'altra riga della matrice in cui non c'è zero in questa colonna.

3. Tutti gli elementi della prima riga vengono divisi per l'elemento superiore della colonna selezionata.

4. Dalle restanti righe, sottrarre la prima riga, moltiplicata per il primo elemento della riga corrispondente, in modo da ottenere zero come primo elemento di ciascuna riga (eccetto la prima).

6. Dopo aver ripetuto questa procedura una volta, si ottiene la matrice triangolare superiore

7. Sottrarre dalla penultima riga l'ultima riga, moltiplicata per il coefficiente corrispondente, in modo che nella penultima riga rimanga solo 1 sulla diagonale principale.

8. Ripetere il passaggio precedente per le righe successive. Di conseguenza, otteniamo una matrice identità e una soluzione al posto del vettore libero (è necessario eseguire con esso le stesse trasformazioni).

9. Per ottenere la matrice inversa, è necessario applicare tutte le operazioni nello stesso ordine alla matrice identità.

Metodo di Gauss

Storicamente, il primo metodo più comune per risolvere sistemi di equazioni lineari è il metodo di Gauss, o il metodo di eliminazione sequenziale delle incognite. L'essenza di questo metodo è quella attraverso la successiva eliminazione delle incognite questo sistema si trasforma in un sistema graduale (in particolare triangolare) equivalente a questo. Quando si risolve praticamente un sistema di equazioni lineari utilizzando il metodo gaussiano, è più conveniente ridurre a una forma graduale non il sistema di equazioni stesso, ma la matrice estesa di questo sistema, eseguendo trasformazioni elementari sulle sue righe. Le matrici sequenziali ottenute durante la trasformazione sono solitamente collegate da un segno di equivalenza.

Esempio 1.13. Risolvi il sistema di equazioni utilizzando il metodo di Gauss: x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0.

Soluzione. Scriviamo la matrice estesa di questo sistema

ed eseguire sulle sue linee le seguenti trasformazioni elementari: a) dalla sua seconda e terza linea sottrarre la prima, moltiplicata rispettivamente per 3 e 2: ~ ;

b) moltiplicare la terza riga per (-5) e aggiungervi la seconda: .

Come risultato di tutte queste trasformazioni, questo sistema si riduce alla forma triangolare: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.

Dall'ultima equazione troviamo z = -1,3. Sostituendo questo valore nella seconda equazione, abbiamo y = -1,2. Successivamente, dalla prima equazione otteniamo x = - 0,7

DAL TACCUINO:

Metodo di Gauss

Il metodo è composto da due parti: avanti e indietro.

L'approccio diretto consiste nell'espandere la matrice SLN in una forma a scaglioni utilizzando trasformazioni di riga elementari. In una matrice a gradini, ogni riga successiva ha più zeri iniziali della precedente oppure è zero

Esempio:

Le trasformazioni di riga della matrice elementare sono:

1) sommando i numeri di una riga della matrice, moltiplicati per un numero, a una delle righe inferiori della matrice.

2) Scambia due righe

Il contrario del metodo gaussiano consiste nell'esprimere sequenzialmente alcune variabili in termini di altre, a partire dalla linea dello zero inferiore. Il risultato è una soluzione generale.

Dopo un tratto diretto sono possibili 3 opzioni per la forma a gradini della matrice estesa:

1) Ogni riga successiva ha esattamente uno zero in più all'inizio rispetto alla precedente

Esempio:

Scriviamo l'equazione riga per riga e iniziamo a trovare i valori delle variabili dalla riga inferiore.

4Þ 4 =8Þ å 4 =2

Sostituisci nell'equazione precedente

2X 3 -3X 4 = -8 cioè 2X 3 -3 * 2=-8 oppure 2X 3 =-2, Þ X 3 =-1, sostituisci X3 e X4 nella seconda riga, ecc. Otteniamo l'unica soluzione per SLU

2) Il numero di righe diverse da zero è inferiore al numero di variabili. Allora una delle righe contiene all'inizio almeno 2 zeri in più della precedente e assumiamo che la riga successiva diversa da zero non abbia la forma (0...0 b) dove il numero b=0

Per esempio:

3) L'ultima riga diversa da zero ha la forma (0...0/b), dove b=0 corrisponde alle uguaglianze contraddittorie o=b, quindi il sistema è incompatibile

Risoluzione degli SLE utilizzando il metodo gaussiano

2X1 +3X2 +X3 =1

4X1 +5X2 +4X3 =7

6X1 +10X2 -3X3 = -10

Componiamo una matrice di movimento in avanti estesa.

Calcolo dei determinanti N-esimo ordine:

Il concetto di determinante N-esimo ordine

Usando questo articolo sui determinanti, imparerai sicuramente come risolvere problemi come i seguenti:

Risolvi l'equazione:

e molti altri che gli insegnanti adorano inventare.

Il determinante di una matrice, o semplicemente il determinante, gioca un ruolo importante nella risoluzione di sistemi di equazioni lineari. In generale, i determinanti sono stati inventati a questo scopo. Poiché spesso si dice anche “determinante di una matrice”, qui menzioneremo anche le matrici. Matriceè una tabella rettangolare composta da numeri che non possono essere scambiati. Una matrice quadrata è una tabella che ha lo stesso numero di righe e colonne. Solo una matrice quadrata può avere un determinante.

È facile comprendere la logica della registrazione dei determinanti utilizzando il seguente schema. Prendiamo un sistema di due equazioni in due incognite, che ti è familiare a scuola:

Nel determinante, i coefficienti per le incognite sono scritti in sequenza: nella prima riga - dalla prima equazione, nella seconda riga - dalla seconda equazione:

Ad esempio, se dato un sistema di equazioni

allora dai coefficienti delle incognite si forma il seguente determinante:

Quindi, diamo una tabella quadrata composta da numeri disposti in N linee (file orizzontali) e in N colonne (righe verticali). Utilizzando questi numeri, secondo alcune regole che studieremo di seguito, trovano il numero che chiamano determinante N-esimo ordine e indicato come segue:

(1)

I numeri vengono chiamati elementi determinante (1) (il primo indice indica il numero della riga, il secondo il numero della colonna all'intersezione della quale si trova l'elemento; io = 1, 2, ..., N; J= 1, 2, ..., n). L'ordine di un determinante è il numero delle sue righe e colonne.

Una linea retta immaginaria che collega gli elementi del determinante per il quale entrambi gli indici sono gli stessi, cioè elementi

chiamato diagonale principale, un'altra diagonale – lato.

Calcolo dei determinanti del secondo e del terzo ordine

Mostriamo come vengono calcolate le determinanti dei primi tre ordini.

Il determinante del primo ordine è l'elemento stesso, cioè

Il determinante del secondo ordine è il numero ottenuto come segue:

, (2)

Il prodotto degli elementi situati rispettivamente sulla diagonale principale e secondaria.

L'uguaglianza (2) mostra che il prodotto degli elementi della diagonale principale è preso con il proprio segno, e il prodotto degli elementi della diagonale secondaria con il segno opposto .

Esempio 1. Calcolare i determinanti del secondo ordine:

Soluzione. Usando la formula (2) troviamo:

Un determinante del terzo ordine è un numero ottenuto come segue:

(3)

È difficile ricordare questa formula. Tuttavia, esiste una semplice regola chiamata regola del triangolo , il che rende facile riprodurre l'espressione (3). Denotando gli elementi del determinante con punti, colleghiamo con segmenti di linea retta quelli che danno il prodotto degli elementi del determinante (Fig. 1).

La formula (3) mostra che i prodotti degli elementi della diagonale principale, nonché gli elementi situati ai vertici di due triangoli le cui basi sono parallele ad essa, sono presi con i loro segni; con quelli opposti: il prodotto degli elementi della diagonale laterale, nonché degli elementi situati ai vertici di due triangoli paralleli ad essa .

Nella Fig. 1 sono evidenziate in rosso la diagonale principale e le basi corrispondenti dei triangoli e la diagonale secondaria e le basi corrispondenti dei triangoli.

Quando si calcolano i determinanti, è molto importante, come alle scuole superiori, ricordare che un numero con segno meno moltiplicato per un numero con segno meno dà come risultato un numero con segno più, e un numero con segno più moltiplicato per a numero con segno meno restituisce un numero con segno meno.

Esempio 2. Calcolare il determinante del terzo ordine:

Soluzione. Utilizzando la regola del triangolo otteniamo

Calcolo dei determinanti N-esimo ordine

Espansione del determinante per riga o colonna

Per calcolare il determinante N-esimo ordine, è necessario conoscere e utilizzare il seguente teorema.

Il teorema di Laplace. Il determinante è uguale alla somma dei prodotti degli elementi di qualsiasi riga e dei loro complementi algebrici, cioè

Definizione. Se nel determinante N ordine: scegli arbitrariamente P linee e P colonne ( P < N), quindi gli elementi situati all'intersezione di queste righe e colonne formano una matrice d'ordine.

Il determinante di questa matrice si chiama minore il determinante originario. Consideriamo ad esempio il determinante:

Costruiamo una matrice da righe e colonne con numeri pari:

Determinante

chiamato minore determinante Abbiamo un minore del secondo ordine. È chiaro che da ciò si possono costruire diversi minori del primo, secondo e terzo ordine.

Se prendiamo un elemento e cancelliamo la riga e la colonna nel determinante alla cui intersezione si trova, otteniamo un minore chiamato elemento minore, che denotiamo con:

.

Se il minore viene moltiplicato per , dove 3 + 2 è la somma dei numeri di riga e colonna all'intersezione dei quali si trova un elemento, il prodotto risultante viene chiamato complemento algebrico elemento ed è indicato con

In generale, indicheremo il minore di un elemento, e il complemento algebrico,

(4)

Ad esempio, calcoliamo i complementi algebrici degli elementi e del determinante del terzo ordine:

Usando la formula (4) otteniamo

Quando si decompone un determinante, viene spesso utilizzata la seguente proprietà del determinante N-esimo ordine:

Se il prodotto degli elementi corrispondenti di un'altra riga o colonna viene sommato agli elementi di una riga o colonna con un fattore costante, il valore del determinante non cambierà.

Esempio 4.

Per prima cosa sottraiamo gli elementi della quarta riga dalla prima e dalla terza riga, quindi avremo

La quarta colonna del determinante risultante contiene tre elementi: zeri. Pertanto, è più vantaggioso espandere questo determinante negli elementi della quarta colonna, poiché i primi tre prodotti saranno zero. Ecco perché

Puoi controllare la soluzione utilizzando calcolatore determinante online .

E l'esempio seguente mostra come il calcolo di un determinante di qualsiasi ordine (in questo caso del quarto ordine) possa essere ridotto al calcolo di un determinante del secondo ordine.

Esempio 5. Calcola il determinante:

Sottraiamo gli elementi della prima riga dalla terza riga, e aggiungiamo gli elementi della prima riga agli elementi della quarta riga, quindi avremo

Nella prima colonna tutti gli elementi tranne il primo sono zero. Cioè, il determinante può già essere espanso sulla prima colonna. Ma in realtà non vogliamo calcolare il determinante del terzo ordine. Effettueremo quindi alcune ulteriori trasformazioni: agli elementi della terza riga aggiungeremo gli elementi della seconda riga, moltiplicati per 2, e dagli elementi della quarta riga sottrarremo gli elementi della seconda riga. Di conseguenza, il determinante, che è un complemento algebrico, può essere sviluppato esso stesso lungo la prima colonna e dovremo solo calcolare il determinante del secondo ordine e non confonderci nei segni:

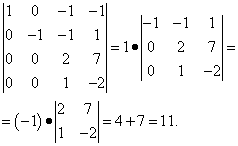
Riduzione del determinante alla forma triangolare

Un determinante in cui tutti gli elementi che giacciono su un lato di una delle diagonali sono uguali a zero si dice triangolare. Invertendo l'ordine delle righe o delle colonne, il caso di una diagonale secondaria si riduce al caso della diagonale principale. Questo determinante è uguale al prodotto degli elementi della diagonale principale.

Per ridurre alla forma triangolare si utilizza la stessa proprietà del determinante N-esimo ordine, che abbiamo applicato nel paragrafo precedente: se il prodotto degli elementi corrispondenti di un'altra riga o colonna per un fattore costante viene aggiunto agli elementi di una riga o colonna, il valore del determinante non cambierà.

Puoi controllare la soluzione utilizzando calcolatore determinante online .

Proprietà del determinante N-esimo ordine

Nei due paragrafi precedenti abbiamo già utilizzato una delle proprietà del determinante N-esimo ordine. In alcuni casi, per semplificare il calcolo del determinante, è possibile utilizzare altre importanti proprietà del determinante. Ad esempio, è possibile ridurre un determinante alla somma di due determinanti, uno o entrambi dei quali possono essere opportunamente espansi in qualche riga o colonna. Esistono molti casi di tale semplificazione e la questione dell'utilizzo dell'una o dell'altra proprietà del determinante dovrebbe essere risolta individualmente.

Determinante della matrice (determinante della matrice) è una tabella quadrata di numeri o simboli matematici ( Δd).

Definizione. Determinante della matrice n×nè il numero:

Dove ( α 1 , α 2 ,...,α n) - permutazione di numeri da 1 A N, N (α 1 ,α 2 ,...,α n)- numero di inversioni in una permutazione, la somma avviene su tutte le possibili permutazioni dell'ordine N.

Determinante della matrice UN generalmente indicato come de t(A), |A|, O ?(UN).

Parametri utilizzati per trovare soluzioni a tutti i tipi di matrici algebriche.

A trovare il determinante della matriceè necessario conoscere le proprietà di base delle matrici e la sequenza delle azioni quando si risolve una matrice.

1. Per matrici d'ordine n=2 il determinante si trova utilizzando la formula: Δ= un 11*un 22 -un 12*un 21
2. Per matrici d'ordine n=3 il determinante si trova mediante addizioni algebriche o utilizzando il metodo Sarrus.
3. Una matrice con dimensione >3 viene scomposta in complementi algebrici, per i quali si trovano i propri determinanti (minori). Ad esempio, il determinante di una matrice del 4° ordine viene calcolato tramite espansione di riga o di colonna.

Per trovare il determinante della matrice, che contiene funzioni nella matrice, vengono utilizzati metodi standard. Ad esempio, trova il determinante di una matrice del terzo ordine:

Usiamo l'espansione lungo la prima riga:

Δ = sin(x) × + 1× = 2sen(x) cos(x) - 2cos(x) = sin(2x) - 2cos(x)

Calcolare il determinante della matrice.

Calcolare il determinante di una matrice possibile utilizzando diversi metodi, che verranno elencati di seguito.

Il modo più diffuso per calcolare il determinante di una matrice è il metodo di selezione dei complementi algebrici. Esiste una versione più semplice di questo metodo: calcolare il determinante utilizzando la regola di Sarrus. Questi metodi sono eccellenti quando si calcola il determinante di una matrice semplice piccola e se è necessario calcolare una matrice ad alta dimensione, è possibile utilizzare quanto segue metodi per calcolare il determinante di una matrice:

• calcolo del determinante utilizzando il metodo di riduzione dell'ordine,
• calcolo del determinante utilizzando il metodo gaussiano (riducendo la matrice alla forma triangolare),
• calcolo del determinante mediante il metodo della scomposizione.

In Excel, la funzione =MOPRED(intervallo di celle) viene utilizzata per calcolare il determinante.