DETERMINANT
sau determinant, - la matematică, înregistrarea numerelor sub formă de tabel pătrat, în conformitate cu care se pune un alt număr („valoarea” determinantului). De foarte multe ori, termenul „determinant” înseamnă atât sensul determinantului, cât și forma notației acestuia. Determinanții fac posibilă scrierea convenabilă a expresiilor complexe care apar, de exemplu, la rezolvarea ecuațiilor liniare în geometria analitică și în analiza matematică. Descoperirea determinanților este atribuită matematicianului japonez S. Kova (1683) și, independent, lui G. Leibniz (1693). Teoria modernă se întoarce la lucrările lui J. Binet, O. Cauchy și C. Jacobi la începutul secolului al XIX-lea. Cel mai simplu determinant este format din 4 numere, numite elemente, dispuse pe 2 rânduri și 2 coloane. Se spune că un astfel de determinant este de ordinul 2. De exemplu, acesta este determinantul

A cărui valoare este 2*5 - 3*1 (adică 10 - 3 sau 7). În cazul general, determinantul de ordinul 2 se scrie de obicei sub forma

Și valoarea sa este a1b2 - a2b1, unde a și b sunt numere sau funcții. Determinantul de ordinul 3 este format din 9 elemente dispuse pe 3 rânduri și 3 coloane. În general, determinantul de ordinul al n-lea constă din n2 elemente și este de obicei scris ca

Primul index al fiecărui element indică numărul rândului, al doilea - numărul coloanei la intersecția căreia se află acest element, deci aij este elementul rândului i și al coloanei j. Adesea un astfel de determinant este scris ca |aij|. Una dintre metodele de calcul a determinantului, folosită aproape întotdeauna în calculul determinanților de ordin superior, este extinderea în „minori”. Un minor corespunzător oricărui element al determinantului este un determinant de ordin mai mic decât 1, obținut din cel original prin ștergerea rândului și coloanei la intersecția cărora se află acest element. De exemplu, minorul corespunzător elementului a2 din determinant

„Complementul algebric” al unui element este minorul acestuia, luat cu semnul plus dacă suma numerelor de rând și coloane la intersecția cărora se află elementul este pară și cu semnul minus dacă este impar. În exemplul de mai sus, elementul a2 se află în prima coloană și în al 2-lea rând; suma (1 + 2) este impară și, prin urmare, complementul algebric al elementului a2 este egal cu minorul său, luat cu semnul minus, i.e.

Valoarea determinantului este egală cu suma produselor elementelor oricărui rând (sau oricărei coloane) și a complementelor lor algebrice. De exemplu, determinantul

extins peste prima coloană are forma

iar extinderea sa în al doilea rând are forma

Calculând fiecare minor și înmulțindu-l cu un coeficient, este ușor de verificat că ambele expresii sunt aceleași. Valoarea determinantului. Sub valoarea determinantului

Se obișnuiește să se înțeleagă suma tuturor produselor a n elemente, adică.

În această formulă, însumarea se realizează peste toate permutările j1, ј, jn ale numerelor 1, 2, ј, n, iar termenul este precedat de un semn plus dacă permutarea este pară și de un semn minus dacă această permutare este impară. . O astfel de sumă totalizează exact n! membri, dintre care jumătate sunt luate cu semnul plus, jumătate - cu semnul minus. Fiecare termen sumă conține câte un termen din fiecare coloană și fiecare rând al determinantului. Se poate dovedi că această sumă coincide cu expresia obţinută prin extinderea determinantului la minori.
Proprietăți determinante. Dintre cele mai importante proprietăți ale determinantului amintim următoarele. (i) Dacă toate elementele oricărui rând (sau oricărei coloane) sunt zero, atunci valoarea determinantului este, de asemenea, zero:

(ii) Dacă elementele a două rânduri (sau două coloane) sunt egale sau proporționale, atunci valoarea determinantului este zero:

(iii) Valoarea determinantului nu se modifică dacă toate rândurile și coloanele sale sunt interschimbate, i.e. scrieți prima linie ca prima coloană, a doua linie ca a doua coloană și așa mai departe. (această operație se numește transpunere). De exemplu,

(iv) Valoarea determinantului nu se modifică dacă la elementele unui rând (sau coloană) adăugăm elementele corespunzătoare ale altui rând (sau coloană) înmulțite cu un factor arbitrar. Următorul exemplu înmulțește elementele celui de-al doilea rând cu -2 și le adaugă la elementele primului rând:

(v) Dacă două rânduri (sau două coloane) sunt schimbate, determinantul își schimbă semnul:

(vi) Dacă toate elementele unui rând (sau unei coloane) conțin un factor comun, atunci acest factor poate fi scos din semnul determinantului:

Exemplu. Calculați valoarea următorului determinant de ordinul 4:

Să adăugăm a 4-a linie la prima linie:

Scădeți prima coloană din a 4-a coloană:

Înmulțiți a treia coloană cu 3 și scădeți din a patra coloană:

Puteți schimba rândurile și coloanele dacă doriți:

Să extindem determinantul cu elementele celui de-al patrulea rând. Trei elemente din acest rând sunt egale cu zero, elementul diferit de zero se află în a treia coloană și, deoarece suma (3 + 4) este impară, complementul său algebric are semnul minus. Ca rezultat, obținem:

Minorul poate fi descompus în elementele celui de-al treilea rând: două dintre elementele sale sunt egale cu zero, iar un element diferit de zero se află în a treia coloană; suma (3 + 3) este pară, deci egalitatea anterioară poate fi continuată:

Aplicații. Rezolvarea unui sistem de ecuații

se poate obține prin înmulțirea primei ecuații cu b2, a doua cu b1 și apoi scăzând o ecuație din cealaltă. Făcând aceste operațiuni, obținem

Sau daca

apoi

O astfel de înregistrare a soluției cu ajutorul determinanților permite generalizarea în cazul rezolvării unui sistem de n ecuații liniare cu n necunoscute; fiecare determinant va fi de ordinul al n-lea. Determinant al unui sistem de ecuații liniare

voi

Rețineți că dacă D = 0, atunci ecuațiile sunt fie inconsistente, fie nu sunt independente. Prin urmare, calculul preliminar al determinantului D vă permite să verificați dacă sistemul de ecuații liniare este rezolvabil.
Determinanți în geometria analitică. Ecuația generală a unei secțiuni conice poate fi reprezentată ca

Determinant

se numeste discriminant. Dacă D = 0, atunci curba degenerează într-o pereche de drepte paralele sau care se intersectează sau într-un punct (vezi și SECȚIUNI CONICE). Un alt exemplu: aria triunghiului A cu vârfuri în puncte (bypass - în sens invers acelor de ceasornic) (x1, y1), (x2, y2) și (x3, y3) este dată de

Legătura determinanților cu matrice. O matrice este o înregistrare a unei matrice de numere sub forma unui tabel dreptunghiular. Determinanții sunt legați de matrice pătrată; de exemplu, determinant de matrice

Dacă A, B și С sunt matrici pătrate și atunci |A|*|B| = |C|.
Vezi si ALGEBRA ESTE ABSTRACTA.
iacobian. Dacă x = f (u, v), y = g (u, v) este o transformare de coordonate, atunci determinantul

Se numește determinantul jacobian sau jacobi al acestei transformări. Dacă J nu este egal cu 0 la un moment dat, atunci în vecinătatea lui ecuațiile de transformare pot fi rezolvate unic în raport cu u și v, reprezentându-le ca funcții ale lui x și y.
Vezi ANALIZA MATEMATICĂ.

Enciclopedia Collier. - Societate deschisă. 2000 .

Sinonime:

Vedeți ce este „DETERMINANT” în alte dicționare:

DETERMINATOR, determinant, masculin. (carte). 1. Ceea ce determină, exprimă ceva. 2. O carte care servește drept referință în determinarea a ceva (științific). Identificarea plantelor. Ghid de ciuperci. 3. O expresie formată din ...... Dicționar explicativ al lui Ushakov

- (determinant) o expresie matematică întocmită după o anumită regulă din n2 numere, utilizată în rezolvarea și studierea sistemelor de ecuații algebrice de gradul I. Numărul n se numește ordinea determinantului. Deci, determinantul de ordinul al 2-lea ... Dicţionar enciclopedic mare

Identificator, hessian, minor, determinant Dicționar de sinonime rusești. determinant substantiv, număr de sinonime: 10 autodeterminator (1) … Dicţionar de sinonime

DETERMINANT- (determinant) o expresie matematică întocmită după o anumită regulă din n2 numere, utilizată în rezolvarea și studierea sistemelor de ecuații algebrice de gradul I. Numărul n se numește ordinea determinantului. Deci, determinantul de ordinul al 2-lea ... Marea Enciclopedie Politehnică

DETERMINER, eu, soț. 1. Un dispozitiv pentru a determina ce n., precum și în general, cu ajutorul căruia este posibil să n. determina exact. Telefon cu ID apelant. O. ritm. 2. O carte de referință atunci când se stabilește ce n. (specialist.). O. plante... Dicționar explicativ al lui Ozhegov

- (determinant) al matricei pătrate A = ||aij|| ordine n, detA polinom... Enciclopedia fizică

determinant- - Subiecte de telecomunicații, concepte de bază EN determinant ... Manualul Traducătorului Tehnic

Acest termen are alte semnificații, vezi Determinant (sensuri). Determinantul (sau determinantul) este unul dintre conceptele de bază ale algebrei liniare. Determinantul matricei este un polinom în elementele unei matrice pătrate (adică astfel încât y ... Wikipedia

determinant- 3.4.6 calificativ (auxiliar): codul clasei auxiliare UDC. O sursă … Dicționar-carte de referință de termeni ai documentației normative și tehnice

eu; m. 1. Carte. Ceea ce este determinat, este determinat de ceea ce l. Sunetul poate fi un factor determinant al vitezei. Principalul determinant al timpului este mișcarea Soarelui în spațiul cosmic. 2. Spec. Un ghid (carte sau tabel) pentru a determina ce ...... Dicţionar enciclopedic

Cărți

• Cheia angiospermelor plantelor lemnoase prin fructe și semințe, Sinitsyn Evgeny Mikhailovici. Determinantul este format din două părți. Prima parte este un tabel pentru identificarea genurilor, iar a doua include tabele pentru identificarea speciilor de angiosperme de plante lemnoase prin ...

· determinant pătrat matricele A de ordinul al n-lea sau determinant de ordinul al n-lea numit număr egal cu suma algebrică P! membri, fiecare dintre acestea fiind un produs P elemente de matrice luate câte unul din fiecare rând și fiecare coloană cu anumite semne. Determinantul se notează prin sau .

Determinant de ordinul doi este un număr exprimat după cum urmează: . De exemplu .

Determinant de ordinul trei calculat după regula triunghiurilor (regula Sarrus): .

Exemplu. .

cometariu. În practică, determinanții de ordinul trei, precum și ordinele superioare, sunt calculate folosind proprietățile determinanților.

Proprietățile determinanților de ordin al n-lea.

1. Valoarea determinantului nu se va modifica dacă fiecare rând (coloană) este înlocuit cu o coloană (rând) cu același număr - transpune.

2. Dacă unul dintre rândurile (coloana) determinantului este format din zerouri, atunci valoarea determinantului este zero.

3. Dacă două rânduri (coloane) sunt interschimbate în determinant, atunci valoarea absolută a determinantului nu se va schimba, iar semnul se va schimba la opus.

4. Determinantul care conține două rânduri (coloane) identice este egal cu zero.

5. Factorul comun al tuturor elementelor unui rând (coloană) poate fi scos din semnul determinantului.

· Minor vreun element al determinantului P Ordinea se numește determinant ( P-1)-a ordine, obținută din original prin ștergerea rândului și coloanei la intersecția cărora se află elementul selectat. Denumire: .

· Adunarea algebrică elementul determinantului se numește minorul său, luat cu semnul . Denumire: Deci =.

6. Determinantul unei matrice pătrate este egal cu suma produselor elementelor oricărui rând (sau coloane) și a complementelor lor algebrice ( teorema de descompunere).

7. Dacă fiecare element al --lea rând este suma k termeni, atunci determinantul este reprezentat ca o sumă k determinanți în care toate rândurile, cu excepția rândului --lea, sunt aceleași ca în determinantul inițial, iar --lea rând din primul determinant este format din primii termeni, în al doilea - din al doilea și așa mai departe. Același lucru este valabil și pentru coloane.

8. Determinantul nu se va modifica dacă la unul dintre rânduri (coloane) se adaugă un alt rând (coloană) înmulțit cu un număr.

Consecinţă. Dacă o combinație liniară a celorlalte rânduri (coloane) este adăugată la rândul (coloana) determinantului, atunci determinantul nu se va modifica.

9. Determinantul unei matrici diagonale este egal cu produsul elementelor de pe diagonala principală, adică.

cometariu. Determinantul unei matrice triunghiulare este, de asemenea, egal cu produsul elementelor de pe diagonala principală.

Proprietățile enumerate ale determinanților fac posibilă simplificarea semnificativă a calculului acestora, ceea ce este deosebit de important pentru determinanții de ordin înalt. În acest caz, este recomandabil să transformați matricea inițială în așa fel încât matricea transformată să aibă un rând sau o coloană care să conțină cât mai multe zerouri (rânduri sau coloane „de zero”).

Exemple. Calculați din nou determinantul dat în exemplul anterior, folosind proprietățile determinanților.

Soluţie: Rețineți că în prima linie există un factor comun - 2, iar în a doua - un factor comun 3, le vom scoate din semnul determinant (prin proprietatea 5). În continuare, extindem determinantul, de exemplu, în prima coloană, folosind proprietatea 6 (teorema expansiunii).

Cel mai eficient metodă de reducere a unui determinant la o formă diagonală sau triunghiulară . Pentru a calcula determinantul unei matrice este suficientă efectuarea unei transformări a matricei care să nu modifice determinantul și să facă posibilă transformarea matricei într-una diagonală.

În concluzie, observăm că dacă determinantul unei matrice pătrate este egal cu zero, atunci matricea se numește degenerat (sau special) , in caz contrar - nedegenerat .

1. Determinantul nu se modifică în timpul transpunerii.

2. Dacă unul dintre rândurile determinantului este format din zerouri, atunci determinantul este egal cu zero.

3. Dacă două rânduri sunt rearanjate în determinant, determinantul își va schimba semnul.

4. Determinantul care conține două șiruri identice este egal cu zero.

5. Dacă toate elementele unui rând al determinantului sunt înmulțite cu un număr k, atunci determinantul însuși va fi înmulțit cu k.

6. Determinantul care conține două rânduri proporționale este egal cu zero.

7. Dacă toate elementele rândului i al determinantului sunt prezentate ca sumă a doi termeni aij = bj + cj (j= ), atunci determinantul este egal cu suma determinanților, în care toate rândurile, cu excepția pentru i-lea rând, sunt aceleași ca în determinantul dat , iar i-lea rând dintr-unul dintre sume este format din elemente bj , în celălalt - din elemente cj .

8. Determinantul nu se modifică dacă elementele corespunzătoare unui alt rând, înmulțite cu același număr, se adaugă elementelor unuia dintre rândurile sale.

Cometariu. Toate proprietățile rămân valabile dacă sunt luate coloane în loc de rânduri.

Minor M i j al elementului a i j al determinantului d de ordinul al n-lea este determinantul de ordinul n-1, care se obține din d prin ștergerea rândului și coloanei care conțin acest element.

Adunarea algebrică elementul a i j al determinantului d este minorul său M i j , luat cu semnul (-1) i + j . Complementul algebric al elementului a i j va fi notat cu A i j . Astfel, A i j = (-1) i + j M i j .

Metodele de calcul practic al determinanților bazate pe faptul că determinantul de ordin n poate fi exprimat în termeni de determinanți de ordin inferior sunt date de următoarea teoremă.

Teorema (descompunerea determinantului într-un rând sau coloană).

Determinantul este egal cu suma produselor tuturor elementelor rândului său (sau coloanei) arbitrare și a complementelor lor algebrice. Cu alte cuvinte, există o descompunere a lui d în ceea ce privește elementele rândului i d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = )

sau j-a coloană d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).

În special, dacă toate elementele unui rând (sau coloană), cu excepția unuia, sunt egale cu zero, atunci determinantul este egal cu acest element înmulțit cu complementul său algebric.

Exemplul 1.4. Nu se calculează determinantul , arătați că este egal cu zero. Soluţie. Scădeți primul rând din al doilea rând, obținem determinantul egal cu originalul. Dacă scădem și primul rând din al treilea rând, obținem determinantul , în care cele două rânduri sunt proporționale. Acest determinant este zero.

Exemplul 1.5. Calculați determinantul D = , extinzându-l cu elementele coloanei a doua.

Soluţie. Să extindem determinantul cu elementele coloanei a doua:

D = a 12 A 12 + a 22 A 22 + a 32 A 32 =

Exemplul 1.6. Calculați determinant

A=
, în care toate elementele de pe o parte a diagonalei principale sunt egale cu zero. Soluţie. Să extindem determinantul A din primul rând: A = a 11 A 11 = . Determinantul din dreapta poate fi extins din nou de-a lungul primei linii, apoi obținem:

A=
.Etc. După n pași, ajungem la egalitatea A = a 11 a 22... a nn.

3.Concepte de bază ale sistemelor de ecuații liniare. teorema lui Cramer.

Definiție. Sistem de ecuații liniare este uniunea de n ecuații liniare, fiecare dintre ele conține k variabile. Este scris astfel:

Mulți, când se confruntă pentru prima dată cu algebra superioară, cred în mod eronat că numărul de ecuații trebuie să coincidă în mod necesar cu numărul de variabile. În algebra școlară, acesta este de obicei cazul, dar pentru algebra superioară acest lucru nu este, în general, adevărat.

Definiție. Rezolvarea unui sistem de ecuații este o succesiune de numere ( k 1 ,k 2 , ..., k n), care este o soluție pentru fiecare ecuație a sistemului, adică când se substituie în această ecuație în loc de variabile X 1 , X 2 , ..., x n dă valoarea numerică corectă.

Respectiv, rezolva sistemul de ecuatiiînseamnă a găsi mulțimea tuturor soluțiilor sale sau a demonstra că această mulțime este goală. Deoarece numărul de ecuații și numărul de necunoscute pot să nu fie același, sunt posibile trei cazuri:

1. Sistemul este inconsecvent, adică setul tuturor soluțiilor este gol. Un caz destul de rar care este ușor de detectat indiferent de metoda de rezolvare a sistemului.

2. Sistemul este consistent și definit, adică are exact o solutie. Varianta clasică, cunoscută încă de la școală.

3. Sistemul este compatibil și nu este definit, adică are infinit de solutii. Aceasta este cea mai grea varianta. Nu este suficient să afirmăm că „sistemul are un set infinit de soluții” - este necesar să descriem modul în care este aranjat acest set.

Definiție. Variabil x i numit permis, dacă este inclus într-o singură ecuație a sistemului, și cu un coeficient de 1. Cu alte cuvinte, în ecuațiile rămase, coeficientul variabilei x i ar trebui să fie egal cu zero.

Dacă selectăm o variabilă permisă în fiecare ecuație, obținem un set de variabile permise pentru întregul sistem de ecuații. Sistemul în sine, scris în această formă, va fi numit și permis. În general, unul și același sistem inițial poate fi redus la diferite sisteme permise, dar acest lucru nu ne privește acum. Iată exemple de sisteme permise:

Ambele sisteme sunt permise cu privire la variabile X 1 , X 3 și X 4 . Totuși, cu același succes se poate argumenta că cel de-al doilea sistem este permis relativ X 1 , X 3 și X cinci . Este suficient să rescrieți ultima ecuație ca X 5 = X 4 .

Acum luați în considerare un caz mai general. Să avem totul k variabile, dintre care r sunt permise. Atunci sunt posibile două cazuri:

1. Numărul de variabile permise r este egal cu numărul total de variabile k: r = k. Primim sistemul de la k ecuaţii în care r = k variabile permise. Un astfel de sistem este colaborativ și definit, pentru că X 1 = b 1 , X 2 = b 2 , ..., x k = b k;

2. Numărul de variabile permise r mai mic decât numărul total de variabile k: r < k. Restul ( k − r) variabilele sunt numite libere - pot lua orice valoare din care variabilele permise sunt ușor de calculat.

Astfel, în sistemele de mai sus, variabilele X 2 , X 5 , X 6 (pentru primul sistem) și X 2 , X 5 (pentru al doilea) sunt gratuite. Cazul în care există variabile libere este mai bine formulat ca o teoremă...

Cum să rezolve?: – Rezolvarea unui sistem de ecuații liniare folosind metoda substituției („metoda școlii”).
– Rezolvarea sistemului prin adunarea (scăderea) termen cu termen a ecuațiilor sistemului.
– Rezolvarea sistemului prin formulele lui Cramer.
– Rezolvarea sistemului folosind matricea inversă.
– Rezolvarea sistemului prin metoda Gauss.

KRAMER

În primul rând, luați în considerare regula lui Cramer pentru un sistem de două ecuații liniare cu două necunoscute. Există sisteme de ecuații liniare cu două variabile, pe care este indicat să le rezolvi exact după regula lui Cramer!

Luați în considerare sistemul de ecuații

La primul pas, calculăm determinantul , se numește principalul determinant al sistemului.

Dacă , atunci sistemul are infinit de soluții sau este inconsecvent (nu are soluții). În acest caz, regula lui Cramer nu va ajuta, trebuie să utilizați metoda Gauss.

Dacă , atunci sistemul are o soluție unică, iar pentru a găsi rădăcinile trebuie să calculăm încă doi determinanți: și

În practică, calificativele de mai sus pot fi notate și prin litera latină.

Rădăcinile ecuației se găsesc prin formulele:,

Exemplul 7

Rezolvați un sistem de ecuații liniare

Vedem că coeficienții ecuației sunt destul de mari, în partea dreaptă sunt fracții zecimale cu virgulă. Virgula este un invitat destul de rar în sarcinile practice la matematică; am luat acest sistem dintr-o problemă econometrică.

Cum se rezolvă un astfel de sistem? Puteți încerca să exprimați o variabilă în termenii alteia, dar, în acest caz, veți obține cu siguranță fracții fanteziste teribile, cu care sunt extrem de incomod de lucrat, iar designul soluției va arăta doar îngrozitor. Puteți înmulți a doua ecuație cu 6 și scădeți termen cu termen, dar aceleași fracții vor apărea aici.

Ce sa fac? În astfel de cazuri, formulele lui Cramer vin în ajutor.

Deci sistemul are o soluție unică.

;

;

După cum puteți vedea, rădăcinile s-au dovedit a fi iraționale și au fost găsite aproximativ, ceea ce este destul de acceptabil (și chiar banal) pentru problemele de econometrie.

Nu sunt necesare comentarii aici, deoarece sarcina este rezolvată conform formulelor gata făcute, totuși, există o avertizare. Când utilizați această metodă, obligatoriu Fragmentul sarcinii este următorul fragment: « , astfel încât sistemul are o soluție unică . În caz contrar, recenzentul vă poate pedepsi pentru nerespectarea teoremei lui Cramer.

Nu va fi de prisos să verificați, ceea ce este convenabil de efectuat cu un calculator: înlocuim valorile aproximative în partea stângă a fiecărei ecuații a sistemului. Ca rezultat, cu o mică eroare, ar trebui să se obțină numerele care sunt în partea dreaptă.

formulele lui Cramer

Metoda lui Cramer este aceea că găsim succesiv identificatorul principal al sistemului(5.3), adică matricea A determinant

Și n determinanţi auxiliari Di (i= ), care se obțin din determinantul D prin înlocuirea coloanei i-a cu o coloană de termeni liberi.

Formulele lui Cramer au forma:

D × x i = D i (i = ). (5,4)

Din (5.4), urmează regula lui Cramer, care dă un răspuns exhaustiv la întrebarea de compatibilitate a sistemului (5.3): dacă principalul determinant al sistemului este diferit de zero, atunci sistemul are o soluție unică, determinată de formulele:

Dacă determinantul principal al sistemului D și toți determinanții auxiliari D i = 0 (i= ), atunci sistemul are un număr infinit de soluții. Dacă determinantul principal al sistemului D = 0 și cel puțin un determinant auxiliar este diferit de zero, atunci sistemul este inconsecvent.

Exemplul 1.14. Rezolvați sistemul de ecuații folosind metoda lui Cramer:

x 1 + x 2 + x 3 + x 4 = 5, x 1 + 2x 2 - x 3 + 4x 4 = -2, 2x 1 - 3x 2 - x 3 - 5x 4 = -2, 3x 1 + x 2 + 2x3 + 11x4 = 0.

Soluţie. Principalul determinant al acestui sistem D = = -142 ¹ 0, deci sistemul are o soluție unică. Să calculăm determinanții auxiliari D i (i= ) obținuți din determinantul D prin înlocuirea în acesta a unei coloane formată din coeficienți la x i cu o coloană de membri liberi: D 1 = = - 142, D 2 = = - 284, D 3 = = - 426,

D4= = 142. Prin urmare, x 1 = D 1 / D = 1, x 2 = D 2 / D = 2, x 3 = D 3 / D = 3, x 4 = D 4 / D = -1, soluția sistemului este vectorul C =(1, 2, 3, -1) T .

Concepte de bază ale sistemelor de ecuații liniare. metoda Gauss.

VEZI DEASUPRA.

metoda Gauss-Jordan(metoda eliminării complete a necunoscutelor) - o metodă care este utilizată pentru a rezolva sisteme pătrate de ecuații algebrice liniare, pentru a găsi inversul unei matrici, pentru a găsi coordonatele unui vector într-o bază dată sau pentru a găsi rangul unei matrice. Metoda este o modificare a metodei Gauss.

Algoritm

1. Selectați prima coloană din stânga a matricei, care are cel puțin o valoare diferită de zero.

2. Dacă numărul cel mai de sus din această coloană este zero, atunci schimbați întregul prim rând al matricei cu un alt rând al matricei, unde nu există zero în această coloană.

3. Toate elementele primului rând sunt împărțite la elementul superior al coloanei selectate.

4. Din rândurile rămase scădeți primul rând, înmulțit cu primul element al rândului corespunzător, pentru a obține primul element din fiecare rând (cu excepția primului) zero.

6. După repetarea acestei proceduri o dată, se obține o matrice triunghiulară superioară

7. Scădeți din penultimul rând ultimul rând, înmulțit cu coeficientul corespunzător, astfel încât doar 1 pe diagonala principală să rămână în penultimul rând.

8. Repetați pasul anterior pentru liniile următoare. Ca rezultat, se obține o matrice de identitate și o soluție în locul unui vector liber (este necesar să se efectueze toate aceleași transformări cu acesta).

9. Pentru a obține matricea inversă, trebuie să aplicați toate operațiile în aceeași ordine la matricea de identitate.

metoda Gauss

Din punct de vedere istoric, prima, cea mai comună metodă de rezolvare a sistemelor de ecuații liniare este metoda Gauss, sau metoda eliminării succesive a necunoscutelor. Esența acestei metode constă în faptul că prin eliminarea succesivă a necunoscutelor, sistemul dat este transformat într-un sistem în trepte (în special, triunghiular) echivalent cu cel dat. În rezolvarea practică a unui sistem de ecuații liniare prin metoda Gauss, este mai convenabil să se reducă la o formă treptată nu sistemul de ecuații în sine, ci matricea extinsă a acestui sistem, efectuând transformări elementare pe rândurile sale. Matricele obţinute succesiv în timpul transformării sunt de obicei legate printr-un semn de echivalenţă.

Exemplul 1.13. Rezolvați sistemul de ecuații folosind metoda Gauss: x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0.

Soluţie. Scriem matricea augmentată a acestui sistem

și efectuează următoarele transformări elementare pe rândurile sale: a) din al doilea și al treilea rând, scădeți primul, înmulțit cu 3, respectiv 2: ~ ;

b) înmulțiți al treilea rând cu (-5) și adăugați-l pe al doilea: .

Ca urmare a tuturor acestor transformări, acest sistem este redus la o formă triunghiulară: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.

Din ultima ecuație găsim z = -1,3. Înlocuind această valoare în a doua ecuație, avem y = -1,2. Mai departe de prima ecuație obținem x = - 0,7

DIN CAIET:

metoda Gauss

Metoda constă din două părți - înainte și înapoi.

Mișcarea directă constă în comportamentul de extindere a matricei SLE la o formă în trepte folosind transformări elementare de rând. Într-o matrice în trepte, fiecare rând următor are mai multe zerouri la început decât cel anterior - sau este zero

Exemplu:

Transformarea elementară a rândurilor matricei este:

1) adăugarea numerelor unui rând al matricei, înmulțite cu un anumit număr, la unul dintre rândurile inferioare ale matricei.

2) Schimbați două linii pe alocuri

Mișcarea inversă a metodei gaussiene constă în exprimarea secvențială a unor variabile în termenii altora, pornind de la linia zero de jos. Rezultatul este o soluție generală.

După cursa înainte, există 3 opțiuni pentru tipul în trepte al matricei extinse:

1) Fiecare linie următoare are la început cu exact cu un zero mai mult decât precedentul

Exemplu:

Scriem ecuația linie cu linie și începem să găsim valoarea variabilelor din linia de jos.

4X 4 \u003d 8Þ X 4 \u003d 2

Înlocuiți în ecuația anterioară

2X 3 -3X 4 \u003d -8 adică 2X 3 -3 * 2 \u003d -8 sau 2X 3 \u003d -2, Þ X 3 \u003d -1, înlocuiți X3 și X4 pe a doua linie etc. Obținem singura soluție a SLU

2) Numărul de rânduri diferite de zero este mai mic decât numărul de variabile. Atunci una dintre linii conține la început zerouri cu cel puțin 2 mai multe decât cea anterioară și considerăm că linia ulterioară nenulă nu are forma (0 ... 0 b) unde numărul b=0

De exemplu:

3) Ultima linie diferită de zero are forma (0…0/b), unde b=0 corespunde egalităților contradictorii o=b, deci sistemul este incompatibil

Rezolvarea SLE prin metoda Gauss

2X 1 + 3X 2 + X 3 \u003d 1

4X 1 + 5X 2 + 4X 3 = 7

6X 1 +10X 2 -3X 3 = -10

Compunem matricea extinsă a mișcării directe.

Calculul determinanților n-a comanda:

Conceptul de determinant n-a comanda

Folosind acest articol despre determinanți, veți învăța cu siguranță cum să rezolvați probleme precum următoarele:

Rezolvați ecuația:

și multe altele pe care profesorii le place atât de mult să vină.

Determinantul matriceal sau pur și simplu determinantul joacă un rol important în rezolvarea sistemelor de ecuații liniare. În general, determinanții au fost inventați în acest scop. Deoarece se spune adesea și „determinantul unei matrici”, vom menționa și aici matrice. Matricea este un tabel dreptunghiular format din numere care nu pot fi schimbate. O matrice pătrată este un tabel care are același număr de rânduri și coloane. Doar o matrice pătrată poate avea un determinant.

Este ușor de înțeles logica scrierii determinanților după următoarea schemă. Să luăm un sistem de două ecuații cu două necunoscute cunoscute de la școală:

În determinant, coeficienții pentru necunoscute se scriu secvențial: în prima linie - din prima ecuație, în a doua linie - din a doua ecuație:

De exemplu, dacă i se oferă un sistem de ecuații

atunci se formează următorul determinant din coeficienții necunoscutelor:

Deci, să presupunem că ni se oferă un tabel pătrat format din numere aranjate în n rânduri (rânduri orizontale) și în n coloane (rânduri verticale). Cu ajutorul acestor numere, după niște reguli, pe care le vom studia mai jos, găsesc un număr, pe care îl numesc determinant n de ordinul al-lea și sunt notate după cum urmează:

(1)

Se numesc numere elemente determinant (1) (primul indice înseamnă numărul rândului, al doilea - numărul coloanei, la intersecția căreia se află un element; i = 1, 2, ..., n; j= 1, 2, ..., n). Ordinea unui determinant este numărul de rânduri și coloane ale acestuia.

O linie dreaptă imaginară care leagă elementele determinantului pentru care ambii indici sunt aceiași, i.e. elemente

numit diagonala principală, cealaltă diagonală este latură.

Calculul determinanților de ordinul doi și trei

Să arătăm cum se calculează determinanții primelor trei ordine.

Determinantul de ordinul întâi este elementul însuși, adică

Cel de-al doilea determinant este numărul obținut după cum urmează:

, (2)

Produsul elementelor de pe diagonala principală și, respectiv, secundară.

Egalitatea (2) arată că produsul elementelor diagonalei principale se ia cu semnul său, iar produsul elementelor diagonalei secundare se ia cu semnul opus. .

Exemplul 1 Calculați determinanții de ordinul doi:

Soluţie. Prin formula (2) găsim:

Cel de-al treilea determinant este un număr obținut astfel:

(3)

Este greu de reținut această formulă. Cu toate acestea, există o regulă simplă numită regula triunghiului , ceea ce facilitează reproducerea expresiei (3). Notând elementele determinantului cu puncte, legăm prin segmente drepte pe acelea dintre ele care dau produsele elementelor determinantului (Fig. 1).

Formula (3) arată că produsele elementelor diagonalei principale, precum și elementele situate la vârfurile a două triunghiuri, ale căror baze sunt paralele cu aceasta, sunt luate cu semnele lor; cu cele opuse - produsele elementelor diagonalei secundare, precum și elementele situate la vârfurile a două triunghiuri care sunt paralele cu aceasta .

În fig.1, diagonala principală și bazele triunghiurilor corespunzătoare acesteia și diagonala laterală și bazele triunghiurilor corespunzătoare acesteia sunt evidențiate cu roșu.

La calcularea determinanților, este foarte important, ca și în liceu, să ne amintim că un număr minus înmulțit cu un număr minus are ca rezultat un semn plus, iar un semn plus înmulțit cu un număr minus dă un număr cu semnul minus.

Exemplul 2 Calculați determinantul de ordinul trei:

Soluţie. Folosind regula triunghiurilor, obținem

Calculul determinanților n-a comanda

Extinderea pe rând sau pe coloană a determinantului

Pentru a calcula determinantul n de ordinul a, este necesar să cunoașteți și să utilizați următoarea teoremă.

teorema lui Laplace. Determinantul este egal cu suma produselor elementelor oricărui rând și a complementelor lor algebrice, i.e.

Definiție. Dacă în determinant n a alege în mod arbitrar p linii şi p coloane ( p < n), atunci elementele de la intersecția acestor rânduri și coloane formează o matrice de ordine.

Determinantul acestei matrice se numește minor determinant original. De exemplu, luați în considerare determinantul:

Să construim o matrice din rânduri și coloane cu numere pare:

Determinant

numit minor determinant . A primit un minor de ordinul doi. Este clar că diverși minori din primul, al doilea și al treilea ordin pot fi construiți.

Dacă luăm un element și tăiem rândul și coloana la intersecția cărora se află în determinant, atunci obținem un minor, numit minorul elementului, pe care îl notăm cu:

.

Dacă minorul este înmulțit cu , unde 3 + 2 este suma numerelor rândurilor și coloanelor la intersecția cărora se află elementul, atunci produsul rezultat se numește adunare algebrică element și este notat cu ,

În general, minorul unui element va fi notat cu , iar complementul algebric cu ,

(4)

De exemplu, să calculăm complementele algebrice ale elementelor și determinantul de ordinul trei:

Prin formula (4) obținem

La descompunerea unui determinant, se folosește adesea următoarea proprietate a determinantului n-a ordinea:

dacă produsul elementelor corespunzătoare dintr-un alt rând sau coloană cu un factor constant este adăugat la elementele oricărui rând sau coloană, atunci valoarea determinantului nu se va modifica.

Exemplul 4

Să scădem preliminar elementele celui de-al patrulea rând din primul și al treilea rând, apoi vom avea

În a patra coloană a determinantului obținut, trei elemente sunt zerouri. Prin urmare, este mai profitabilă extinderea acestui determinant prin elementele coloanei a patra, deoarece primele trei produse vor fi zero. De aceea

Puteți verifica soluția cu calculator determinant online .

Și următorul exemplu arată cum calculul determinantului oricărui ordin (în acest caz, al patrulea) poate fi redus la calculul determinantului celui de-al doilea ordin.

Exemplul 5 Calculați determinantul:

Să scădem elementele primului rând din al treilea rând și să adăugăm elementele primului rând la elementele celui de-al patrulea rând, apoi vom avea

În prima coloană, toate elementele, cu excepția primului, sunt zerouri. Adică, determinantul poate fi deja descompus în prima coloană. Dar nu vrem să calculăm determinantul de ordinul trei. Prin urmare, vom face mai multe transformări: vom adăuga elementele celui de-al doilea rând înmulțit cu 2 la elementele celui de-al treilea rând și vom scădea elementele celui de-al doilea rând din elementele celui de-al patrulea rând. Ca urmare, determinantul, care este un complement algebric, poate fi el însuși extins în prima coloană și trebuie doar să calculăm determinantul de ordinul doi și să nu ne confundam în semne:

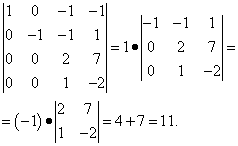
Aducerea determinantului într-o formă triunghiulară

Un determinant în care toate elementele aflate pe o parte a uneia dintre diagonale sunt egale cu zero se numește triunghiular. Cazul diagonalei secundare se reduce la cazul diagonalei principale prin inversarea ordinii rândurilor sau coloanelor. Un astfel de determinant este egal cu produsul elementelor diagonalei principale.

Pentru a reduce la o formă triunghiulară, se folosește aceeași proprietate a determinantului n a treia ordine, pe care am folosit-o în paragraful anterior: dacă adăugăm produsul elementelor corespunzătoare dintr-un alt rând sau coloană cu un factor constant la elementele oricărui rând sau coloană, atunci valoarea determinantului nu se va modifica.

Puteți verifica soluția cu calculator determinant online .

Proprietăți determinante n-a comanda

În cele două paragrafe precedente, am folosit deja una dintre proprietățile determinantului n-a comanda. În unele cazuri, pentru a simplifica calculul determinantului, puteți utiliza alte proprietăți importante ale determinantului. De exemplu, se poate reduce determinantul la suma a doi determinanți, unul sau ambii putând fi extins convenabil de-a lungul unui rând sau coloană. Există o mulțime de cazuri de astfel de simplificare, iar chestiunea utilizării uneia sau alteia proprietăți a determinantului ar trebui decisă individual.

Determinant de matrice (determinant matriceal) este un tabel pătrat de numere sau simboluri matematice ( Δd).

Definiție. determinant matriceal n×n este numarul:

Unde ( a 1 , a 2 ,...,α n) - permutarea numerelor din 1 inainte de n, N (α 1 ,α 2 ,...,α n)- numărul de inversiuni în permutare, însumarea are loc peste toate permutările posibile ale ordinului n.

Determinant de matrice A denumit practic ca de t(A), |A|, sau ?(A).

Parametri, cu ajutorul cărora se găsește soluția tuturor tipurilor de matrici algebrice.

La găsiți determinantul matricei este necesar să se cunoască proprietăţile de bază ale matricelor şi succesiunea acţiunilor la rezolvarea unei matrice.

1. Pentru matrice de ordine n=2 determinantul se găsește folosind formula: Δ= a11*un 22-a 12 *un 21
2. Pentru matrice de ordine n=3 determinantul se găseşte prin adunări algebrice sau folosind metoda Sarrus.
3. O matrice cu dimensiunea >3 se descompune în complemente algebrice, pentru care se găsesc determinanții lor (minori). De exemplu, determinantul unei matrice de ordinul 4 este calculat prin expansiune în rânduri sau coloane.

Pentru găsirea determinantului matriceal, care conține funcții în matrice, se folosesc metode standard. De exemplu, pentru a găsi determinantul unei matrice de ordinul al treilea:

Să folosim expansiunea pe prima linie:

Δ = sin(x) × + 1× = 2sin(x) cos(x) - 2cos(x) = sin(2x) - 2cos(x)

Calculați determinantul matricei.

Calculați determinantul matricei Există mai multe metode care sunt enumerate mai jos.

Cea mai populară modalitate de a calcula determinantul unei matrice este metoda de selectare a adunărilor algebrice. Există o versiune mai simplă a acestei metode - calculul determinantului folosind regula Sarrus. Aceste metode sunt diferite atunci când se calculează determinantul unei matrice simple mici, iar dacă trebuie să calculați o matrice de dimensiuni mari, atunci astfel de metode de calcul al determinantului matriceal:

• calculul determinantului prin metoda reducerii ordinului,
• calculul determinantului prin metoda Gauss (prin reducerea matricei la o formă triunghiulară),
• calculul determinantului prin metoda de descompunere.

În Excel, pentru a calcula determinantul, se folosește funcția = MOPRED (gamă de celule).