ВИЗНАЧНИК
або детермінант, - у математиці запис чисел як квадратної таблиці, у відповідність якої ставиться інше число ( " значення " визначника). Дуже часто під поняттям "визначник" мають на увазі як значення визначника, і форму його записи. Визначники дозволяють зручно записувати складні вирази, що виникають, наприклад, при вирішенні лінійних рівнянь в аналітичній геометрії та математичному аналізі. Відкриття визначників приписують японському математику С. Кова (1683) та, незалежно, Г. Лейбніцу (1693). Сучасна теорія походить від робіт Ж. Біне, О. Коші та К. Якобі на початку 19 ст. Найпростіший визначник складається з 4 чисел, званих елементами та розташованих у вигляді 2-х рядків та 2-х стовпців. Про такого визначника говорять, що він 2-го порядку. Наприклад, такий визначник

Значення якого дорівнює 2 * 5 - 3 * 1 (тобто 10 - 3 або 7). У випадку визначник 2-го порядку прийнято записувати як

А його значення дорівнює a1b2 – a2b1, де a та b – числа або функції. Визначник 3-го порядку складається з 9 елементів, розташованих у вигляді 3-х рядків та 3-х стовпців. У випадку визначник n-го порядку складається з n2 елементів, і його записують як

Перший індекс кожного елемента вказує номер рядка, другий – номер стовпця, на перетині яких стоїть цей елемент, тому aij – елемент i-го рядка та j-го стовпця. Часто такий визначник записують як |aij|. Один з методів обчислення визначника, що майже завжди використовується при обчисленні визначників високого порядку, полягає в розкладанні "мінорів". Мінором, що відповідає будь-якому елементу визначника, називається визначник меншого на 1 порядку, що отримується з вихідного викреслювання рядка і стовпця, на перетині яких стоїть цей елемент. Наприклад, мінором, що відповідає елементу a2 з визначника

"Алгебраїчним доповненням" елемента називається його мінор, взятий зі знаком плюс, якщо сума номерів рядка та стовпця, на перетині яких стоїть елемент, парна, та зі знаком мінус, якщо вона непарна. У наведеному вище прикладі елемент a2 полягає в 1-му стовпці та у 2-му рядку; сума (1 + 2) непарна, тому алгебраїчне доповнення елемента a2 дорівнює його мінору, взятому зі знаком мінус, тобто.

Значення визначника дорівнює сумі творів елементів будь-якого рядка (або будь-якого стовпця) на їх додатки алгебри. Наприклад, визначник

розкладений по першому стовпцю, має вигляд

а його розкладання по другому рядку, має вигляд

Обчисливши кожен мінор і помноживши його на коефіцієнт, неважко переконатися, що обидва висловлювання збігаються. Значення визначника. Під значенням визначника

Прийнято розуміти суму всіх творів із n елементів, тобто.

У цій формулі підсумовування ведеться за всіма перестановками j1, ?, jn чисел 1, 2, ?, n і перед членом ставиться знак плюс, якщо перестановка парна, і мінус, якщо ця перестановка непарна. Така сума нараховує рівно n! членів, половина яких береться зі знаком плюс, половина – зі знаком мінус. Кожен член суми містить по одному члену з кожного стовпця та кожного рядка визначника. Можна довести, що ця сума збігається з виразом, що отримується при розкладанні визначника по мінорах.
Властивості визначника.Серед найважливіших властивостей визначника назвемо такі. (i) Якщо всі елементи будь-якого рядка (або будь-якого стовпця) дорівнюють нулю, то і значення визначника дорівнює нулю:

(ii) Якщо елементи двох рядків (або двох стовпців) рівні або пропорційні, значення визначника дорівнює нулю:

(iii) Значення визначника не зміниться, якщо його рядки і стовпці поміняти місцями, тобто. записати перший рядок у вигляді першого стовпця, другий рядок – у вигляді другого стовпця тощо. (Така операція називається транспонуванням). Наприклад,

(iv) Значення визначника не зміниться, якщо до елементів одного рядка (або стовпця) додати відповідні елементи іншого рядка (або стовпця), помножені на довільний множник. У наступному прикладі елементи другого рядка множаться на -2 і додаються до елементів першого рядка:

(v) Якщо поміняти місцями два рядки (або два стовпці), то визначник змінить знак:

(vi) Якщо всі елементи одного рядка (або одного стовпця) містять спільний множник, цей множник можна винести за знак визначника:

приклад. Обчислимо значення наступного визначника 4-го порядку:

Додамо до 1-го рядка 4-й рядок:

Віднімемо 1-й стовпець з 4-го стовпця:

Помножимо 3-й стовпець на 3 і віднімемо з 4-го стовпця:

Якщо завгодно, то рядки та стовпці можна поміняти місцями:

Розкладемо визначник за елементами четвертого рядка. Три елементи цього рядка рівні нулю, ненульовий елемент стоїть у третьому стовпці, а оскільки сума (3 + 4) непарна, його додаток алгебри має знак мінус. В результаті отримуємо:

Мінор можна розкласти по елементах третього рядка: два її елементи дорівнюють нулю, а відмінний від нуля елемент стоїть у третьому стовпці; сума (3 + 3) парна, тому попередню рівність можна продовжити:

Застосування. Вирішення системи рівнянь

можна отримати, якщо перше рівняння помножити на b2, друге - на b1, а потім відняти одне рівняння від іншого. Зробивши ці операції, ми отримаємо

Або, якщо

то

Такий запис рішення з допомогою визначників допускає узагальнення у разі рішення системи n лінійних рівнянь з n невідомими; кожен визначник буде n-го порядку. Визначником системи лінійних рівнянь

буде

Зауважимо, що й D = 0, то рівняння або несумісні, або є незалежними. Тому попереднє обчислення визначника D дозволяє перевірити, чи дозволяється система лінійних рівнянь.
Визначники у аналітичній геометрії.Загальне рівняння конічного перерізу представимо у вигляді

Визначник

називається дискримінантом. Якщо D = 0, то крива вироджується в пару паралельних або прямих, що перетинаються, або в точку (див. також КОНІЧНІ ПЕРЕЧЕННЯ). Інший приклад: площа трикутника A з вершинами в точках (обхід - проти годинникової стрілки) (x1, y1), (x2, y2) та (x3, y3) визначається виразом

Зв'язок визначників із матрицями.Матрицею називається запис масиву чисел як прямокутної таблиці. Визначники пов'язані із квадратними матрицями; наприклад, визначник матриці

Якщо A, B і З - квадратні матриці, то |A|*|B| = | C |.
Див. такожАлгебра абстрактна .
Якобіан.Якщо x = f(u, v), y = g(u, v) – перетворення координат, то визначник

Називається якобіаном чи визначником Якобі цього перетворення. Якщо J не дорівнює 0 в деякій точці, то її околиці рівняння перетворення можна однозначно дозволити щодо u і v, представивши їх як функції від x і y.
Див. МАТЕМАТИЧНИЙ АНАЛІЗ.

Енциклопедія Кольєра. - Відкрите суспільство. 2000 .

Синоніми:

Дивитися що таке "ВИЗНАЧНИК" в інших словниках:

ВИЗНАЧНИК, визначника, чоловік. (книжн.). 1. Те, що визначає, виражає собою щось. 2. Книга, що служить для довідок щодо чогось (научн.). Визначник рослин. Визначник грибів. 3. Вираз, що складається з ... Тлумачний словник Ушакова

- (Детермінант) складений за певним правилом з n2 чисел математичний вираз, що застосовується при вирішенні та дослідженні систем алгебраїчних рівнянь 1-го ступеня. Число n називається порядком визначника. Так, визначник 2 го порядку. Великий Енциклопедичний словник

Розпізнавець, гесіан, мінор, детермінант Словник російських синонімів. визначник сут., кіль у синонімів: 10 автовизначник (1) … Словник синонімів

ВИЗНАЧНИК- (Детермінант) складений за певним правилом з n2 чисел математичний вираз, що застосовується при вирішенні та дослідженні систем алгебраїчних рівнянь 1-го ступеня. Число п називається порядком визначника. Так, визначник 2 го порядку. Велика політехнічна енциклопедія

ВИЗНАЧНИК, я, чоловік. 1. Пристрій визначення чого н., а також взагалі те, за допомогою чого можна що н. точно визначити, встановити. Телефон із визначником номера. О. ритму. 2. Книга для довідок щодо чого н. (Спец.). О. рослин … Тлумачний словник Ожегова

- (Детермінант) квадратної матриці А = | | aij | | порядку n, detA багаточлен ... Фізична енциклопедія

визначник- - Тематики електрозв'язок, основні поняття EN determinant ... Довідник технічного перекладача

Цей термін має й інші значення, див. Визначник (значення). Визначник (або детермінант) є одним з основних понять лінійної алгебри. Визначник матриці є багаточленом від елементів квадратної матриці (тобто такий, у … Вікіпедія

визначник- 3.4.6 визначник (auxiliary): Код допоміжного класу УДК. Джерело … Словник-довідник термінів нормативно-технічної документації

Я; м. 1. Книжковий. Те, чим визначається, визначається що л. Звук може бути визначником швидкості. Головним визначником часу є рух Сонця у космічному просторі. 2. Спец. Керівництво (книга чи таблиця) для визначення чого… Енциклопедичний словник

Книжки

• Визначник покритонасінних деревних рослин за плодами та насінням, Синіцин Євген Михайлович. Визначник складається із двох частин. Перша частина являє собою таблицю для визначення пологів, а друга включає таблиці для визначення видів покритонасінних деревних рослин.

· Визначником квадратний матриці А п-го порядку або визначником п-го порядку називається число, що дорівнює алгебраїчній сумі п! членів, кожен із яких є твором пелементів матриці, взятих по одному з кожного рядка та кожного стовпця з певними знаками. Визначник позначається або .

Визначник другого порядкує число, виражене так: . Наприклад .

Визначник третього порядкуобчислюється за правилом трикутників (правило Саррюса): .

Приклад. .

Зауваження. Фактично визначники третього порядку, як і вищих порядків, обчислюються з допомогою властивостей визначників.

Властивості визначників п-го порядку.

1. Величина визначника не зміниться, якщо кожен рядок (стовпець) замінити стовпцем (рядком) з тим самим номером – транспонувати.

2. Якщо один із рядків (стовпець) визначника складається з нулів, то величина визначника дорівнює нулю.

3. Якщо у визначнику поміняти місцями два рядки (стовпці), то абсолютна величина визначника не зміниться, а знак зміниться на протилежний.

4. Визначник, що містить два однакові рядки (стовпця), дорівнює нулю.

5. Загальний множник всіх елементів рядка (стовпця) можна винести за знак визначника.

· Мінором деякого елемента визначника п-го порядку називається визначник ( п-1)-го порядку, отриманий з вихідного викреслювання того рядка і того стовпця, на перетині яких знаходиться обраний елемент. Позначення: .

· Алгебраїчним доповненням елементом визначника називається його мінор, взятий зі знаком . Позначення: В.о. =.

6. Визначник квадратної матриці дорівнює сумі творів елементів будь-якого рядка (або стовпця) на їх додатки алгебри ( теорема розкладання).

7. Якщо кожен елемент - того рядка є сумою kдоданків, то визначник подається у вигляді суми kвизначників, у яких усі рядки, крім того рядка, такі ж як у вихідному визначнику, а той рядок у першому визначнику складається з перших доданків, у другому – з других і т.д. Те ж саме і для стовпців.

8. Визначник не зміниться, якщо до одного з рядків (стовпців) додати інший рядок (стовпець), помножений на число .

Слідство. Якщо до рядка (стовпця) визначника додати лінійну комбінацію інших її рядків (стовпців), то визначник не зміниться.

9. Визначник діагональної матриці дорівнює добутку елементів, що стоять на головній діагоналі, тобто.

Зауваження. Визначник трикутної матриці також дорівнює добутку елементів, що стоять на головній діагоналі.

Перераховані властивості визначників дозволяють значно спростити їхнє обчислення, що особливо важливо для визначників високих порядків. При цьому доцільно так перетворити вихідну матрицю, щоб перетворена матриця мала рядок або стовпець, що містить якомога більше нулів (обнулення рядків або стовпців).

приклади.Обчислимо ще раз визначник, наведений у попередньому прикладі, використовуючи властивості визначників.

Рішення: Зауважимо, що у першому рядку є загальний множник – 2, а у другому – загальний множник 3, винесемо їх за знак визначника (за властивістю 5). Далі розкладемо визначник, наприклад, першого стовпця, використовуючи властивість 6 (теорему розкладання).

Найбільш ефективний метод приведення визначника до діагонального або трикутного вигляду . Для обчислення визначника матриці достатньо виконати таке перетворення матриці, яке не змінить визначника і дозволить перетворити матрицю на діагональну.

У висновку зауважимо, що якщо визначник квадратної матриці дорівнює нулю, то матриця називається виродженою (або особливою) , в іншому випадку - невиродженою .

1. Визначник не змінюється під час транспонування.

2. Якщо один із рядків визначника складається з нулів, то визначник дорівнює нулю.

3. Якщо в визначнику переставити два рядки, визначник змінить знак.

4. Визначник, що містить два однакові рядки, дорівнює нулю.

5. Якщо всі елементи деякого рядка визначника помножити на деяке число k, сам визначник помножиться на k.

6. Визначник, що містить два пропорційні рядки, дорівнює нулю.

7. Якщо всі елементи i-го рядка визначника представлені у вигляді суми двох доданків aij = bj + cj (j= ), то визначник дорівнює сумі визначників, у яких усі рядки, крім i-ого, - такі ж, як у заданому визначнику , а i-й рядок в одному з доданків складається з елементів bj, в іншому - з елементів cj.

8. Визначник не змінюється, якщо до елементів одного з його рядків додаються відповідні елементи іншого рядка, помножені на те саме число.

Зауваження.Усі властивості залишаються справедливими, якщо замість рядків взяти стовпці.

Мінором M i j елемента a i j визначника d n-го порядку називається визначник порядку n-1, який виходить із d викреслюванням рядка та стовпця, що містять даний елемент.

Алгебраїчним доповненнямелемента a i j визначника d називається його мінор M i j взятий зі знаком (-1) i + j . Алгебраїчне доповнення елемента a i j позначатимемо A i j . Таким чином, A i j = (-1) i + j M i j .

Способи практичного обчислення визначників, засновані на тому, що визначник n може бути виражений через визначники нижчих порядків, дає наступна теорема.

Теорема (Розкладання визначника по рядку або стовпцю).

Визначник дорівнює сумі творів всіх елементів довільного його рядка (або стовпця) з їхньої алгебраїчні доповнення. Інакше кажучи, має місце розкладання d за елементами i-го рядка d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = )

або j-го стовпця d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).

Зокрема, якщо всі елементи рядка (або стовпця), крім одного, дорівнюють нулю, то визначник дорівнює цьому елементу, помноженому на його додаток алгебри.

приклад 1.4.Не рахуючи визначника , показати, що він дорівнює нулю Рішення.Віднімемо з другого рядка перший, отримаємо визначник , рівний вихідному. Якщо з третього рядка також відняти перший, то вийде визначник , У якому два рядки пропорційні. Такий визначник дорівнює нулю.

приклад 1.5.Обчислити визначник D = , Розклавши його за елементами другого стовпця.

Рішення.Розкладемо визначник за елементами другого стовпця:

D = a 12 A 12 + a 22 A 22 + a 32 A 32 =

приклад 1.6.Обчислити визначник

A =
,В якому всі елементи з одного боку від головної діагоналі рівні нулю. Рішення.Розкладемо визначник А за першим рядком: A = a 11 A 11 = . Визначник, що стоїть праворуч, можна розкласти по першому рядку, тоді отримаємо:

A =
.І так далі. Після n кроків прийдемо до рівності A = а 11 а 22... a nn.

3.Основні поняття систем лінійних рівнянь. Теорема Крамер.

Визначення. Система лінійних рівнянь- це об'єднання з nлінійних рівнянь, кожне з яких містить kзмінних. Записується це так:

Багато хто, вперше стикаючись з вищою алгеброю, помилково вважають, що число рівнянь обов'язково має співпадати з кількістю змінних. У шкільній алгебрі так і буває, проте для вищої алгебри це, взагалі кажучи, неправильно.

Визначення. Вирішення системи рівнянь- це послідовність чисел ( k 1 ,k 2 , ..., k n), що рішенням кожного рівняння системи, тобто. при підстановці до цього рівняння замість змінних x 1 , x 2 , ..., x nдає правильну числову рівність.

Відповідно, розв'язати систему рівнянь- значить знайти безліч її рішень або довести, що це безліч порожньо. Оскільки кількість рівнянь та кількість невідомих може не співпадати, можливі три випадки:

1. Система несумісна, тобто. безліч всіх рішень порожня. Досить рідкісний випадок, який легко виявляється незалежно від цього, яким методом вирішувати систему.

2. Система спільна та визначена, тобто. має рівно одне рішення. Класичний варіант добре відомий ще зі шкільної лави.

3. Система спільна і визначено, тобто. має безліч рішень. Це найжорсткіший варіант. Недостатньо вказати, що «система має безліч рішень» - треба описати, як влаштовано це безліч.

Визначення. Змінна x iназивається дозволеної, Якщо вона входить тільки в одне рівняння системи, причому з коефіцієнтом 1. Іншими словами, в інших рівняннях коефіцієнт при змінній x iповинен дорівнювати нулю.

Якщо в кожному рівнянні вибрати одну дозволену змінну, отримаємо набір дозволених змінних для всієї системи рівнянь. Сама система, записана в такому вигляді, теж називатиметься дозволеною. Взагалі кажучи, ту саму вихідну систему можна звести до різних дозволених, проте зараз нас це не хвилює. Ось приклади дозволених систем:

Обидві системи є дозволеними щодо змінних x 1 , x 3 та x 4 . Втім, з тим самим успіхом можна стверджувати, що друга система - дозволена щодо x 1 , x 3 та x 5 . Достатньо переписати останнє рівняння у вигляді x 5 = x 4 .

Тепер розглянемо загальніший випадок. Нехай у нас kзмінних, з яких rє дозволеними. Тоді можливі два випадки:

1. Число дозволених змінних rодно загальному числу змінних k: r = k. Отримуємо систему з kрівнянь, у яких r = kдозволених змінних. Така система є спільною та певною, т.к. x 1 = b 1 , x 2 = b 2 , ..., x k = b k;

2. Число дозволених змінних rменше загальної кількості змінних k: r < k. Інші ( k − r) змінних називаються вільними - можуть приймати будь-які значення, у тому числі легко обчислюються дозволені змінні.

Так, у наведених вище системах змінні x 2 , x 5 , x 6 (для першої системи) та x 2 , x 5 (для другої) є вільними. Випадок, коли є вільні змінні, краще сформулювати як теореми…

Як вирішити? – Вирішення системи лінійних рівнянь методом підстановки («шкільний метод»).
– Рішення системи методом почленного складання (віднімання) рівнянь системи.
-Рішення системи за формулами Крамера.
-Рішення системи за допомогою зворотної матриці.
-Рішення системи методом Гауса.

КРАМІР

Спочатку розглянемо правило Крамера для системи двох лінійних рівнянь із двома невідомими. Існують системи лінійних рівнянь із двома змінними, які доцільно вирішувати саме за правилом Крамера!

Розглянемо систему рівнянь

На першому кроці обчислимо визначник, його називають головним визначником системи.

Якщо , то система має безліч рішень або несумісна (не має рішень). В цьому випадку правило Крамера не допоможе, потрібно використовувати метод Гауса.

Якщо , то система має єдине рішення, і для знаходження коріння ми повинні обчислити ще два визначники: і

На практиці вищезазначені визначники також можуть позначатися латинською літерою.

Коріння рівняння знаходимо за формулами:

Приклад 7

Розв'язати систему лінійних рівнянь

Ми бачимо, що коефіцієнти рівняння досить великі, у правій частині присутні десяткові дроби з комою. Кома - досить рідкісний гість у практичних завданнях з математики, цю систему я взяв з економетричного завдання.

Як вирішити таку систему? Можна спробувати висловити одну змінну через іншу, але в цьому випадку, напевно, вийдуть страшні накручені дроби, з якими вкрай незручно працювати, та й оформлення рішення виглядатиме просто жахливо. Можна помножити друге рівняння на 6 і провести почленное віднімання, але й тут виникнуть ті самі дроби.

Що робити? У таких випадках і приходять на допомогу формули Крамера.

Виходить, система має єдине рішення.

;

;

Як бачите, коріння вийшло ірраціональним, і знайдено приблизно, що цілком прийнятно (і навіть буденно) для завдань економетрики.

Коментарі тут не потрібні, оскільки завдання вирішується за готовими формулами, однак є один нюанс. Коли використовуєте цей метод, обов'язковимфрагментом оформлення завдання є наступний фрагмент: « Отже, система має єдине рішення» . В іншому випадку рецензент може Вас покарати за неповагу до теореми Крамера.

Зовсім не зайвою буде перевірка, яку зручно провести на калькуляторі: підставляємо наближені значення у ліву частину кожного рівняння системи. В результаті з невеликою похибкою повинні вийти числа, що знаходяться у правих частинах.

Формули Крамера

Метод Крамера у тому, що ми послідовно знаходимо головний визначник системи(5.3), тобто. визначник матриці А

і n допоміжних визначників D i (i= ), що виходять з визначника D заміною i-го стовпця стовпцем вільних членів.

Формули Крамера мають вигляд:

D x x i = D i (i = ). (5.4)

З (5.4) випливає правило Крамера, яке дає вичерпну відповідь на питання про спільність системи (5.3): якщо головний визначник системи відмінний від нуля, то система має єдине рішення, яке визначається за формулами:

Якщо головний визначник системи D і всі допоміжні визначники D i = 0 (i = ), система має безліч рішень. Якщо головний визначник системи D = 0, хоча б один допоміжний визначник відмінний від нуля, то система несовместна.

Приклад 1.14. Розв'язати методом Крамера систему рівнянь:

x 1 + x 2 + x 3 + x 4 = 5, x 1 + 2x 2 - x 3 + 4x 4 = -2, 2x 1 - 3x 2 - x 3 - 5x 4 = -2, 3x 1 + x 2 + 2x3 + 11x4 = 0.

Рішення.Головний визначник цієї системи D = = -142 ? 0, отже, система має єдине рішення. Обчислимо допоміжні визначники D i (i= ), що виходять з визначника D шляхом заміни в ньому стовпця, що складається з коефіцієнтів при x i, стовпцем із вільних членів: D 1 = = - 142, D 2 = = - 284, D 3 = = - 426,

D 4 = = 142. Звідси x 1 = D 1 /D = 1, x 2 = D 2 /D = 2, x 3 = D 3 /D = 3, x 4 = D 4 /D = -1, рішення системи - вектор С =(1, 2, 3, -1) T .

Основні поняття систем лінійних рівнянь. Метод гауса.

ДИВИСЬ ВИЩЕ.

Метод Гауса - Жордана(Метод повного виключення невідомих) - метод, який використовується для вирішення квадратних систем лінійних рівнянь алгебри, знаходження зворотної матриці, знаходження координат вектора в заданому базисі або відшукання рангу матриці. Метод є модифікацією методу Гауса.

Алгоритм

1. Вибирають перший ліворуч стовпець матриці, у якому є хоч одне відмінне від нуля значення.

2. Якщо найвище число в цьому стовпці є нуль, то змінюють перший рядок матриці з іншим рядком матриці, де в цій колонці немає нуля.

3. Всі елементи першого рядка поділяються на верхній елемент вибраного стовпця.

4. З рядків, що залишилися, віднімають перший рядок, помножений на перший елемент відповідного рядка, з метою отримати першим елементом кожного рядка (крім першого) нуль.

6. Після повторення цієї процедури вдруге отримують верхню трикутну матрицю

7. Віднімаємо з передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, для того, щоб у передостанньому рядку залишилася лише 1 на головній діагоналі.

8. Повторюють попередній крок для наступних рядків. У результаті отримують одиничну матрицю і рішення на місці вільного вектора (з ним необхідно проводити ті самі перетворення).

9. Щоб отримати зворотну матрицю, потрібно застосувати всі операції у тому порядку до одиничної матриці.

Метод Гауса

Історично першим, найпоширенішим методом розв'язання систем лінійних рівнянь є метод Гауса, або метод послідовного виключення невідомих. Сутність цього методу полягає в тому, що за допомогою послідовних винятків невідомих дана система перетворюється на ступінчасту (зокрема, трикутну) систему, рівносильну даній. При практичному вирішенні системи лінійних рівнянь методом Гауса зручніше приводити до ступінчастого вигляду не саму систему рівнянь, а розширену матрицю цієї системи, виконуючи елементарні перетворення над її рядками. Послідовно отримані в ході перетворення матриці з'єднують знаком еквівалентності.

Приклад 1.13. Розв'язати систему рівнянь методом Гауса: x + y – 3z = 2, 3x – 2y + z = – 1, 2x + y – 2z = 0.

Рішення.Випишемо розширену матрицю даної системи

і зробимо такі елементарні перетворення над її рядками: а) з її другого та третього рядків віднімемо перший, помножений відповідно на 3 і 2: ~ ;

б) третій рядок помножимо на (-5) і додамо до нього другий: .

В результаті всіх цих перетворень дана система приводиться до трикутного вигляду: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13.

З останнього рівняння знаходимо z = –1,3. Підставляючи це значення на друге рівняння, маємо y = -1,2. Далі з першого рівняння отримаємо x = – 0,7

З ЗОТРАДИ:

Метод Гауса

Метод складається з двох частин-прямого та зворотного ходу.

Прямий хід полягає у поведінці розширення матриці СЛУ до ступінчастого вигляду за допомогою елементарних перетворень рядків. У ступінчастому вигляді матриці кожен наступний рядок має на початку нулів більше, ніж попередній - або він нульовий

Приклад:

Елементарні перетворення рядків матриці-це:

1) додавання чисел одного рядка матриці, помножені на якесь число, до одного з нижніх рядків матриці.

2) Зміна двох рядків місцями

Зворотний хід методу Гауса полягає в послідовному вираженні одних змінних через інших, починаючи з нижнього нульового рядка. В результаті виходить загальне рішення.

Після прямого ходу можливі 3 варіанти ступінчастого виду розширеної матриці:

1)Кожна слід.рядок має на початку рівно не один нуль більше, ніж попередній

Приклад:

Записуємо по рядках рівняння і починаємо знаходити значення змінних з нижнього рядка.

4Х 4 =8Þ Х 4 =2

Підставляємо у попереднє рівняння

2Х3-3Х4=-8 тобто. 2Х 3 -3 * 2=-8 або 2Х 3 =-2, Х 3 =-1, підставляємо Х3 і Х4 в другий рядок і т.д. Отримуємо єдине рішення СЛУ

2) Число ненульових рядків менше кількості змінних. Тоді одні з рядків містить на початку нулів принаймні на 2 більше за попередній і вважаємо, що наступний ненульовий рядок не має вигляд(0…0 b) де число b=0

Наприклад:

3) Останній ненульовий рядок має вигляд (0 ... 0 / b), де b = 0 їй відповідає суперечливі рівності про = b, тому система несумісна

Рішення СЛУ методом Гауса

2Х1 +3Х2 +Х3 =1

4Х1 +5Х2 +4Х3 =7

6Х1+10Х2-3Х3=-10

Складаємо розширену матрицю прямий хід.

Обчислення визначників n-го порядку:

Поняття визначника n-го порядку

Користуючись цією статтею про визначників, ви обов'язково навчитеся вирішувати завдання на кшталт наступного:

Розв'язати рівняння:

та багатьох інших, які так люблять вигадувати викладачі.

Визначник матриці або просто визначник грає важливу роль у вирішенні систем лінійних рівнянь. Загалом визначники і були придумані для цієї мети. Оскільки часто кажуть також "визначник матриці", згадаємо тут і матриці. Матриця- Це прямокутна таблиця, складена з чисел, які не можна міняти місцями. Квадратна матриця - таблиця, у якій число рядків та число стовпців однаково. Визначник може бути лише у квадратної матриці.

Зрозуміти логіку запису визначників легко за наступною схемою. Візьмемо знайому вам зі шкільної лави систему із двох рівнянь із двома невідомими:

У визначнику послідовно записуються коефіцієнти за невідомих: у першому рядку - з першого рівняння, у другому рядку - з другого рівняння:

Наприклад, якщо дана система рівнянь

то з коефіцієнтів при невідомих формується наступний визначник:

Отже, нехай дана квадратна таблиця, що складається з чисел, розташованих у nрядках (горизонтальних рядах) та в nстовпчиках (вертикальних рядах). За допомогою цих чисел за деякими правилами, які ми вивчимо нижче, знаходять число, яке називають визначником n-го порядку і позначають так:

(1)

Числа називають елементамивизначника (1) (перший індекс означає номер рядка, другий – номер стовпця, на перетині яких стоїть елемент; i = 1, 2, ..., n; j= 1, 2, …, n). Порядок визначника – це його рядків і стовпців.

Уявна пряма, що з'єднує елементи визначника, які обидва індексу однакові, тобто. елементи

називається головною діагоналлю, інша діагональ – побічний.

Обчислення визначників другого та третього порядків

Покажемо, як обчислюються визначники перших трьох порядків.

Визначник першого порядку – це елемент тобто.

Визначник другого порядку є число, яке отримується таким чином:

, (2)

Добуток елементів, що стоять відповідно на головній та на побічній діагоналях.

Рівність (2) показує, що зі своїм знаком береться добуток елементів головної діагоналі, а з протилежним – добуток елементів побічної діагоналі .

приклад 1.Обчислити визначники другого порядку:

Рішення. За формулою (2) знаходимо:

Визначник третього порядку – це число, яке отримується так:

(3)

Запам'ятати цю формулу важко. Однак існує просте правило, зване правилом трикутників , що дозволяє легко відтворити вираз (3). Позначаючи елементи визначника точками, з'єднаємо відрізками прямої ті з них, які дають добуток елементів визначника (рис. 1).

Формула (3) показує, що зі своїми знаками беруться добутки елементів головної діагоналі, а також елементів, розташованих у вершинах двох трикутників, основи яких їй є паралельними; із протилежними – твори елементів побічної діагоналі, а також елементів, розташованих у вершинах двох трикутників, які їй паралельні .

На рис.1 головна діагональ та відповідні їй основи трикутників та побічна діагональ та відповідні їй основи трикутників виділені червоним кольором.

При обчисленні визначників дуже важливо, як і в середній школі, пам'ятати, що число зі знаком мінус, помножене на число зі знаком мінус, в результаті дає число зі знаком плюс, а число зі знаком плюс, помножене на число зі знаком мінус, в результаті дає число зі знаком мінус.

приклад 2.Обчислити визначник третього порядку:

Рішення. Користуючись правилом трикутників, отримаємо

Обчислення визначників n-го порядку

Розкладання визначника по рядку або стовпцю

Для обчислення визначника n-го порядку необхідно знати та використовувати наступну теорему.

Теорема Лапласа.Визначник дорівнює сумі творів елементів будь-якого рядка з їхньої алгебраїчні доповнення, тобто.

Визначення. Якщо у визначнику n-го порядку вибрати довільно pрядків та pстовпців ( p < n), то елементи, що знаходяться на перетині цих рядків та стовпців, утворюють матрицю порядку .

Визначник цієї матриці називається мінором вихідного визначника. Наприклад, розглянемо визначник:

З рядків та стовпців з парними номерами збудуємо матрицю:

Визначник

називається міноромвизначника. Отримали мінор другого порядку. Ясно, що можна побудувати різні мінори першого, другого і третього порядку.

Якщо взяти елемент і викреслити в визначнику рядок і стовпець, на перетині яких він стоїть, отримаємо мінор, званий мінором елемента , який позначимо через :

.

Якщо мінор помножити на , де 3 + 2 – сума номерів рядка та стовпця, на перетині яких стоїть елемент, то отриманий твір називається алгебраїчним доповненнямелемента і позначається ,

Взагалі, мінор елемента будемо позначати , а додаток алгебри ,

(4)

Наприклад обчислимо алгебраїчні доповнення елементів та визначника третього порядку:

За формулою (4) отримаємо

При розкладанні визначника часто використовується така властивість визначника n-го порядку:

якщо до елементів будь-якого рядка чи стовпця додати добуток відповідних елементів іншого рядка чи стовпця на постійний множник, то значення визначника не зміниться.

Приклад 4.

Попередньо віднімемо з першого і третього рядків елементи четвертого рядка, тоді матимемо

У четвертому стовпці отриманого визначника три елементи – нулі. Тому вигідніше розкласти цей визначник за елементами четвертого стовпця, тому що три перші твори будуть нулями. Тому

Перевірити рішення можна за допомогою калькулятора визначників онлайн .

На наступному прикладі показано, як обчислення визначника будь-якого (у разі - четвертого) порядку можна звести до обчислення визначника другого порядку.

Приклад 5.Обчислити визначник:

Віднімемо з третього рядка елементи першого рядка, а до елементів четвертого рядка додамо елементи першого рядка, тоді матимемо

У першому стовпці всі елементи, крім першого, – нулі. Тобто визначник можна вже розкласти по першому стовпцю. Але нам не хочеться обчислювати визначник третього порядку. Тому зробимо ще перетворення: до елементів третього рядка додамо елементи другого рядка, помножені на 2, та якщо з елементів четвертого рядка віднімемо елементи другого рядка. В результаті визначник, що є додатком алгебри, сам може бути розкладений по першому стовпцю і нам залишиться тільки обчислити визначник другого порядку і не заплутатися в знаках:

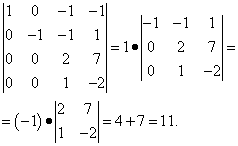
Приведення визначника до трикутного вигляду

Визначник, де всі елементи, що лежать з одного боку однієї з діагоналей, дорівнюють нулю, називається трикутним. Випадок побічної діагоналі шляхом зміни порядку рядків або стовпців на зворотний зводиться до нагоди головної діагоналі. Такий визначник дорівнює добутку елементів головної діагоналі.

Для приведення до трикутного вигляду використовується та сама властивість визначника n-го порядку, який ми застосовували у попередньому параграфі: якщо до елементів будь-якого рядка чи стовпця додати добуток відповідних елементів іншого рядка чи стовпця на постійний множник, то значення визначника не зміниться.

Перевірити рішення можна за допомогою калькулятора визначників онлайн .

Властивості визначника n-го порядку

У двох попередніх параграфах ми вже використовували одну з властивостей визначника n-го порядку. У деяких випадках для спрощення обчислення визначника можна скористатися іншими найважливішими властивостями визначника. Наприклад, можна привести визначник до суми двох визначників, з яких один або обидва можуть бути зручно розкладені по рядку або стовпцю. Випадків такого спрощення достатньо і вирішувати питання використання тієї чи іншої властивості визначника слід індивідуально.

Визначник матриці (детермінант матриці) - це квадратна таблиця чисел або математичних знаків ( Δd).

Визначення. Визначником матриці n×nє число:

де ( α 1 , α 2 ,...,α n) - перестановка чисел від 1 до n, N (α 1 ,α 2 ,...,α n)- число інверсій у перестановці, підсумовування відбувається за всіма можливими перестановками порядку n.

Визначник матриці Aв основному позначають як de t(A), |A|, або ?(A).

Параметри, з яких перебуває рішення всіх видів алгебраїчних матриць.

Щоб знайти визначник матрицінеобхідно знати основні властивості матриць та послідовність дій при вирішенні матриці.

1. Для матриць порядку n=2визначник знаходять за допомогою формули: Δ= a 11*a 22 -a 12*a 21
2. Для матриць порядку n=3визначник знаходять через алгебраїчні доповнення або за допомогою методу Саррюса.
3. Матриця з розмірністю >3 розкладається на додатки алгебри, для яких знаходяться свої визначники (мінори). Наприклад, визначник матриці 4 системи обчислюється через розкладання рядками чи стовпцям.

Для знаходження визначника матриці, що містить у матриці функції, використовуються стандартні методи. Наприклад, визначити визначник матриці третього порядку:

Скористаємося розкладанням за першим рядком:

Δ = sin(x) × + 1× = 2sin(x) cos(x) - 2cos(x) = sin(2x) - 2cos(x)

Обчислити визначник матриці.

Обчислити визначник матриціможна кількома методами, що будуть перераховані нижче.

Найпопулярнішим способом обчислення визначника матриці є метод підбору додатків алгебри. Існує більш проста версія цього методу - обчислення визначника за допомогою правила Саррюса. Ці методи відмінні при обчисленні визначника простої невеликої матриці, а якщо потрібно порахувати матрицю великої розмірності, можуть застосовуватися такі методи обчислення визначника матриці:

• обчислення визначника шляхом зниження порядку,
• обчислення визначника методом Гауса (через приведення матриці до трикутного вигляду),
• обчислення визначника методом декомпозиції.

У Excel до розрахунку визначника використовується функція =МОПРЕД (діапазон осередків).