行列式
または行列式、-数学では、正方形の表の形式の数値の記録であり、それに応じて別の数値が配置されます（行列式の「値」）。 多くの場合、「行列式」という用語は、行列式の意味とその表記法の形式の両方を意味します。 行列式を使用すると、たとえば、解析幾何学や数学的解析で線形方程式を解くときに発生する複雑な式を簡単に記述できます。 行列式の発見は、日本の数学者S. Kova（1683）と、独立してG. Leibniz（1693）に起因しています。 現代の理論は、19世紀初頭のJ. Binet、O。Cauchy、C。Jacobiの作品にまでさかのぼります。 最も単純な行列式は、要素と呼ばれる4つの数値で構成され、2行2列に配置されています。 このような行列式は2次であると言われています。 たとえば、これが決定要因です

その値は2*5〜3 * 1（つまり、10〜3または7）です。 一般的なケースでは、2次行列式は通常次の形式で記述されます

そして、その値はa1b2-a2b1です。ここで、aとbは数値または関数です。 3次行列式は、3行3列に配置された9つの要素で構成されます。 一般に、n次行列式はn2要素で構成され、通常は次のように記述されます。

各要素の最初のインデックスは行の番号を示し、2番目はこの要素が配置されている交差点の列の番号を示します。したがって、aijはi番目の行とj番目の列の要素です。 多くの場合、そのような行列式は|aij|と記述されます。 行列式を計算する方法の1つは、ほとんどの場合、高階行列式の計算に使用され、「マイナー」で拡張することです。 行列式の任意の要素に対応するマイナーは、この要素が立っている交点の行と列を削除することによって元の行列式から取得された、1未満の次数の行列式です。 たとえば、行列式の要素a2に対応するマイナー

要素の「代数的補数」はそのマイナーであり、要素が立っている交点の行番号と列番号の合計が偶数の場合はプラス記号で、奇数の場合はマイナス記号で取得されます。 上記の例では、要素a2は1列目と2行目にあります。 合計（1 + 2）は奇数であるため、要素a2の代数的補数は、マイナス記号を付けて、そのマイナーに等しくなります。

行列式の値は、任意の行（または任意の列）の要素とそれらの代数的補数の積の合計に等しくなります。 たとえば、行列式

最初の列に展開された形式は

2行目の展開は次の形式になります

各マイナーを計算し、それを係数で乗算することにより、両方の式が同じであることを簡単に確認できます。 行列式の値。 行列式の値の下で

n個の要素のすべての積の合計を理解するのが通例です。

この式では、数値1、2、ј、nのすべての順列j1、ј、jnに対して合計が実行され、順列が偶数の場合は項の前にプラス記号が付き、この順列が奇数の場合はマイナス記号が前に付きます。 。 そのような合計は正確にnになります！ メンバーの半分はプラス記号で、半分はマイナス記号で示されます。 各合計項には、行列式の各列と各行からの1つの項が含まれます。 この合計は、未成年者の行列式を拡張することによって得られる式と一致することが証明できます。
行列式のプロパティ。行列式の最も重要な特性の中で、次のことに言及します。 （i）任意の行（または任意の列）のすべての要素がゼロの場合、行列式の値もゼロです。

（ii）2つの行（または2つの列）の要素が等しいか比例している場合、行列式の値はゼロです。

（iii）行列式の値は、そのすべての行と列が交換された場合、つまり、変更されません。 最初の行を最初の列として、2番目の行を2番目の列として、というように記述します。 （この操作は転置と呼ばれます）。 例えば、

（iv）ある行（または列）の要素に、別の行（または列）の対応する要素に任意の係数を掛けても、行列式の値は変わりません。 次の例では、2番目の行の要素に-2を掛けて、最初の行の要素に追加します。

（v）2つの行（または2つの列）が交換されると、行列式は符号を変更します。

（vi）1つの行（または1つの列）のすべての要素に共通の因子が含まれている場合、この因子は行列式の符号から除外できます。

例。 次の4次行列式の値を計算します。

4行目を1行目に追加しましょう。

4番目の列から1番目の列を引きます。

3番目の列に3を掛け、4番目の列から減算します。

必要に応じて、行と列を入れ替えることができます。

4行目の要素で行列式を展開してみましょう。 この行の3つの要素はゼロに等しく、ゼロ以外の要素は3番目の列にあり、合計（3 + 4）が奇数であるため、その代数補数にはマイナス記号が付いています。 その結果、次のようになります。

マイナーは3行目の要素に分解できます。その要素の2つはゼロに等しく、ゼロ以外の要素は3番目の列にあります。 合計（3 + 3）は偶数であるため、前の等式を継続できます。

アプリケーション。 連立方程式を解く

最初の方程式にb2を掛け、2番目の方程式にb1を掛けてから、一方の方程式をもう一方の方程式から引くことで得られます。 これらの操作を行うことにより、

または

それから

行列式の助けを借りたそのような解の記録は、n個の未知数を持つn個の一次方程式のシステムを解く場合への一般化を可能にします。 各行列式はn次になります。 連立一次方程式の行列式

意思

D = 0の場合、方程式は一貫していないか、独立していないことに注意してください。 したがって、行列式Dの予備計算により、連立一次方程式が解けるかどうかを確認できます。
解析幾何学の決定要因。円錐曲線の一般式は、次のように表すことができます。

行列式

判別式と呼ばれます。 D = 0の場合、曲線は平行線または交差線のペア、または点に縮退します（円錐曲線も参照）。 別の例：点（バイパス-反時計回り）（x1、y1）、（x2、y2）、および（x3、y3）に頂点がある三角形Aの面積は次の式で与えられます

行列式と行列の接続。行列は、長方形のテーブルの形式の数値の配列の記録です。 行列式は正方行列に関連しています。 たとえば、行列式

A、B、およびСが正方行列の場合、| A | * | B | = |C|。
も参照してください代数は抽象的です。
ジャコビアン。 x = f（u、v）、y = g（u、v）が座標変換である場合、行列式

これは、この変換のヤコビアンまたはヤコビ行列式と呼ばれます。 ある時点でJが0に等しくない場合、その近傍で、変換方程式はuとvに関して一意に解かれ、xとyの関数として表されます。
数学分析を参照してください。

コリアーズ百科事典。 -開かれた社会. 2000 .

同義語:

他の辞書にある「行列式」を確認してください。

限定詞、限定詞、男性。 （本）。 1.何かを決定し、表現するもの。 2.何か（科学的）を決定する際の参照として役立つ本。 植物の識別。 きのこガイド。 3.で構成される表現......。 ウシャコフ一義辞典

-（行列式）n2の数から特定の規則に従ってコンパイルされた数式で、1次の代数方程式のシステムを解いて研究するために使用されます。 数nは、行列式の順序と呼ばれます。 したがって、2次の行列式... ビッグ百科事典辞書

ロシア語の同義語の識別子、ヘッセ行列式、小行列式、行列式辞書。 名詞限定詞、同義語の数：10自動限定詞（1）… 同義語辞書

行列式-（行列式）n2の数から特定の規則に従ってコンパイルされた数式で、1次の代数方程式のシステムを解いて研究するために使用されます。 数nは、行列式の順序と呼ばれます。 したがって、2次の行列式... グレートポリテクニック百科事典

限定詞、私、夫。 1. nを決定するためのデバイス、および一般的には、nを実行できるようにするためのデバイス。 正確に決定します。 発信者IDが記載された電話。 O.リズム。 2.何nを決定するときに参照するための本。 （専門家。）。 O.植物..。 Ozhegovの説明辞書

-正方行列の（行列式）A = || aij || 次数n、detA多項式… 物理百科事典

行列式---通信トピック、基本概念EN決定要因..。 技術翻訳者ハンドブック

この用語には他の意味があります。行列式（意味）を参照してください。 行列式（または行列式）は、線形代数の基本概念の1つです。 行列式は、正方行列の要素の多項式です（つまり、y ... Wikipedia

行列式-3.4.6修飾子（補助）：UDC補助クラスコード。 ソース … 辞書-規範的および技術的文書の用語の参考書

私; m。1.本。 何が決定されるかは、何によって決定されます。 音は速度の決定要因になる可能性があります。 時間の主な決定要因は、宇宙空間での太陽の動きです。 2.仕様 何を決定するためのガイド（本または表）......。 百科事典の辞書

本

• 果実と種子による木本植物の被子植物の鍵、SinitsynEvgenyMikhailovich。 行列式は2つの部分で構成されています。 最初の部分は属を識別するための表であり、2番目の部分は木本植物の被子植物の種を識別するための表を含みます...

· 行列式 平方 n次の行列A また n次行列式 代数和に等しい数と呼ばれる P！ それぞれが製品であるメンバー P行列要素は、特定の符号を持つ各行と各列から1つずつ取得されます。 行列式はまたはで示されます。

二次行列式次のように表される数値です。 . 例えば .

三次行列式三角形の法則（サラスの法則）に従って計算されます。

例. .

コメント。 実際には、3次行列式、および高次行列式は、行列式のプロパティを使用して計算されます。

n次行列式のプロパティ.

1.各行（列）が同じ番号の列（行）に置き換えられても、行列式の値は変更されません- 転置.

2.行列式の行（列）の1つがゼロで構成されている場合、行列式の値はゼロです。

3.行列式で2つの行（列）が入れ替わっている場合、行列式の絶対値は変更されず、符号は反対に変更されます。

4. 2つの同一の行（列）を含む行列式はゼロに等しくなります。

5.行（列）のすべての要素の公約数は、行列式の符号から取り除くことができます。

· マイナー 行列式のいくつかの要素 Pこの次数は行列式と呼ばれます（ P-1）-選択した要素が配置されている交差点の行と列を削除することにより、元の行から取得された次数。 指定：。

· 代数加算 行列式の要素はマイナーと呼ばれ、記号が付いています。 指定：だから =。

6.正方行列の行列式は、任意の行（または列）の要素とそれらの代数的補数（ 分解定理).

7.番目の行の各要素が合計である場合 k項の場合、行列式は合計として表されます k-番目の行を除くすべての行が元の行列式と同じであり、最初の行列式の-番目の行が最初の項で構成され、2番目の行が2番目の-で構成されている行列式。 同じことが列にも当てはまります。

8.数値を掛けた別の行（列）が行（列）の1つに追加されても、行列式は変更されません。

結果. 他の行（列）の線形結合が行列式の行（列）に追加された場合、行列式は変更されません。

9.対角行列の行列式は、主対角上の要素の積に等しくなります。

コメント。 三角行列の行列式も、主対角線上の要素の積に等しくなります。

リストされた行列式のプロパティにより、計算を大幅に簡素化できます。これは、高次の行列式にとって特に重要です。 この場合、変換された行列ができるだけ多くのゼロを含む行または列を持つように元の行列を変換することをお勧めします（行または列を「ゼロ化」する）。

例。行列式のプロパティを使用して、前の例で指定された行列式を再度計算します。

解決：最初の行には共通因子-2があり、2番目の行には共通因子3があることに注意してください（プロパティ5による）。 次に、プロパティ6（拡張定理）を使用して、たとえば最初の列で行列式を拡張します。

最も効果的な 行列式を対角または三角形に縮小する方法 。 行列式を計算するには、行列式を変更せず、行列式を対角線に変換できる行列式の変換を実行するだけで十分です。

結論として、正方行列の行列式がゼロに等しい場合、その行列は次のように呼ばれることに注意してください。 退化 （または特別） , それ以外は - 非縮退 .

1.行列式は転置中に変化しません。

2.行列式の行の1つがゼロで構成されている場合、行列式はゼロに等しくなります。

3.行列式で2つの行が再配置されると、行列式の符号が変わります。

4.2つの同一の文字列を含む行列式はゼロに等しくなります。

5.行列式のある行のすべての要素に、ある数kを掛けると、行列式自体にkが掛けられます。

6.2つの比例行を含む行列式はゼロに等しくなります。

7.行列式のi番目の行のすべての要素が、2つの項aij = bj + cj（j =）の合計として表される場合、行列式は、行列式の合計に等しくなります。 i番目の行の場合、は与えられた行列式と同じであり、一方の被加数のi番目の行は要素bjで構成され、もう一方の行は要素cjで構成されます。

8.別の行の対応する要素に同じ数を掛けたものが、その行の1つの要素に追加されても、行列式は変更されません。

コメント。行の代わりに列が使用される場合、すべてのプロパティは有効なままです。

マイナー n次の行列式dの要素aijのMijは、この要素を含む行と列を削除することによってdから取得される次数n-1の行列式です。

代数加算行列式dの要素aijは、そのマイナーM i jであり、符号（-1）i+jを取ります。 要素aijの代数的補数は、Aijで表されます。 したがって、A i j =（-1）i + j Mij。

次数nの行列式を低次の行列式で表すことができるという事実に基づいて、行列式を実際に計算する方法は、次の定理によって与えられます。

定理 （行または列の行列式の分解）。

行列式は、任意の行（または列）のすべての要素とそれらの代数的補数の積の合計に等しくなります。 言い換えると、i番目の行の要素に関してdの分解がありますd = a i 1 A i 1 + a i 2 A i 2 + ... + a i n A i n（i =）

またはj番目の列d=a 1 j A 1 j + a 2 j A 2 j + ... + a n j A n j（j =）。

特に、1つを除く行（または列）のすべての要素がゼロに等しい場合、行列式はこの要素に代数の補数を掛けたものに等しくなります。

例1.4。行列式を計算しない 、ゼロに等しいことを示します。 解決。 2番目の行から最初の行を引くと、行列式が得られます オリジナルと同じです。 3番目の行から最初の行も減算すると、行列式が得られます 、2つの行は比例しています。 この行列式はゼロです。

例1.5。行列式を計算するD= 、2列目の要素で展開します。

解決。 2番目の列の要素によって行列式を展開してみましょう。

D = a 12 A 12 + a 22 A 22 + a 32 A 32 =

例1.6。行列式を計算する

A =
、主対角線の片側のすべての要素がゼロに等しい。 解決。最初の行の行列式Aを展開してみましょう：A = a 11 A 11 = 。 右側の行列式は、最初の行に沿って再度展開できます。次のようになります。

A =
。等。 nステップ後、等式A = a 11 a 22 ...annに到達します。

3.連立一次方程式の基本概念。 クラマーの定理。

意味. 連立一次方程式の結合です nそれぞれが含まれている線形方程式 k変数。 それはこのように書かれています：

多くの人は、初めてより高い代数に直面したとき、方程式の数は変数の数と必ず一致しなければならないと誤って信じています。 学校の代数ではこれが通常当てはまりますが、高等代数の場合、これは一般的に言えば真実ではありません。

意味. 連立方程式を解く数列です（ k 1 ,k 2 , ..., k n）、これはシステムの各方程式の解です。 変数の代わりにこの方程式に代入する場合 バツ 1 , バツ 2 , ..., x n正しい数値を示します。

それぞれ、 連立方程式を解くすべてのソリューションのセットを見つけるか、このセットが空であることを証明することを意味します。 方程式の数と未知数の数は同じではない可能性があるため、次の3つのケースが考えられます。

1.システムに一貫性がない、つまり すべてのソリューションのセットは空です。 システムを解決する方法に関係なく、簡単に検出できる非常にまれなケース。

2.システムは一貫性があり、定義されています。 解決策は1つだけです。 学校からよく知られているクラシックバージョン。

3.システムは互換性があり、定義されていません。 無限に多くのソリューションがあります。 これは最も難しいオプションです。 「システムには無限のソリューションのセットがある」と述べるだけでは不十分です。このセットがどのように配置されているかを説明する必要があります。

意味。 変数 x iと呼ばれる 許可、システムの1つの方程式にのみ含まれ、係数が1の場合、言い換えると、残りの方程式では、変数の係数 x iゼロに等しい必要があります。

各方程式で許可された変数を1つ選択すると、連立方程式全体で許可された変数のセットが得られます。 この形式で記述されたシステム自体も、許可されたと呼ばれます。 一般的に言って、同じ初期システムを異なる許可されたシステムに減らすことができますが、これは今のところ私たちには関係ありません。 許可されているシステムの例は次のとおりです。

変数に関しては両方のシステムが許可されます バツ 1 , バツ 3と バツ 4。 ただし、同じ成功を収めると、2番目のシステムは比較的許可されていると主張できます。 バツ 1 , バツ 3と バツ五 。 最後の方程式を次のように書き直すだけで十分です。 バツ 5 = バツ 4 .

ここで、より一般的なケースを考えてみましょう。 すべてを手に入れましょう k変数、そのうち r許可されています。 次に、2つのケースが考えられます。

1.許可される変数の数 r変数の総数に等しい k: r = k。 システムは k方程式 r = k許可された変数。 このようなシステムは協調的で明確です。 バツ 1 = b 1 , バツ 2 = b 2 , ..., Xのk = b k;

2.許可される変数の数 r変数の総数より少ない k: r < k。 残り （ k − r）変数は無料と呼ばれます-許可された変数を簡単に計算できる任意の値を取ることができます。

したがって、上記のシステムでは、変数 バツ 2 , バツ 5 , バツ 6（最初のシステムの場合）および バツ 2 , バツ 5（2番目）は無料です。 自由変数がある場合は、定理としてより適切に定式化されます。

の解き方？： –置換法（「学校法」）を使用して連立一次方程式を解きます。
–システム方程式の項ごとの加算（減算）によるシステムの解法。
–Cramerの公式によるシステムの解法。
–逆行列を使用したシステムの解。
–ガウス法によるシステムの解法。

クレイマー

まず、2つの未知数を持つ2つの線形方程式のシステムに対するクラメルの公式を考えます。 2つの変数を持つ線形方程式のシステムがあり、クラメルの法則に従って正確に解くことをお勧めします。

連立方程式を考えてみましょう

最初のステップでは、行列式を計算します。これは次のように呼ばれます。 システムの主な決定要因.

の場合、システムには無限に多くのソリューションがあるか、一貫性がありません（ソリューションがありません）。 この場合、クラメルの公式は役に立ちません。使用する必要があります ガウス法.

の場合、システムには一意の解があり、根を見つけるには、さらに2つの行列式を計算する必要があります。

実際には、上記の修飾子はラテン文字で表すこともできます。

方程式の根は次の式で求められます：、

例7

連立一次方程式を解く

方程式の係数が非常に大きく、右側にコンマ付きの小数があります。 数学の実際のタスクでは、コンマはかなりまれなゲストです。私はこのシステムを計量経済学の問題から取り入れました。

そのようなシステムをどのように解決するのですか？ ある変数を別の変数で表現することもできますが、この場合、非常に不便なひどい派手な分数が確実に得られ、ソリューションの設計はひどいものになります。 2番目の方程式に6を掛け、項を項ごとに引くことができますが、同じ分数がここに表示されます。

何をすべきか？ そのような場合、Cramerの公式が助けになります。

そのため、システムには独自のソリューションがあります。

;

;

ご覧のとおり、ルーツは不合理であることが判明し、ほぼ発見されました。これは、計量​​経済学の問題には非常に受け入れられます（そしてありふれたことですらあります）。

タスクは既製の式に従って解決されるため、ここではコメントは必要ありませんが、注意点が1つあります。 この方法を使用する場合、 義務割り当てのフラグメントは、次のフラグメントです。 « 、システムには独自のソリューションがあります 。 そうしないと、レビュー担当者がCramerの定理を軽視したことであなたを罰する可能性があります。

計算機で実行すると便利なチェックは不要ではありません。システムの各方程式の左側に近似値\u200b\u200binを代入します。 結果として、小さな誤差で、右側の数値を取得する必要があります。

クレイマーの公式

クラメルの方法は、次々と見つけることです。 マスターシステム識別子（5.3）、すなわち 行列式

と n補助行列式 D i（i =）。これは、i番目の列を自由なメンバーの列に置き換えることによって行列式Dから取得されます。

Cramerの式の形式は次のとおりです。

D×xi= D i（i =）。 （5.4）

（5.4）から、クラメルの公式が続きます。これは、システム（5.3）の互換性の質問に対する徹底的な答えを与えます。システムの主な行列式がゼロ以外の場合、システムは次の式で決定される一意の解を持ちます。

システムDの主行列式とすべての補助行列式Di= 0（i =）の場合、システムには無限の数の解があります。 システムの主行列式D=0であり、少なくとも1つの補助行列式がゼロと異なる場合、システムは不整合です。

例1.14。 クラメルの方法を使用して連立方程式を解きます。

x 1 + x 2 + x 3 + x 4 = 5、x 1 + 2x 2-x 3 + 4x 4 = -2、2x 1-3x 2-x 3-5x 4 = -2、3x 1 + x 2 + 2x3 + 11x4=0。

解決。このシステムの主な決定要因D= =-142¹0なので、システムには独自のソリューションがあります。 行列式Dから得られる補助行列式Di（i =）を、xiの係数で構成される列を自由なメンバーの列に置き換えることによって計算してみましょう。D1= = --142、D 2 = = --284、D 3 = = - 426,

D4 = =142。したがって、x 1 = D 1 / D = 1、x 2 = D 2 / D = 2、x 3 = D 3 / D = 3、x 4 = D 4 / D = -1、システムの解ベクトルC=（1、2、3、-1）Tです。

連立一次方程式の基本概念。 ガウスの方法。

上記を参照。

ガウスの消去法（未知数を完全に排除する方法）-線形代数方程式の二乗システムを解く、行列の逆行列を見つける、与えられた基底のベクトルの座標を見つける、または行列の階数を見つけるために使用される方法。 この方法は、ガウスの方法を修正したものです。

アルゴリズム

1.少なくとも1つのゼロ以外の値を持つ行列の最初の左の列を選択します。

2.この列の一番上の数値がゼロの場合は、マトリックスの最初の行全体を、この列にゼロがないマトリックスの別の行に変更します。

3.最初の行のすべての要素は、選択した列の一番上の要素で分割されます。

4.残りの行から、最初の行を減算し、対応する行の最初の要素を掛けて、各行の最初の要素（最初の行を除く）をゼロにします。

6.この手順を1回繰り返すと、上三角行列が得られます

7.最後から2番目の行から最後の行を引き、対応する係数を掛けて、主対角線上の1つだけが最後から2番目の行に残るようにします。

8.後続の行について、前の手順を繰り返します。 その結果、単位行列と自由ベクトルの代わりの解が得られます（それを使用してすべて同じ変換を実行する必要があります）。

9.逆行列を取得するには、すべての操作を同じ順序で単位行列に適用する必要があります。

ガウス法

歴史的に、線形方程式のシステムを解くための最初の最も一般的な方法は、ガウス法、または未知数を連続的に除去する方法です。 この方法の本質は、未知数を連続的に除去することにより、与えられたシステムが与えられたものと同等の階段状（特に三角形）のシステムに変換されるという事実にあります。 ガウス法による線形連立方程式の実際の解法では、連立方程式自体ではなく、このシステムの拡張行列に縮小して、行に対して基本変換を実行する方が便利です。 変換中に連続して取得される行列は、通常、等価記号で接続されます。

例1.13. ガウスの方法を使用して連立方程式を解きます：x + y-3z = 2、3x-2y + z =-1、2x + y-2z=0。

解決。このシステムの拡大行列を記述します

そして、その行に対して次の基本変換を実行します。a）2番目と3番目の行から最初の行を減算し、それぞれ3と2を掛けます。 ~ ;

b）3番目の行に（-5）を掛けて、2番目の行を追加します。 .

これらすべての変換の結果として、このシステムは三角形の形式に縮小されます：x + y-3z = 2、-5y + 10z = -7、-10z=13。

最後の方程式から、z=-1.3がわかります。 この値を2番目の式に代入すると、y=-1.2になります。 最初の方程式からさらに、x=-0.7が得られます。

ノートブックから:

ガウス法

この方法は、順方向と逆方向の2つの部分で構成されます。

直接的な動きは、基本行変換の助けを借りて、SLE行列を段階的な形式に拡張する動作で構成されます。 ステップマトリックスでは、後続の各行の先頭に、前の行よりも多くのゼロがあります-またはゼロです

例：

行列行の基本変換は次のとおりです。

1）行列の1つの行の数値にいくつかの数値を掛けて、行列の下位の行の1つに加算します。

2）場所を変えて2行

ガウスの方法の逆の動きは、下のゼロ行から開始して、他の変数に関していくつかの変数を順次表現することで構成されます。 結果は一般的な解決策です。

前進ストロークの後、展開されたマトリックスのステップタイプには3つのオプションがあります。

1）次の各行の先頭には、前の行よりも正確に1つ以上のゼロがあります。

例：

方程式を1行ずつ記述し、一番下の行から変数の値を見つけ始めます。

4X4\u003d8ÞX4\u003d 2

前の式に代入します

2X 3 -3X 4 \ u003d -8つまり、 2X 3 -3 * 2 \u003d-8または2X3\ u003d -2、ÞX 3 \ u003d -1、2行目のX3とX4を置き換えます。 SLUの唯一のソリューションを取得します

2）ゼロ以外の行の数が変数の数より少ない。 次に、行の1つに、前の行より少なくとも2つ多い最初のゼロが含まれ、後続の非ゼロ行は、数値b = 0の形式（0 ... 0 b）ではないと見なされます。

例えば：

3）最後の非ゼロ行は（0…0 / b）の形式になります。ここで、b = 0は、矛盾する等式o = bに対応するため、システムに互換性がありません。

ガウス法によるSLEの解法

2X 1 + 3X 2 + X 3 \ u003d 1

4X 1 + 5X 2 + 4X 3 = 7

6X 1 + 10X 2 -3X 3 = -10

直接移動の拡張行列を作成します。

行列式の計算 n-次数：

行列式の概念 n-次数

行列式に関するこの記事を使用すると、次のような問題を解決する方法を確実に学ぶことができます。

方程式を解きます：

そして、教師がとても思いつくのが大好きな他の多くの人たち。

行列式または単に行列式は、連立一次方程式を解く上で重要な役割を果たします。 一般に、行列式はこの目的のために発明されました。 「行列式」とも言われることが多いので、ここでも行列式について触れておきます。 マトリックスは、交換できない数字で構成された長方形のテーブルです。 正方行列は、同じ数の行と列を持つテーブルです。 行列式を持つことができるのは正方行列だけです.

次のスキームに従って行列式を書く論理を理解するのは簡単です。 学校でおなじみの2つの未知数を持つ2つの方程式のシステムを考えてみましょう。

行列式では、未知数の係数が順番に書き込まれます。最初の行（最初の方程式から）、2番目の行（2番目の方程式から）：

たとえば、連立方程式が与えられた場合

次に、未知数の係数から次の行列式が形成されます。

それで、私たちがに配置された数字で構成される正方形のテーブルを与えられたとしましょう n行（水平行）および n列（垂直行）。 これらの番号の助けを借りて、私たちが以下で研究するいくつかの規則に従って、彼らは彼らが呼ぶ番号を見つけます 行列式 n次のように示されます。

(1)

番号は呼ばれます 要素行列式（1）（最初のインデックスは行の番号を意味し、2番目のインデックスは要素が交差する列の番号を意味します。 私 = 1, 2, ..., n; j= 1、2、...、n）。 行列式の順序は、その行と列の数です。

両方のインデックスが同じである行列式の要素を結ぶ架空の直線。 要素

と呼ばれる 主対角線、もう一方の対角線は 側.

2次および3次行列式の計算

最初の3つの次数の行列式がどのように計算されるかを示しましょう。

一次行列式は要素自体です。

2次行列式は、次のように取得された数です。

, (2)

それぞれ主対角線と副対角線上の要素の積。

等式（2）は、主対角線の要素の積がその符号で取得され、2次対角線の要素の積が反対の符号で取得されることを示しています。 .

例1二次行列式を計算します。

解決。 式（2）により、次のことがわかります。

3次行列式は、次のように取得された数値です。

(3)

この式を覚えるのは難しいです。 ただし、という単純なルールがあります 三角形のルール 、表現を再現しやすくします（3）。 行列式の要素を点で示し、行列式の要素の積を与えるそれらの要素を線分で接続します（図1）。

式（3）は、主対角線の要素と、それに平行な底辺を持つ2つの三角形の頂点にある要素の積がそれらの符号で取得されることを示しています。 反対のものと-二次対角線の要素の積、およびそれに平行な2つの三角形の頂点にある要素 .

図1では、主対角線とそれに対応する三角形の底辺、および側面の対角線とそれに対応する三角形の底辺が赤で強調表示されています。

決定要因を計算するときは、高校のように、マイナスの数にマイナスの数を掛けるとプラス記号になり、プラス記号にマイナスの数を掛けるとマイナス記号の付いた数になることを覚えておくことが非常に重要です。

例2 3次行列式を計算します。

解決。 三角形のルールを使用して、次のようになります。

行列式の計算 n-次数

行列式の行または列の展開

行列式を計算するには n次の定理を知って使用する必要があります。

ラプラスの定理。行列式は、任意の行の要素とそれらの代数的補数の積の合計に等しくなります。

意味。 行列式の場合 n順序は任意に選択します p行と p列（ p < n）、これらの行と列の交点にある要素が順序行列を形成します。

この行列式は次のように呼ばれます マイナー 元の行列式。 たとえば、行列式について考えてみます。

偶数の行と列から行列を作成しましょう。

行列式

と呼ばれる マイナー行列式。 2番目の注文のマイナーを受け取りました。 一次、二次、三次の様々な未成年者がから構築できることは明らかです。

要素を取り、それが行列式にある交差点で行と列を消すと、要素の小行列式と呼ばれる小行列式が得られます。これは次のように表されます。

.

マイナーにを掛けると、3 + 2は要素が交差する行と列の番号の合計であり、結果の積は次のように呼び出されます。 代数加算要素であり、で表されます。

一般に、要素の小行列式は、で示され、代数補数は、で示されます。

(4)

たとえば、要素の代数的補数と3次行列式を計算してみましょう。

式（4）により、次のようになります。

行列式を分解するとき、行列式の次のプロパティがよく使用されます n-次数：

別の行または列の対応する要素と定数係数の積が任意の行または列の要素に追加された場合、行列式の値は変更されません。

例4

1行目と3行目から4行目の要素を事前に減算すると、次のようになります。

得られた行列式の4列目では、3つの要素がゼロです。 したがって、最初の3つの積がゼロになるため、この行列式を4番目の列の要素で拡張する方が収益性が高くなります。 それが理由です

あなたはで解決策をチェックすることができます オンラインの行列式計算機 .

次の例は、任意の（この場合は4番目の）行列式の計算を2次行列式の計算に減らす方法を示しています。

例5行列式を計算します。

3番目の行から最初の行の要素を減算し、最初の行の要素を4番目の行の要素に加算すると、次のようになります。

最初の列では、最初の要素を除くすべての要素がゼロです。 つまり、行列式は最初の列ですでに分解できます。 しかし、実際には3次行列式を計算したくありません。 したがって、さらに変換を行います。3番目の行の要素に2番目の行の要素を加算し、2を掛け、4番目の行の要素から2番目の行の要素を減算します。 その結果、代数の補数である行列式自体を最初の列で展開できます。2次行列式を計算するだけで、記号に混乱することはありません。

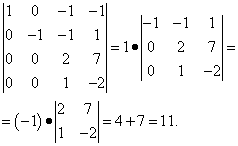
行列式を三角形の形にする

対角線の1つの片側にあるすべての要素がゼロに等しい行列式は、三角形と呼ばれます。 行または列の順序を逆にすることにより、2次対角の場合が1次対角の場合に縮小されます。 このような行列式は、主対角線の要素の積に等しくなります。

三角形に縮小するには、行列式の同じプロパティが使用されます n前の段落で使用した次数：別の行または列の対応する要素の積を定数係数で任意の行または列の要素に追加すると、行列式の値は変更されません。

あなたはで解決策をチェックすることができます オンラインの行列式計算機 .

行列式のプロパティ n-次数

前の2つの段落では、行列式のプロパティの1つをすでに使用しています。 n-次数。 場合によっては、行列式の計算を簡略化するために、行列式の他の重要なプロパティを使用できます。 たとえば、行列式を2つの行列式の合計に減らすことができ、その一方または両方を行または列に沿って便利に拡張できます。 このような単純化のケースはたくさんあり、行列式のいずれかのプロパティを使用するかどうかの問題は、個別に決定する必要があります。

行列式 (行列式）は、数値または数学記号の正方形の表です（ Δd).

意味。 行列式 n×n数です：

どこ （ α1、α2、...、αn）-からの数の順列 1 前 n, N（α1、α2、..。、αn）-順列の反転の数、合計は、順序のすべての可能な順列で発生します n.

行列式 A基本的には de t（A）、| A |、 また ？（A）.

すべてのタイプの代数行列の解が見つかるパラメータ。

に 行列式を見つける行列を解くときは、行列の基本的な性質と一連のアクションを知る必要があります。

1. 次数の行列の場合 n = 2行列式は、次の式を使用して求められます。 Δ= a11 *22-12 *21
2. 次数の行列の場合 n = 3行列式は、代数の加算またはSarrusの方法を使用して検出されます。
3. 次元が3を超える行列は、代数の加算に分解され、その行列式（マイナー）が検出されます。 たとえば、4次行列の行列式は、行または列の展開によって計算されます。

ために 行列式を見つける、マトリックスに関数が含まれている場合、標準の方法が使用されます。 たとえば、3次の行列の行列式を見つけるには：

最初の行の展開を使用してみましょう：

Δ=sin（x）×+1×=2sin（x）cos（x）-2cos（x）= sin（2x）-2cos（x）

行列式を計算します。

行列式を計算する以下にリストされているいくつかの方法があります。

行列の行列式を計算する最も一般的な方法は、代数的な加算を選択する方法です。 この方法には、より単純なバージョンがあります。Sarrusルールを使用した行列式の計算です。 これらの方法は、単純な小さな行列の行列式を計算する場合とは異なります。大きな次元の行列を計算する必要がある場合は、次のようになります。 行列式の計算方法:

• 次数削減法による行列式の計算、
• ガウス法による行列式の計算（行列を三角形に縮小することによる）、
• 分解法による行列式の計算。

Excelでは、行列式を計算するために、関数= MOPRED（セルの範囲）が使用されます。